设置大问题——由“教师讲”转变为“学生悟”——“因式分解的平方差公式”的教学

◎哈尔滨市香坊区教师进修学校 李 杰

设置大问题
——由“教师讲”转变为“学生悟”——“因式分解的平方差公式”的教学

◎哈尔滨市香坊区教师进修学校 李 杰

一、主题与背景

这节课是2014年哈尔滨市第五届“烛光杯”课堂教学大赛的课题.其中有五位教师同时讲这个课题.因式分解的平方差公式（以下简称公式）：a2-b2=（a+b）（a-b），是在学习整式乘法的平方差公式（a+b）（a-b）=a2-b2之后学习的.这一节课的重点是让学生掌握公式的特点，并能熟练地运用公式进行一个多项式的因式分解.在这个过程中，体会整式乘法与因式分解的关系.在日常的教学中，绝大多数的教师进行这节课的教学时，一般都是直接给出公式，讲清公式的特点，例题示范后，进行大量的多项式因式分解的训练.这样的教学，从表面上看，学生顺利地掌握了公式，轻松应对中考.深度思考后会发现，学生虽然能熟练应用公式进行因式分解，但他们不一定体会到公式的来龙去脉和其中蕴含的数学思想方法，真正感悟公式的特点，是教师“教会”而不是自主“学会”公式的应用.那么对于这类公式课型的教学，除了应对中考，学生思维能力会有哪些提高呢？如何通过设计大问题情境，由“教师讲”转变为“学生悟”呢？

为此，在初中数学学科的教研实践基地旭东中学，由两位初中数学教研员、旭东中学校长、主任及数学组全体教师组成课题组，讲课教师确定为于立波老师，以因式分解的平方差公式为例，进行了专题研究.

二、情景与描述

本节课我们通过“公式的得出、公式的辨析、公式的应用”三个主要环节进行描述.

环节一：公式的得出

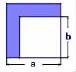
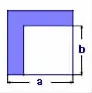
问题一：有一个边长为5的大正方形和一个边长为4的小正方形，这样叠合在一起，那么阴影部分的面积是多少？

生：9.

师：反应真快！

问题二：如果大正方形的边长是10，小正方形的边长是6，那么阴影部分的面积又是多少？

生：64.

师：好！

问题三：如果大正方形的边长是5.6，小正方形的边长是4.6，那么阴影部分的面积又是多少？

（学生思考片刻，有些困难.）

师：看样子这样的算式快速算出有些困难，有没有更好的简便方法计算呢？我们继续研究.

师：如果大正方形的边长是a，小正方形的边长是b，阴影的面积是多少？

生：a2-b2.

问题四：你还能用其他形式表示阴影部

分的面积吗？

（同桌为一个小组，利用学具合作完

成，完成后汇报.）

教师提供方便快捷的图形学具，各小组同学积极思考，相互合作，研究出几种不同形式，教师深入其中，适时指导.各组学生汇报成果：

组1：将阴影部分分割成两个长方形，然后拼成一个大长方形，从而得到阴影部分的面积（a+b）（a-b）.

组2：将阴影部分分割成两个长方形和一个小正方形，得到阴影部分的面积（a-b）2+2b（a-b），整理后得（a+b）（a-b）.

组3：将阴影部分分割成两个直角梯形的方式，可能得到阴影部分的面积.整理后得

师：分割得很巧妙，真是不错的想法.

师：我们来看，不管哪个式子表示的都是阴影的面积，那么它们在数量上应该怎么样？

生：相等.

师：这样a2-b2=（a+b）（a-b），我们在哪儿见过类似的式子？

生：在学整式乘法时学习了（a+b）（a-b）=a2-b2平方差公式.

师：实质上我们把整式乘法的平方差公式等号两边互换位置就得到了a2-b2=（a+b）（a-b）．

师：观察这个等式，从右到左是整式乘法，那么从左到右是什么呢？

生：因式分解.

师：这就是我们这节课所研究的因式分解的平方差公式，用这一公式将一个多项式因式分解的方法就

是我们今天将要研究的公式法.

（板书：21.3.2公式法（1））

环节二：公式的辨析

师：请同学们观察公式的特点，谁能尝试用语言描述一下这个公式.

（几个学生描述，教师板书.）

师：我们再来看前边的问题，大正方形的边长是5.6，小正方形的边长是4.6，那么阴影部分的面积如何求呢？

生：5.62-4.62=（5.6+4.6）×（5.6-4.6）=10.2.

师：同学们很智慧啊，用我们今天学习的因式分解的平方差公式就能快速计算出结果了！

问题一：在材料纸上写两个能用平方差公式因式分解的多项式，并且同桌交流一下，说说你写的多项式为什么能用平方差公式因式分解？

片刻之后，学生纷纷回答：①x2-9；②4x2-9y2；③（x-m）2-（x+n）2；④3x2-7y2.

学生充分交流后，教师引导学生找出典型例子，学生到黑板上讲解.之后教师又拿出几个多项式：

问题二：x2+y2、-x2+y2、-x2-y2，大家看这些多项式能不能用平方差公式因式分解呢？为什么？在这个过程中，应该注意什么？

师：大家辨析得非常好，那么怎样的多项式才能用平方差公式因式分解，谁能提醒同学应该关注什么？

在学生热烈的研讨下，大家基本达成共识：应用平方差公式因式分解的多项式，主要应该有两项，有平方，还有差的形式，两项异号.更可贵的是，一名学生发言中强调：为了不出错，首先把前后两项分别写成整体平方的形式，确定谁相当于公式中的a，谁相当于公式中的b，然后再进行因式分解.这些都是由学生探究发现的，是非常难得的.

环节三：公式的应用

教师设计一个很有思维含量的问题.

问题：从下列式子中：y4、-ab、x4、1、16x2、a3b，选取两个式子组成一个多项式，并因式分解.与同桌同学合作完成.

在学生交流中，学生组合成很多的多项式，并进行因式分解，教师选择几个典型的多项式：x4-y4；x4-16x2；a3b-ab.学生到黑板上板书并讲解.学生发现一些典型错误，有的没有分解到最后，学生之间大胆纠错，相互质疑.最后归纳由学生进行一个多项式因式分解时，易错点和注意事项.

三、问题与讨论

关于“公式的得出”环节，在备课时，大家争论的焦点在：方案一，一部分教师认为，因式分解的平方差公式a2-b2=（a+b）（a-b），实质上可以直接由整式乘法的平方差公式（a+b）（a-b）=a2-b2等号左右两端交换位置得到，我们教学时，可以直接得到，这样简洁直观，一目了然.方案二，另一部分教师则坚持，由学生感兴趣的两个正方形叠合在一起，（如下图）快速回答剩余部分的面积入手，从特殊情况边长是数字入手，再过渡到一般，从图形的角度来验证公式.这样操作虽然需要一定的时间，但是这样能很好地渗透数形结合的思想，引导学生用几何的方式解决代数的问题.

究竟怎样做才是有利于学生思维发展呢？大家展开了深入的讨论，用图形的面积来验证公式是否必要？其中A教师的发言引起大家的深思，用方案二不仅仅是从图形的角度验证公式，它还有一个重要功能，是让学生体会学习因式分解平方差公式的重要性，也就是我们为什么要学习这个公式，这样学生会对本节课产生浓厚的兴趣，所以，方案二是可取的.教师B又有不同的观点，方案二的作用是明显的，但它不能让学生更好地感悟整式乘法与因式分解之间的关系.真理越辩越明，最后，达成了共识.首先通过几组正方形图片叠合，求剩余部分的面积作为热身，在数据上由简单到复杂的过程中，产生认知冲突，然后设置大问题：利用学具探究正方形边长为a、b时，叠合后剩余部分的面积，从而，从图形的角度得到了a2-b2=（a+b）（a-b），然后应用它解决刚才产生认知冲突的问题，即5.62-4.62,如何计算的问题，让学生充分感受到新知学习的必要性，再自然联想到前面学习过的整式乘法的平方差公式（a+ b）（a-b）=a2-b2，将它左右两边交换位置，也可以得到因式分解的平方差公式a2-b2=（a+b）（a-b）.

这样的设计既让学生有浓厚的兴趣的同时，还使数与形结合得更紧密，同时又自然地体现了整式乘法与因式分解的关联.

关于“公式的辨析”及“公式的应用”环节，第一次上课的设计是先引导学生观察公式的特点，再尝试用语言叙述出来，为了进一步体会具体问题中的式子与公式中a、b的对应性，教师举两个简单的例子作示范，说明如何与公式中的a、b对应，并讲解正规的书写格式，然后给出例二，复杂多项式的因式分解（需两次分解的多项式），引导学生总结易错点.课后，听课教师在讨论中一致认为，观察公式的特点、用语言描述公式是非常必要的，可以加深对公式的理解，关于具体问题中的多项式与公式中a、b的对应性的理解，是学生熟练准确应用公式的关键所在，课上老师这样示范，学生会模仿照做，从应试角度看，解决简单多项式的因式分解没有问题，但是突出表现教师牵制学生来思考它们的对应性，那么如何引导学生自己感悟从不同角度辨析公式呢？还有对公式的应用大家也有不同的看法：问题不应该由教师直接给出，易错点也不应以教师为主强调，应让学生悟出.问题出在课堂设置的问题太小、太碎，缺少思维空间.经过大家的研究，对第一次上课的问

题设置修改为最后一次上课的方案.

四、诠释与研究

按照研究的方案进行教学后，课题组成员再一次进行了反思.在课堂的关键环节的问题设置，如：问题四：你还能用其他形式表示阴影部分的面积吗？（两名同学为一个小组，利用学具合作完成，完成后汇报.）问题一：在材料纸上写两个能用平方差公式因式分解的多项式，并且同桌交流一下，说说你写的多项式为什么能用平方差公式因式分解？问题二：x2+y2、-x2+y2、-x2-y2，大家看这些多项式能不能用平方差公式因式分解呢？为什么？在这个过程中，应该注意什么？问题：从下列式子中：y4、-ab、x4、1、16x2、a3b，选取两个式子组成一个多项式，并因式分解，小组合作完成.这些问题具有以下特点：其一直接指向本节课的本质，其二这些问题都需要学生动脑思考、动手操作及相互合作再能完成，思维含量较大.而教师在课堂上组织学生解决问题策略恰当，给学生自主感悟公式与熟练掌握公式提供了足够的时间和空间.在思维发展的关键点上，恰当地采取合作学习，学生在倾听、思考、合作、质疑中感悟新知，收获新知.

同时我们也发现，在设置大问题，放手让学生解决问题的过程中，教师的引导作用和关键环节的掌控至关重要.如：在学生用图形探究公式和利用学具操作遇到困难时，教师不应该袖手旁观，应及时指导学生使用学具，把握课堂节奏，减少不必要的时间浪费，在公式的应用环节中，学生自主发现纠错因式分解易错点时，同样也需要教师及时提升.课堂设置问题越大、越开放，课堂生成对教师来说要求就越高，需要教师反应机敏，处事灵活，及时调控，这也是教学机智的充分体现.

对于这样代数公式类课型的教学，让学生熟练掌握公式的同时，应引导学生经历公式的生成过程，在此过程中，注意渗透数学思想方法，积累必要的数学活动经验.教会学生自主感悟公式，学会熟练应用公式，寻找易混易错点，给学生更多的思考空间.从而提高学生发现问题、提出问题、分析问题与解决问题的能力.

E-mail:88686329@qq.com

❖编辑/张烨