压水堆燃料棒裂变产物释放产生比计算方法

许 锐 董 冰 付亚茹 梅其良 王德忠

压水堆燃料棒裂变产物释放产生比计算方法

许 锐1董 冰1付亚茹2梅其良2王德忠1

1（上海交通大学 上海 200240）2（上海核工程研究设计院 上海 200233）

为对压水堆一回路源项进行准确分析，在研究了美国核管制委员会(Nuclear Regulatory Commission, NRC)发布的计算气体裂变产物释放产生比(Release to Birth Ratio, R/B)的ANSI/ANS-5.4标准及法国METEOR 1.5程序计算气体裂变产物释放产生比的方法后，分别利用几种方法计算了燃料棒在不同功率水平以及不同燃耗下的几种气体裂变产物的释放产生比，对几种方法进行了研究分析。结果表明，燃料棒的裂变产物释放产生比会随着其功率以及燃耗而增大，相较于美国ANSI/ANS-5.4-2011标准，法国METEOR 1.5程序方法更为保守，而NRC原有的ANSI/ANS-5.4-1982标准最为保守，计算出的释放产生比最大，ANSI/ANS-5.4-2011标准能较好地适用于压水堆核电站裂变产物释放份额的计算。

燃料棒，裂变产物，释放产生比，ANSI/ANS-5.4标准，METEOR 1.5程序方法

反应堆在运行过程中燃料芯块会释放出大量的裂变产物到燃料芯块与包壳的间隙之中，当包壳发生破损时这些裂变产物又会通过包壳释放到一回路冷却剂中，释放到一回路冷却剂中的裂变产物成为核电厂的主要源项。这些裂变产物按其挥发性的差异可分为气体裂变产物(主要为Kr、I、Xe等惰性气体和卤素)、半挥发性裂变产物(Ba、Ru、Sr等)和难挥发性裂变产物(Rh、Pd、Tc等)[1]，由于气体裂变产物较易释放，因而在进行源项分析时考虑的主要是气体裂变产物。在分析核材料裂变生成的气体放射性核素时，尤需关注的是释放率的问题[2]。裂变产物的释放产生比(Release to Birth Ratio, R/B)是某种裂变产物从燃料芯块中释放到燃料芯块与包壳间隙的释放量与芯块产生的该种裂变产物产生量之比，其值的大小决定了裂变产物从燃料芯块释放到芯块与包壳间隙中的多少，对其进行准确计算对确定核电厂一回路源项具有重要意义。目前美国、法国等核电发达国家提出了多种计算裂变产物释放产生比的方法，这些方法计算出的结果大多较保守，美国核管制委员会(Nuclear Regulatory Commission, NRC)在2011年发布了ANSI/ANS-5.4-2011标准，该标准详细介绍了NRC推荐的计算裂变产物释放产生比的方法，且在原有的标准基础上进行了最优化改进和参数修正，提高了计算的准确性。为对压水堆一回路源项进行准确分析，确定较为准确的计算裂变产物释放产生比的方法，本文对NRC发布的ANSI/ANS-5.4-2011标准和原来的ANSI/ANS-5.4-1982标准以及法国METEOR1.5程序方法进行了研究分析和对比。

1 扩散与释放模型的建立与求解

由于UO2核芯颗粒可近似为球形，因此裂变产物在其中的扩散可用球坐标下的扩散方程描述[3]。

主裂变产物在UO2颗粒中的扩散遵循菲克扩散定律[4]：

式中，C为燃料中的核素浓度，cm−3；t为时间，s；B代表核素产生率，cm−3·s−1；λ代表核素衰变常数，s−1；r是燃料球的半径，cm；D为核素的扩散系数，cm2·s−1。

当反应堆功率基本稳定时可以将芯块晶粒中裂变气体产物浓度视为稳定，有：

于是基本方程可简化为：

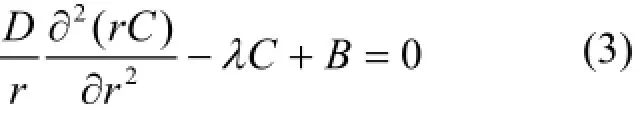
令y=rC，则有：

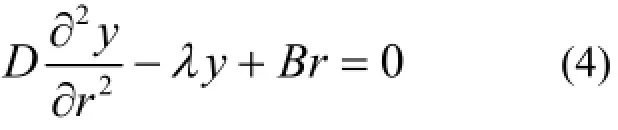
解以上常微分方程可得：

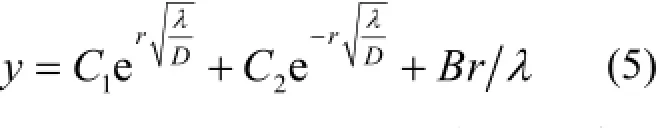
当r=0时，C1+C2=0，即C2=−C1；当r=a时，C=0，则有：

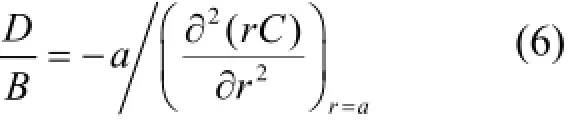
由式(5)、(6)可得，燃料晶粒的裂变产物释放产生比：

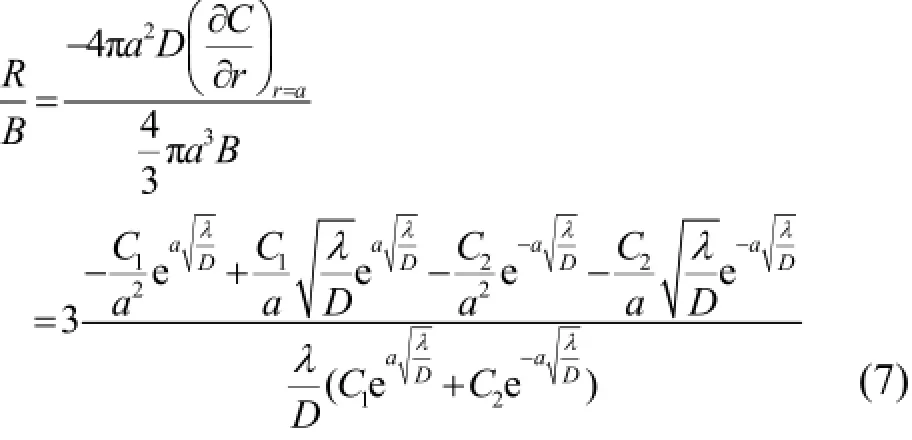
令μ=λa2/D（无量纲化），则释放产生比为：

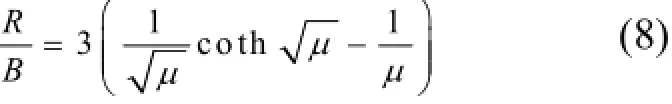
对于球形晶粒半径a有：a=3V/S（V为晶粒体积，S为表面积），则式(8)可变形为：

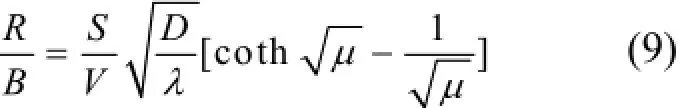
对于尺寸极小的晶粒来说其μ值极小，因此式(9)可近似为：

式(10)是式(9)相对保守的近似，其误差小于2%。

2 裂变产物释放产生比计算方法

2.1 ANSI/ANS-5.4标准

美国NRC发布了用于计算反应堆功率稳定情况下气体裂变产物释放产生比的ANSI/ANS-5.4标准，其最新版本为ANSI/ANS-5.4-2011。ANSI/ANS-5.4-2011在旧的较保守的ANSI/ANS-5.4-1982基础上进行了估算方法的优化、参数的修正以及适用范围的扩充（ANSI/ANS-5.4-1982标准仅适用于燃耗在1 GWd·tU−1以下的UO2燃料棒的计算[5]）。

在ANSI/ANS-5.4-2011中引入了先驱核因子的无量纲修正因子α，即式(10)被修正为：

ANSI/ANS-5.4-2011中的扩散系数D是根据Turnbull等[6]在1982年提出的关系式修正而来，即：

式中，Di为扩散系数，m2·s−1；Ti为燃料温度；F代表裂变率。第一项为高温时芯块的固有扩散系数；第二项为因辐照引发铀的空位机制而增加的扩散系数；第三项为因辐照直接引发的扩散系数。

ANSI/ANS-5.4-2011还用了一个简单的经验关系式—Vitanza临界准则来考虑晶间的气泡联合效应。即燃耗Bu≤18.2 MWd·kg·U−1时，晶间气泡开始联合的温度为：

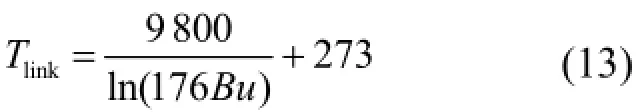
当燃耗Bu＞18.2 MWd·kgU−1时，晶间气泡开始联合的温度：

式中，Tlink是在给定的计算节点处的温度，K。由以上关系确定的燃料节点i处的半衰期小于6 h裂变产物释放产生比为：

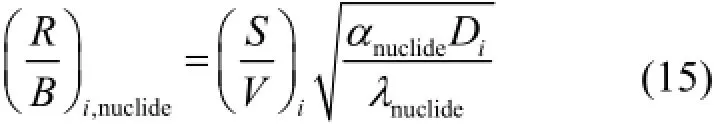
半衰期大于6 h但小于60 d的裂变产物释放产生比为：

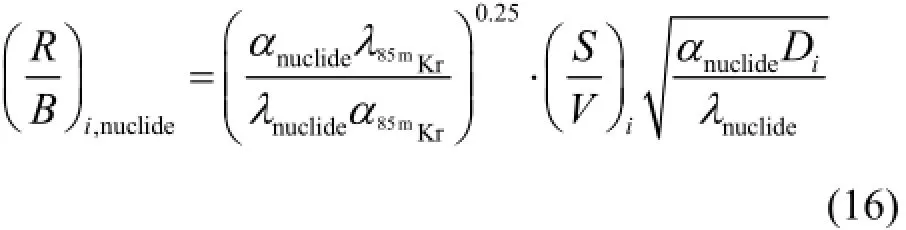
式中，当Ti≤Tlink时，S/V=120 cm−1，当Ti＞Tlink时，S/V=650 cm−1，Ti为i节点处的燃料温度。

2.2 法国计算方法

法国METEOR 1.5程序中，其裂变气体扩散系数由热项、无热项以及联合项三项构成[7]。

热项：

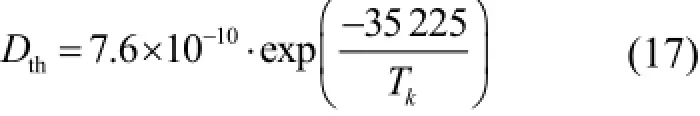
无热项：

联合项：

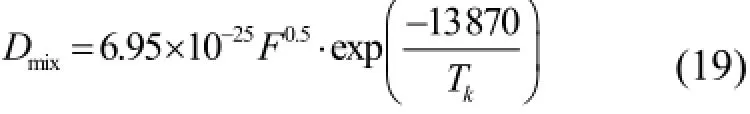
式中，F为裂变密度，m−3·s−1；Tk为燃料的局部温度，K。

3 整根燃料棒释放产生比计算模型

利用以上方法进行计算时先将燃料棒的径向和轴向进行网格划分使燃料棒划分为若干个环状单元，计算时假定每个环状单元内的温度以及燃耗相等，据此分别计算出每个环状单元的释放产生比，然后根据每个单元处的功率水平、体积以及释放产生比进行加权平均即可得到整个燃料棒的释放产生比。对于径向节点为k、轴向节点为j的燃料棒，其释放产生比可表示为：

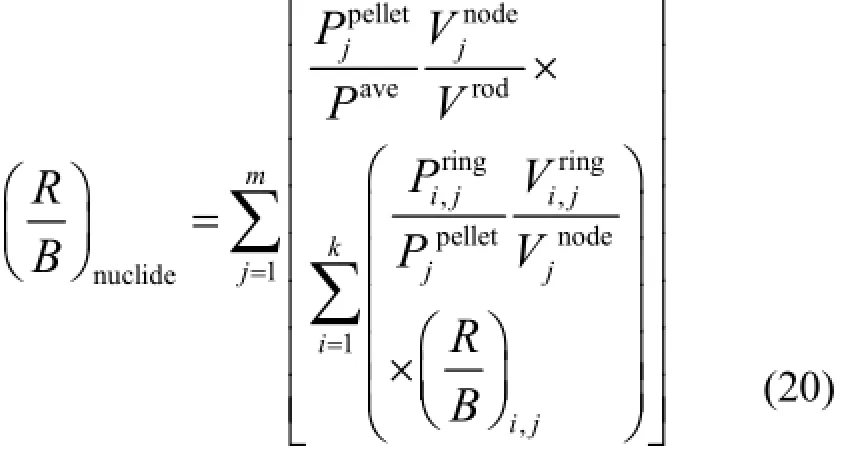
式中，P是功率，kW·ft−1，ave=棒的平均值，pellet=轴向平均值，ring=径向环；V为体积，cm3，rod=棒的总体积，node=轴向节点体积，ring=径向环体积。燃料棒的网格划分如图1所示，整根燃料棒的释放产生比的MATLAB计算流程如图2所示。

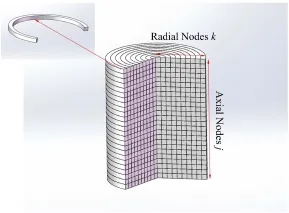
图1 燃料棒网格划分Fig.1 Grid of the fuel rod.

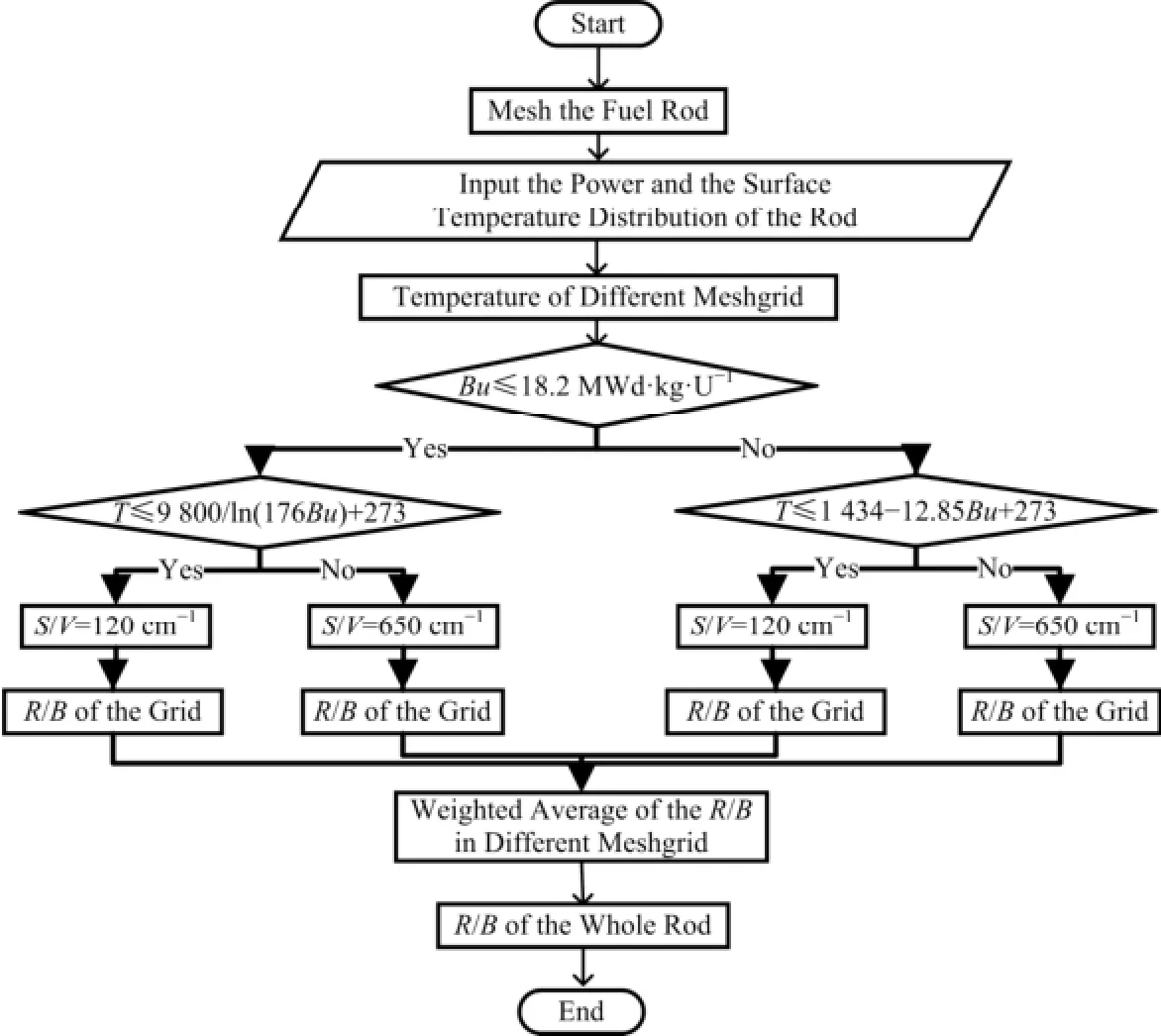
图2 计算燃料棒的释放产生比流程Fig.2 Calculation process of the release to birth ratio .

4 结果分析

4.1 不同功率水平下的释放产生比

研究UO2燃料棒功率水平对于燃料棒裂变产物释放产生比的影响，以ANSI/ANS-5.4-2011中数据匹配较好的核素85mKr (4.48 h)和较为常见的半衰期较长的核素131I (8.04 d)为研究对象，分别利用ANSI/ANS-5.4-2011标准、ANSI/ANS-5.4-1982标准以及法国METEOR 1.5程序的方法计算百万千瓦级压水堆核电站的UO2燃料棒从10%功率到满功率时85mKr以及131I的释放产生比，得到的结果如图3。

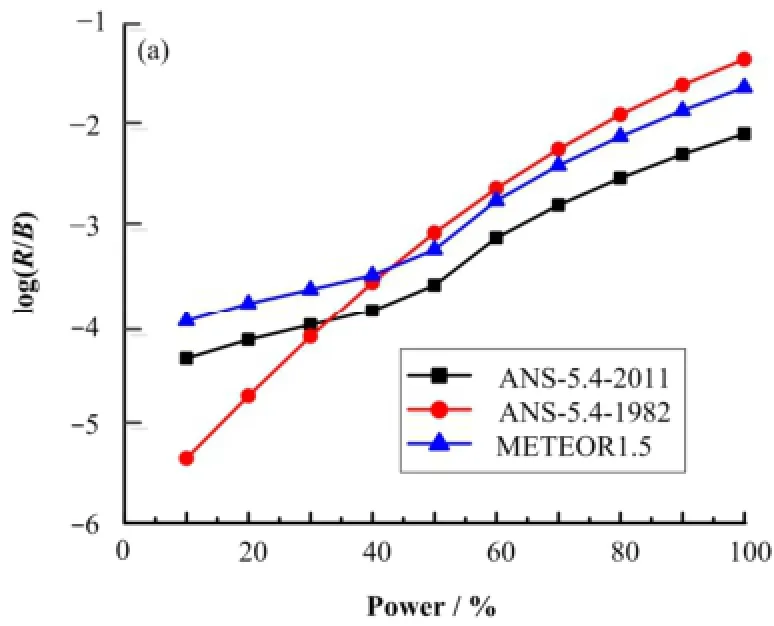
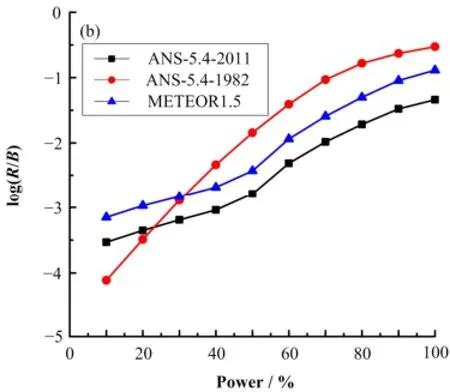
图3 85mKr (a)和131I (b)在不同功率水平下的释放产生比Fig.3 Release to birth ratio of 85mKr (a) and 131I (b) at different power.

将几种方法的计算结果进行对比，结果表明，当燃料棒功率水平增加时其裂变产物的释放产生比也增大，在不同的功率水平下法国METEOR 1.5程序的计算方法相较于ANSI/ANS-5.4-2011标准更保守，功率水平较高时ANSI/ANS-5.4-1982最保守。

4.2 不同燃耗下的释放产生比

为研究燃耗对于裂变产物释放产生比的影响，分别利用ANSI/ANS-5.4-2011标准、ANSI/ANS-5.4-1982标准以及法国METEOR 1.5程序的方法计算UO2燃料棒燃耗从1 GWd·tU−1到60 GWd·tU−1时85mKr以及131I的释放产生比，并将不同燃耗下计算得到的131I的释放产生比结果与Halden实验[8]所得数据进行对比，最终得到的结果如图4所示。

结果表明，ANSI/ANS-5.4-2011标准的计算结果与实验结果符合最好，在几种方法中能最准确地计算出裂变产物的释放产生比。当UO2燃料棒燃耗增加时其裂变产物的释放产生比会增大，在不同的燃耗下法国METEOR 1.5程序的计算方法相较于ANSI/ANS-5.4-2011标准更保守，在ANSI/ANS-5.4-1982标准适用燃耗范围内ANSI/ANS-5.4-1982标准最保守。

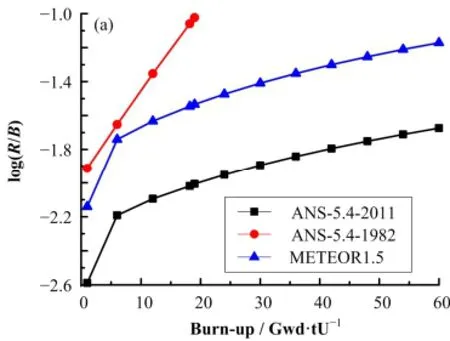
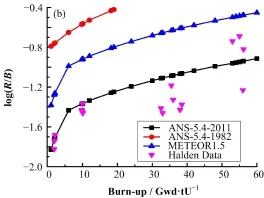
图4 不同燃耗下85mKr (a)和131I (b)释放产生比Fig.4 Release to birth ratio of 85mKr (a) and 131I (b) at different burn-up.

5 结语

根据以上计算结果对比分析得出如下结论：

(1) 不同功率水平下裂变产物释放产生比的计算表明，当UO2燃料棒燃耗一定时其裂变产物的释放产生比会随着功率水平而增大。

(2) 不同燃耗下裂变产物释放产生比的计算表明，当UO2燃料棒处于满功率运行状态时，其裂变产物的释放产生比会随着其燃耗而增大。

(3) 几种方法计算结果与实验数据的对比表明，ANSI/ANS-5.4-2011标准的计算结果与实验结果符合最好，在几种方法里能最准确地计算出裂变产物的释放产生比。METEOR 1.5程序的计算方法相对于ANSI/ANS-5.4-2011标准更保守，而ANSI/ANS-5.4-1982标准在几种方法中最保守（除低功率水平外）。

综上所述，ANSI/ANS-5.4-2011在原来方法的基础上进行了优化修正，不但对适用范围进行了拓展，其计算结果相对于原有标准也更准确，能较好地适用于压水堆核电站裂变产物释放份额的计算。

1 Brillant G, Marchetto C, Plumecocq W. Fission product release from nuclear fuel I: physical modelling in the ASTEC code[J]. Annals of Nuclear Energy, 2013, 61: 88–95

2 伍怀龙, 郝樊华, 唐元明. 反应堆中气体裂变产物释放问题的研究[J]. 核技术, 2007, 30(7): 633–636 WU Huailong, HAO Fanhua, TANG Yuanming. Investigation of fission gases release in nuclear reactors[J]. Nuclear Techniques, 2007, 30(7): 633–636

3 房超. 半衰期为数天的惰性气体和卤素裂变产物在UO2颗粒中的扩散与释放[J]. 原子能科学技术, 2013, 47(1): 109–113 FANG Chao. Diffusion and release of noble gas and halogen fission products with several days half-life in UO2particle[J]. Atomic Energy Science and Technology, 2013, 47(1): 109–113

4 Verfondern K, Nabielek H, Moormann R, et al. Fuel performance and fission product behavior in gas cooled reactors[R]. IAEA-TECDOC-978, Vienna: IAEA, 1997

5 ANSI/ANS-5.4-1982, Method for calculating the fractional release of volatile fission products from oxide fuel[S]. U. S. NRC, 1982

6 ANSI/ANS-5.4-2011, Method for calculating the fractional release of volatile fission products from oxide fuel[S]. U. S. NRC, 2011

7 何晓军, 陈彭. 燃料元件行为分析程序METEOR l.5的校核[J]. 核动力工程, 2007, 28(2): 12–15 HE Xiaojun, CHEN Peng. Validation of fuel behavior analysis code METEOR 1.5[J]. Nuclear Power Engineering, 2007, 28(2): 12–15

8 Turnbull J A, Beyer C E. Background and derivation of ANS-5.4 standard fission product release model[M]. U. S. NRC, 2010

CLC TL99

Methods for calculating the release to birth ratio of volatile fission products

XU Rui1DONG Bing1FU Yaru2MEI Qiliang2WANG Dezhong1
1(Shanghai Jiao Tong University, Shanghai 200240, China) 2(Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China)

Background: A large quantity of fission products would be produced when the nuclear reactor runs. These fission products would be released to the pellet-rod gap and then to the primary circuit while the fuel rod is broken. The fission products in the primary circuit become the main source term of the reactor. Purpose: This study aims to analysis the source term accurately by calculating the release to birth ratio (RBR) of volatile fission products precisely. Methods: After researching American NRC ANSI/ANS-5.4 methods and French methods for calculating the RBR of volatile fission products, we calculated the RBR of volatile fission products of a fuel rod at different power and different burn-up by these methods, and made some comparison and analysis of these results. Results: Computation results showed that the RBR of volatile fission products would increase with the power and burn-up of the fuel rod. Compared with the ANSI/ANS-5.4-2011, the French method is more conservative whilst the ANSI/ANS-5.4-1982 is the most conservative among these methods. Conclusion: ANSI/ANS-5.4-2011 is the best method among these three methods and it can be used to calculate the release to birth ratio of volatile fission products with good results.

Fuel rod, Fission products, Release to birth ratio, ANSI/ANS-5.4, METEOR1.5

TL99

10.11889/j.0253-3219.2015.hjs.38.040605

No.11175118)、上海市教育委员会科研创新项目(No.12ZZ022)资助

许锐，男，1990年出生，2012年毕业于上海交通大学，现为硕士研究生

王德忠，E-mail: dzwang@sjtu.edu.cn

2014-12-26，

2015-02-05