一维四元嵌构式声子晶体低频禁带特性研究

邱学云（文山学院信息科学学院，云南 文山 663099）

声子晶体具有的声波禁带特性可以被应用于振动控制、隔音、声滤波器、波导、超声换能器等。因此，对声子晶体的研究成为电子晶体和光子晶体之后的又一种人工编织的周期性复合材料。理论设计出能在一定频率范围内抑制振动传播的声子晶体结构，对实现结构的声功能特性有着重要的意义［1］。根据声子晶体的周期排列形式，一般分为一维、二维和三维结构。其中一维声子晶体构造最为简单，所以在实际应用中的可能性最大。对一维声子晶体的研究已经在理论计算、模拟仿真和实验研究3个方面取得阶段性成果［2－11］。但对于层状四元声子晶体的带隙分析和研究目前未见报道。为此，笔者根据声子晶体理论，基于多层周期性层状结构在减振隔音方面的应用可能，构造了一个层状四元复式声子晶体模型，采用集中质量法计算该结构的禁带特性，分析其禁带变化规律，这为周期性减振隔音复合板材的设计提供了一种新思路。

1 理论模型

实际工程中的有限层状结构与理想的一维层状声子晶体结构类似，都由不同的多层平板材料沿着垂直于平面材料的方向上具有周期性。因此，笔者构造了一个层状四元复式声子晶体模型。一维层状声子晶体的振动模式以沿周期方向的弹性波的纵波激发为主，因此，笔者选择的层状四元复式声子晶体仅考虑纵波带隙特性。

图1是一维四元声子晶体模型。当仅取周期方向为垂直于材料层面的X方向时，该结构与一维杆状声子晶体模型相同。设该模型由A、B、C、D这4种非金属材料沿X方向交替排列构成，取1个周期中A、B、C、D这4种材料的长度分别为d1、d2、d3、d4，即1个晶格常数a＝d1＋d2＋d3＋d4。

图1 一维四元嵌构式声子晶体模型

选取组成该一维四元嵌构式声子晶体的4种材料：A为石灰岩，B为coca31－20－50，C为丁腈橡胶，D为coca31－20－30（4种材料的有关物理参数如表1所示），这是在传统一维二组元石灰岩／丁腈橡胶声子晶体之间分别嵌入2种硅酮橡胶coca31－20－50和coca31－20－30，建构一个层状非金属四组元声子晶体结构。根据固体物理学中的能带理论，若层状周期结构的长度与宽度远大于层状周期结构的晶格常数，则该结构可视为一维声子晶体结构。同时，入射波只考虑沿OX方向传播的平面波为纵波，此时，层状声子晶体的振动情况与杆状声子晶体的振动情况相同，与固体物理学中周期性弹簧振子结构类似。可以采用集中质量法的思想，假设组成该声子晶体的材料都是理想弹性均匀介质，可将其均匀地离散化。已有部分文献基于集中质量法对一维声子晶体的能带结构进行计算［2～7］，研究表明集中质量法能更加直观地描述声子晶体内部作用机理，方法正确可靠。

图2是采用集中质量法计算得到的一维AB型（石灰岩／丁腈橡胶）层状声子晶体能带结构图，该声子晶体晶格常数 为0.04m，计算中每个原胞简化为自由度数为320的弹簧振子结构，选取石灰岩／丁腈橡胶的厚度相同，自由度数都为160。基于Matlab编程计算画图就能得到图2所示结果，图2中阴影部分从下到上分别为该声子晶体的第1、2带隙，可见起止频率都很大。图3是与一维AB型（石灰岩／丁腈橡胶）层状声子晶体晶格常数、总自由度数和计算方法都相同，计算得到的一维ACBD型（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）层状四元声子晶体能带结构图，从图3可以看出，该四元嵌构式声子晶体第1、2带隙的起止频率都很小。显然在二元AB型层状结构中嵌入密度和杨氏模量都很小的2种硅酮橡胶能够极大地改变结构的能带分布情况。

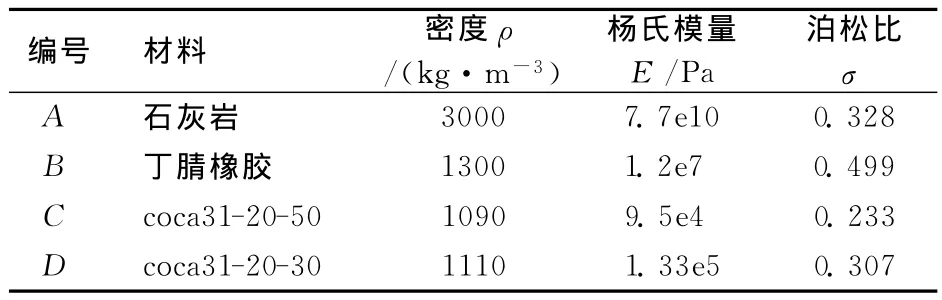
表1 4种材料的物理参数

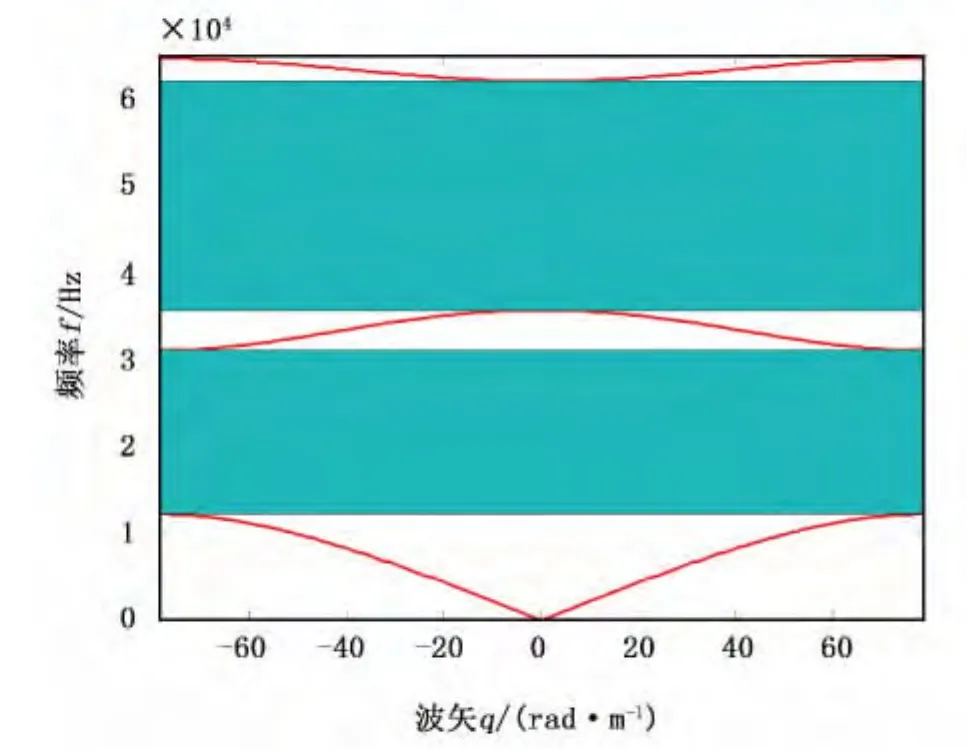
图2 一维AB型声子晶体能带结构图

图3 一维ACBD型声子晶体能带结构图

2 组合类型变化对带隙特性的影响

对二元AB型与ACBD型层状结构，分别取相同的晶格常数为0.04m，组份比为1，即各种材料的厚度相同，分别计算第1、2带隙的频率分布情况，结果见表2。

由表2可知，二元AB型声子晶体可以看成四元AABB型声子晶体，当把其中的一半A材料和B材料分别替换成C材料和D材料时，就能组合成四元嵌构式声子晶体。从表2的计算结果可以看出二元AB型声子晶体第1带隙的起止始频率分别比四元ACBD型声子晶体的高92倍和160倍。显然，嵌构式四元声子晶体能有效改变二元结构的带隙分布，且从四元ACBD型声子晶体的带隙情况可以看出该组合结构能很好地控制低频声波。

表2 2种结构不同组合类型的带隙情况

另外，对于四元ACBD型声子晶体，当C材料和D材料的嵌构位置变化时，第1、2带隙的起止频率又会发生变化。如选择ACBD型（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）与ACDB型（石灰岩／coca31－20－50／coca31－20－30／丁腈橡胶）结构进行比较，发现ACDB型组合的第1带隙起始频率比ACBD型组合的第1带隙起始频率低，差值为15.1945Hz，且ACDB型组合的第1带隙比ACBD型组合的第1带隙的带宽增大了108.678Hz。同时，也发现ACDB型组合的第2带隙起始频率比ACBD型组合的第2带隙起始频率增高了82.9293Hz，带隙宽度减小了61.1298Hz。ABCD型与ACDB型排列情况类似，都是密度和杨氏模量都较小的C／D材料集中嵌构在A／B或B／A材料中，所以两者的带隙分部差别很小。显然，嵌构式四元声子晶体中，密度和杨氏模量都较小的C／D材料集中排列，能更好地获得第1带隙低频宽带的要求，更有利于实现低频声波的控制。

3 晶格常数对带隙的影响

对于4种材料复合成的一维四元声子晶体，选择ACBD型（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）为对象，固定各材料的密度、弹性模量，仅改变材料的晶格常数来计算其带隙变化的情况。图4给出了一维四元ACBD型（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）声子晶体带隙与晶格常数的关系。计算中设定该系列声子晶体中各层材料的厚度相同，且每种材料自由度数都取80，取晶格常数由0.02m增大到0.12m。由图4可以看出，随着晶格常数a的增大，该一维四元声子晶体的第1、2带隙的起止频率都逐渐减小，并且2个带隙的带宽也逐渐减小。减小的程度随着晶格常数的增大第1带隙减小缓慢，第2带隙减小迅速，但都同时向低频率区靠近。所以可通过调节声子晶体晶格常数的大小来获得所需的带隙。

图4 晶格常数与一维ACBD型声子晶体带隙的关系

图5 材料厚度与一维ACBD型声子晶体带隙的关系

4 组分比变化对带隙特性的影响

对于一维四元ACBD型（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）声子晶体，当保持该声子晶体的晶格常数不变，保持各材料的密度、弹性模量不变，仅改变材料的组分比，即改变组合材料的厚度时，也可以改变该声子晶体的带隙分布。图5是选取组成该类型声子晶体材料的密度、弹性模量不变，晶格常数固定为0.32m，同时增大A、B、C这3种材料的厚底，减小D材料的厚度，即A、B、C这3种材料的组分比同时等比例增大，D材料的组分比减小，通过计算得到的一维ACBD型声子晶体带隙分布情况。

从图5可以看出，随着A、B、C这3种材料的厚度由6mm增大到10mm，该系列声子晶体第1带隙起始频率逐步减小、截止频率逐步增大，第1带隙带宽逐步展宽。当d取10mm时，第1带隙带宽最大为239.4Hz。同时，第2带隙起始频率逐步增大、截止频率先增大后减小，第2带隙带宽先增大后减小。当4种材料厚度同为8mm，即组分比为1时，第2带隙带宽最大为352.1Hz。显然，组分比变化对带隙的调控也很明显，必要时，也可以通过调节声子晶体组分比即组合材料的厚度来获得所需的带隙。

5 结论

当把一维二元AB型声子晶体看成四元AABB型声子晶体时，将其中一半A材料和一半B材料分别替换成C材料和D材料时，就能组合成四元嵌构式声子晶体。选取4种非金属材料石灰岩、丁腈橡胶、coca31－20－50、coca31－20－30构成一个代表性结构模型进行系列计算，结果表明：

1）晶格常数都为0.04m的一维二元（石灰岩／丁腈橡胶）层状声子晶体第1带隙的起始频率为12143Hz，第2带隙的截止频率为62086Hz，2个频率都很高；一维四元（石灰岩／coca31－20－50／丁腈橡胶／coca31－20－30）嵌构式层状声子晶体的第1带隙起始频率为132.1222Hz，第2带隙截止频率为534.6435Hz，2个频率都很低，这一禁带特性能够实现低频声波的控制。

2）在4种非金属材料石灰岩、coca31－20－50、丁腈橡胶、coca31－20－30的不同组合中，密度和杨氏模量都较小的2种硅酮橡胶材料coca31－20－50、coca31－20－30集中排列时，一维四元ACDB层状声子晶体的第1带隙更容易实现低频宽带的要求。

3）随着晶格常数的增大，一维四元嵌构式声子晶体第1、2带隙的起止频率和带宽都会减小，第1带隙减小缓慢，第2带隙减小迅速，但都向低频率区靠近。

4）对于一维四元嵌构式声子晶体，组分比变化对带隙的调控也很明显。必要时，也可以通过调节声子晶体组分比即组合材料的厚度来获得所需的禁带带隙。

［1］John S.Strong localization of photons in certain disordered dielectric［J］.Phys Rev Lett，1987，58（23）：2486.

［2］Sigalas M M，Soukoulis C M.Elastic－wave propagation through disordered and／or absorptive layered systems［J］.Phys Rev B，1995，51（5）：2780.

［3］吴福根，刘有延.二维周期性复合介质中声波带隙结构及其缺陷态［J］.物理学报，2002，51（7）：1434.

［4］Jensen J.Phononic band gaps and vibrations in one－and two－dimensional massspring Structures［J］.J Sound Vib，2003，266：1053～1078.

［5］温激鸿，王刚，刘耀宗，等.基于集中质量法的一维声子晶体弹性波带隙计算［J］.物理学报，2004，53（10）：3384.

［6］胡家光，张晋，张茜，等.一维花岗岩／丁腈橡胶声子晶体的带隙及其应用［J］.云南大学学报：自然科学版，2006（6）：504～508.

［7］Wang G，Wen J H，Liu Y Z，et al.Lumped－mass method for the study of band structure in two－dimensional phononic crystals［J］.Phys Rev B，2004，69：184302.

［8］Wang G，Wen J H，Wen X S：Quasi－one－dimensional phononic crystals studied using the improved lumped－mass method：Appli－cation to locallyresonant beams with flexural wave band gap［J］.Phys Rev B，2005，71：104302.

［9］Wang G，Wen X S，Wen J H，et al.Two－Dimensional Locally Resonant Phononic Crystals with Binary Structures［J］.Phy Rev Lett，2004，93（15）：154302.

［10］温激鸿，王刚，郁殿龙，等.声子晶体振动带隙及减振特性研究［J］.中国科学E辑，2007，37（9）：1126～1139.

［11］Liang B，Yuan B，Cheng J C.Acoustic diode：Rectification of acoustic energy flux in one－dimensional systems［J］.Phys Rev Lett，2009，103：104301.