PDC钻头扭转冲击破岩机理及试验分析

李思琪，闫铁，李玮

（东北石油大学石油工程学院，黑龙江 大庆163318）

毕福庆

（中石油大庆油田分公司第五采油厂试验大队，黑龙江 大庆163513）

PDC钻头作为主要的破岩工具之一，近几年随着深部地层勘探开发比例的增加，其应用比例也随之增加［1，2］。但由于PDC钻头破岩时产生黏滑振动，引发PDC钻头过早失效，因此大大降低了机械钻速和使用寿命，这是PDC钻头亟需解决的问题之一［3］。

目前有关PDC钻头破岩机理的研究较多。Chen Yinghua［4］通过试验研究了单个切削齿与岩石的相互作用。Kaitkay等［5］用单个PDC片在不同静水压力下对岩石进行了切削试验，研究发现切削力会随着切削角度和静水压力的变化而变化。王镇全等［6］选用砂岩、页岩为代表岩性，优化了切削齿的切削角度。谌湛［7］建立了PDC钻头力学模型，通过试验手段对PDC钻头的受力问题进行了深入研究。Detournay等［8］对PDC钻头钻进时各项钻进参数之间的关系建立了理论模型，并通过试验研究对钻进时的摩擦特性进行了研究。

现有的研究中，主要通过扭转冲击器［9］和优化钻井参数［10］来解决PDC钻头黏滑效应，其根本均是通过施加稳定的扭矩来保证PDC钻头高效工作。但通过以上调研可知，对扭转条件下PDC钻头的破岩机理鲜有研究。因此，笔者通过建立在扭转冲击载荷作用下PDC钻头单刀翼、多刀翼与岩石相互作用模型，并通过室内试验进行理论验证，研究PDC钻头扭转冲击破岩机理，为PDC钻头的高效破岩奠定理论基础。

1 扭转冲击破岩机理

PDC钻头在扭转冲击载荷作用下破碎岩石，钻头与岩石作用面处的扭矩T（t）与钻压W（t）同时作用于切削齿。钻头的运动方程由钻压、扭矩、钻速及转速等因素确定，其在周向及轴向的运动方程分别为：

图1 单刀翼与岩石作用的力学模型

式中：I为钻头的转动惯量，kg·m2；φ（t）为在时间t时钻头的角度，rad；C为钻头的扭转刚度，N·m2；Ω为钻头的角速度，rad／s；M为钻头的质量，kg；U（t）为在时间t时钻头的垂向位置，m；T（t）为钻头的瞬时扭矩，N·m；W0为钻柱作用于钻头上的瞬时钻压，kN；W （t） 为在时间t时钻柱作用于钻头上的钻压，kN。

岩石破碎过程包括切削过程和摩擦过程，在这两个过程中岩石同时受到扭矩T（t）和钻压W（t）的作用。则有：

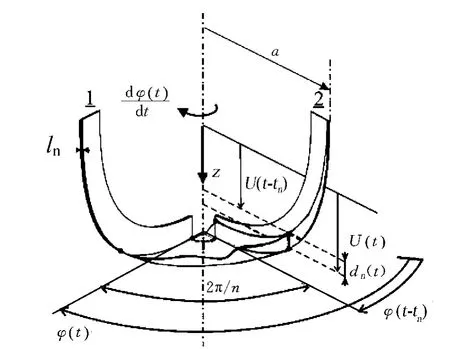
图2 多刀翼与岩石作用的力学模型

式中：Tc（t）、Tf（t）分别为岩石切削、摩擦过程时的扭矩，N·m；Wc（t）、Wf（t）分别为岩石切削、摩擦过程时的钻压，kN。

建立PDC钻头单刀翼与岩石作用的力学模型，如图1所示，刀翼同时受剪切力Fc和摩擦力Ff作用，其中剪切力和摩擦力又分为垂向分力和水平分力。由几何关系可得：

式中：Fcs为水平方向剪切力，N；Fcn为垂直方向剪切力，N；Ffs为水平方向摩擦力，N；Ffn为垂直方向摩擦力，N；ε为岩石破碎比功，J／m3；ω是刀翼的宽度，m；d为刀翼累积垂直切削深度，m；ζ为切削力方向描述参数，1；μ为摩擦因数，1；σ为接触面上最大的接触力，Pa；l为刀翼摩擦面沿径向长度，m。

破岩时PDC钻头多个刀翼同时工作，建立相邻刀翼间的运动受力模型，如图2所示，每个刀翼间的夹角均为2π／n。综合所有刀翼的作用，在切削过程中，对岩石起作用的钻压和扭矩为：

式中：dn（t）为随时间变化的切削垂深，m；n为刀翼个数，1；a为刀翼边缘距钻头中心轴线的距离，m。在摩擦过程中，对岩石起作用的钻压和扭矩为：

式中：γ为钻头几何形状参数（＞1），1；ln为刀翼的厚度，m。

由于有恒定的扭矩作用于PDC钻头，使得PDC钻头可以保持稳定的垂向切削与水平切削，从而解决了PDC钻头钻进时的黏滑现象，大大提高了机械钻速。

2 试验装置及测试系统

试验装置为东北石油大学高效钻井破岩技术研究室自主研发的 “动静载荷机械破岩实验系统”（如图3）。

实验系统主要由主机架、扭转冲击系统、轴载系统、围压系统以及数据采集控制系统等部分构成。其功能主要是研究高频扭转冲击载荷作用下钻头的破岩性能以及岩石抵抗钻头等破岩工具的能力。设备的扭转冲击频率为0～3000Hz，扭转冲击力为0～1500N·m，轴向静压载荷为0～10kN，转速为0～500r／min，岩石试样的长×宽×高范围为（100～300）mm×（100～300）mm×（100～300）mm。

图3 动静载荷机械破岩实验系统示意图

3 试验结果及分析

3.1 试验设计

室内试验使用的PDC钻头的直径为75mm，切削齿直径分别为13.5mm，后倾角为15°，如图4所示，具体试验参数如表1所示。分别对红砂岩、黄砂岩进行有无扭转冲击的对比试验，如图5、6所示。试验以自来水为钻井液，携带岩屑和冷却钻头，记录钻时、扭矩、钻压、转速、位移和钻进速度等数据。

表1 试验参数表

图4 直径为75mm的PDC微钻头

图5 黄砂岩钻进试验

图6 红砂岩钻进试验

试验主要用来分析在扭转冲击条件下，扭矩、钻压、转速等参数对机械钻速的影响。

3.2 试验结果分析

在转速为200r／min、钻压为9kN、扭矩为25N·m的条件下，对红砂岩进行有无扭转冲击载荷的钻进试验，测得试验数据曲线如图7所示。

图7表明，在相同的钻进参数条件下，钻进相同深度的红砂岩时，施加扭转冲击载荷的试验所需时间明显低于只施加轴向静压载荷的时间，节约钻进时间约36.6%。说明扭转冲击作用大大提高了PDC钻头的机械钻速，这是由于恒定扭矩的作用消除了PDC钻头的黏滑效应。

在钻压为15kN、扭矩为25N·m的条件下，改变不同转速，对红砂岩进行有无扭转冲击载荷的钻进试验，测得试验数据曲线如图8所示。

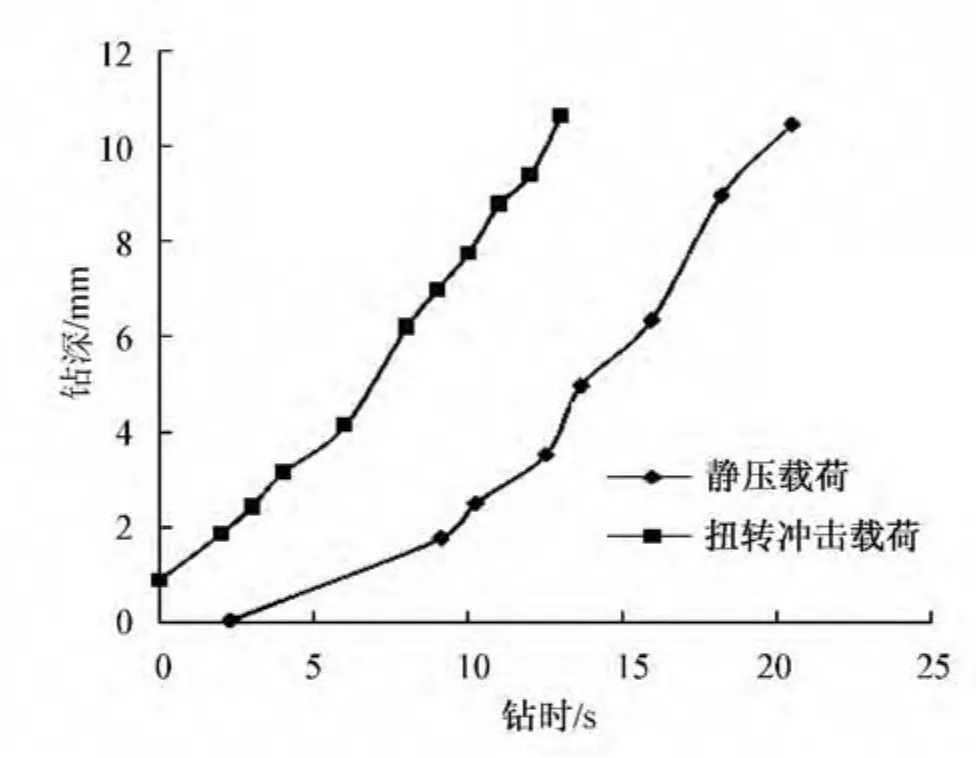
图7 动、静载荷下的钻时与钻深关系曲线

图8 动、静载荷下钻速与转速关系曲线

图8为钻速与转速之间的关系曲线图，其中转速分别为100、150、200r／min。由图8可以看出，随着转速的增加，PDC钻头的钻速随之增加，并且有扭转冲击载荷下的PDC钻头钻速均高于同等条件下静压载荷下PDC钻头的钻速，平均增长幅度为116.8%。

在转速为200r／min、扭矩为25N·m的条件下，改变不同钻压，对黄砂岩进行有无扭转冲击载荷的钻进试验，测得试验数据曲线如图9所示。

图9为钻速与比钻压之间的关系曲线图。此处比钻压是指钻压与PDC钻头直径的比值，大小分别为0.12、0.2、0.28。从图9中可以看出PDC钻头的钻速随着比钻压的增大先增大后减小，说明钻压与PDC钻头的尺寸存在一个合理的匹配范围。对于黄砂岩，钻头直径为75mm的PDC钻头的最佳比钻压为0.16～0.24kN／mm。另外由曲线对比可知，相同条件下施加扭转冲击载荷的PDC钻头钻速高于静压载荷条件下PDC钻头钻速，最高达到静压载荷条件下PDC钻头钻速的152.3%。

图9 动、静载荷下钻速与比钻压关系曲线

4 结论

1）分别建立了PDC钻头单刀翼、多刀翼与岩石相互作用模型，分析了PDC钻头扭转冲击破岩机理。模型分析表明，扭矩和钻压同时作用于PDC钻头破岩过程中的切削和摩擦过程，恒定的扭矩作用解决了PDC钻头钻进时的黏滑现象，大大提高了机械钻速。

2）红砂岩对比试验可知：在扭转冲击载荷作用下，钻进相同深度红砂岩，可节约钻进时间36.6%；在不同转速条件下，钻速平均增长幅度为116.8%。

3）黄砂岩对比试验可知：在扭转冲击载荷作用下，PDC钻头钻速最高达到静压载荷条件下PDC钻头钻速的152.3%；钻头直径为75mm的PDC钻头的最佳比钻压为0.16～0.24kN／mm。

［1］张克勤，张金成，戴巍.西部深井超深井钻井技术 ［J］.钻采工艺，2010，33（1）：36～39.

［2］张克勤.元坝地区钻井难题分析与技术对策探讨论 ［J］.石油钻探技术，2010，38（3）；27～31.

［3］Jens R，Dmitriy D.Development of an innovative model－based stick／slip control system ［J］.SPE／IADC139996，2011.

［4］Chen Yinghua.Experimental study of rock－breaking with an offset single cone bit ［J］.Pet Sci，2008，（5）：179～182.

［5］Kaitkay P，Lei S.Experimental study of rock cutting under external hydrostatic pressure ［J］.Journal of Materials Processing Technology，2005，159：206～213.

［6］王镇全，周悦辉.PDC钻头切削齿切削角度对破岩效果影响规律的研究 ［J］.煤矿机械，2009，30（8）：49～51.

［7］谌湛.PDC钻头力学模型实验研究 ［D］.北京：中国石油大学，2011.

［8］Detournay E，Richard T，Shepherd M.Drilling response of drag bits：Theory and experiment ［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2008，45：1347～1360.

［9］祝效华，汤历平，吴华，等.扭转冲击钻具设计与室内试验 ［J］.石油机械，2011，39（5）：27～29.

［10］Xianping Wu，Luis Paez，Uyen Partin，et al.Decoupling stick－slip and whirl to achieve breakthrough in drilling performance ［J］.SPE／IADC128767，2010.