CASIO计算器全路线程序计算
2015-12-01聂有军聂有杰
聂有军 聂有杰
(内蒙古阿拉善盟S218线巴苏一级公路建管办,内蒙古自治区阿拉善盟 750306)
CASIO计算器全路线程序计算
聂有军 聂有杰
(内蒙古阿拉善盟S218线巴苏一级公路建管办,内蒙古自治区阿拉善盟 750306)
公路工程、市政道路工程、桥梁工程的施工过程中,设计坐标、设计标高现场计算是频率较高的一项工作。现采用CASIO-5800做为编程工具,编写了全路线坐标计算程序、全路线标高计算程序、全路线坐标反算桩号程序三组全路线计算程序。本程序主要适用于CASIO-4800、CASIO-4850、CASIO-4850计算器。
CASIO-4800计算器 CASIO-4850计算器 CASIO-4850计算器
1 前言
为了兼顾在CASIO-4800/CASIO-4850计算器上应用,路线元素输入中,采用即时校核改错输入方式,方便输入与校对改错。程序编写过程中尽可能使程序短小精简,便于手工输入程序与节约内存。全路线参数一次输入计算器存储容量不够用时,可以输入部分路线参数分段使用。CASIO-4800/CASIO-4850计算器不能使用变量定义扩充变量存储器。自定义存储器个数需要手工设置,自定义存储器个数设置为:(Z[6]+1)×6+Z[5]×3。Z[6]为平曲线个数;Z[5]为竖曲线个数(包括起点与终点)。CASIO-5800计算器,计算器程序根据输入的曲线个数自动设置。
2 程序特点
(1)以交点桩号、坐标为基础数据,避免了路线全系统错误的发生。
(2)路线断链自动处理。按设计图纸修改断链子程序序中的断链桩号。
(3)统一设置分配变量、参数存储器。三组程序根据需要任意切换调用,不影响各自的基础参数。
(4)只输入最基本的必需参数,如竖曲线的凹凸判别问题、平曲线偏转左右判别问题、前缓和线段与后缓和线判别问题、桩号断链处理、设计缓和线不等长等问题均自动处理。
(5)计算误差一般在0.5mm以内。竖曲线段设计标高计算使用了平面解析几何方法推导的计算公式,计算精度可以满足工程施工规范要求。平曲线参数计算公式中程序将自动处理设计缓和线不等长时的相关曲线参数计算。
(6)全路线坐标计算程序,在基础参数输入时,只要求输入路线交点桩号,交点坐标X、Y值、曲线半径、缓和线长度等五个必需的参数。纯圆平曲线时,设计缓和线长度L输入0。平曲线前后设计缓和线等长时,输入设计缓和线长度L时,L值只输入一个数即可。平曲线前后设计缓和线不等长时,前后设计缓和线长度需合并输入L。由程序自动识别处理。(例如:设计缓和线等长L1=L2=85,L值输入85。设计缓和线不等长L1=85;L2=75,L值输入1085075。特别说明,此时的L1、L2都要以百位数输入,前面加1是为了方便程序处理)。
(7)三组程序中均考虑了桩号断链问题。如路线存在桩号断链,在程序使用前一定要修改好断链子程序中的断链桩号。如路线不存在桩号断链问题,只要将断链子程序中的断链桩号设定在路线以外即可,如:修改链桩号39350,变为939350或9939350。其它断链桩号修改方法类同,就跳开了断链问题。
3 程序使用说明
程序使用前计算器需设置为角度制。CASIO-5800P新的计算器需要首先自定义10个以上的可变存储器,才能正常运行程序。如首先使用了坐标计算程序,路线平曲线元素输入完成,再使用标高计算程序,依次完成竖曲线元素输入,这是理想的使用顺序,不会因操作问题丢失竖曲线元素数据。
三组程序总使用自定义变量存储器个数为:(Z[6]+1)×6+Z[5]×3。
Z[6]为路线平曲线交点个数,(桩号)M—Z[6K+7];(X坐标)A—Z[6K+8];(Y坐标)B—Z[6K+9];(半径)R—Z[6K+10];(设计缓和线)L—Z[6K+11];(ZH点桩号)ZH—Z[6K+12]。
Z[5]为路线竖曲线交点个数。标高计算程序的自定义存储器编号是在首先定义了平曲线个数基础上再向上递加的。C=Z[6]+1;(桩号)M—Z[6C+3K+1];(半径)R—Z[6C+3K+2];(JD标高)H—Z [6C+3K+3]。完成路线元素输入后,对照设计资料进行坐标或标高计算对比,正确无误后方可在工地现场使用。
4 程序编制原理
4.1 全路线坐标计算
(1)计算思路:判断计算点桩号是否小于ZH点桩号,如小于ZH点桩号(否则如大于ZH点桩号进行下一个ZH点桩号断)则确定桩号所在JD位置,进行参数赋值,计算曲线参数,计算ZH点、HY点、YH点、HZ点桩号,确定计算点桩号位置范围,调用对应的子程序计算坐标。
(2)计算步骤:输入计算点桩号→判断计算点的位置→确定计算桩号所在平曲线JD→曲线参数计算赋值→判断计算点在已确定的JD曲线上处于那个线段范围内→调用相关子程序进行中桩坐标计算→如需要进行需要的边桩坐标计算→完成计算后返回主程序进行下一个给定桩号的坐标计算。
(3)主要变量说明。程序要求输入的路线平曲线元素:起点坐标X、Y值;终点坐标X、Y值;各平曲线交点桩号、坐标X、Y值;平曲线半径R;平曲线设计缓和线长度L。
一般变量意义说明:左偏角I设置为1,右偏角I设置为-1;JD切线方位角F;计算点桩号Z;JD桩号M;曲线切线长度T(T1为T;T2为Z[12]);曲线总长度S;设计缓和线长度L(L1为L;L2为Z[10]);圆曲半径R;求算点桩号Z;边桩坐标计算判断符号Q,Q为边桩偏转中线角度。可计算任一偏转角度的边桩坐标。左边桩Q输入-90,右边桩Q输入90。边距为K,输入边桩距中线距离。程序输出相应边桩坐标。Q输入0,程序只计算中桩坐标。
4.2 全路线标高计算
(1)计算思路:计算切线长度,判断计算点桩号是否小于竖曲线起点桩号,如小于竖曲线起点桩号(否则如大于竖曲线起点桩号进行竖曲线起点桩号判断)则确定桩号所在JD位置,进行参数赋值,调用标高计算子程序进行标高计算。
程序要求输入的路线竖曲线元素:起点桩号;起点桩号设计标高;终点桩号;终点桩号设计标高;各竖曲线交点桩号、交点标高;竖曲线半径。
一般变量意义说明:交点桩号M,交点标高H;竖曲线半径R;后纵坡度I;前纵坡度J;凸竖曲线D设置为1,凹竖曲线D设置为-1;竖曲线切线T。
(2)计算步骤:输入计算点桩号→判断计算点的位置→确定计算桩号所在竖曲线JD→判断计算点在已确定的JD曲线上处于那个线段范围内→调用相关子程序进行中桩标高计算→如需要进行需要的边桩标高计算→完成计算后返回主程序进行下一个给定桩号的坐标计算。
(3)竖曲线段标高计算公式的建立:将路线展开纵断面翻转90°视为一水平面,建立大地相对坐标系:路线里程设为X轴,高程设为Y轴,假定路线起点K0+000与高程为0.000的点为坐标系的原点(0,0)。竖向坐标值(高程值):
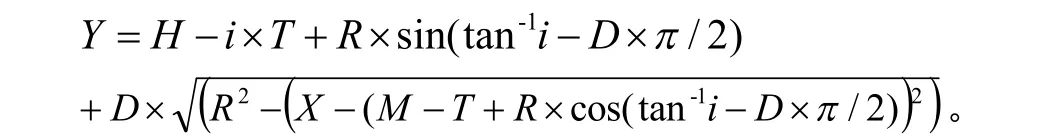
4.3 全路线坐标反算桩号计算
程序变量设置与全路线标高计算相同,部分子程序共用。
(1)计算思路:判定计算点所在最近JD后,首先在临近三个JD计算判断投影点是否在圆上,如果是,完成计算。否则判断是否在本JD前或后直线段上,如果是,完成计算。否则一定在本交点或前或后缓和线上,完成计算即可。
(2)基本计算原理:基本计算原理如图1,2,3,4说明:
(3)计算步骤。输入求算点坐标X,Y→判断求算点的位置→确定计算点最近平曲线JD→曲线参数计算准备,圆心坐标计算→判断求算点是否在本交点圆曲线段,如在计算桩号及位置→否则同理计算前后曲线参数判断是否在前后交点的圆上,如在,计算投影点在圆曲线上的桩号及位置→否则计算点到JD后切线的距离Q值和计算点在切线上的投影点到交点的距离K值→K>0,说明点在交点后方。否则在前方。→判断投影点是否在直线段上(交点前或后由K>0或K<0自动处理),如在计算投影点在直线段上的桩号及位置→否则解算点在缓和线上的缓和线长度(交点前或后由K>0或K<0自动处理)→计算投影点在缓和曲线上的缓和线上的桩号及点到缓和线的(左或右)距离→返回开始下一个坐标点的桩号计算。
主要公式
点到直线距离:设求算点坐标(C,D);JD坐标(A,B);求算点到切线距离Q=(C-A)sin(F-180)-(D-B)cos(F-180);求算点投影点到JD距离为K=(C-A)sin(F-90)-(D-B)cos(F-90)。
圆上的投影点计算:计算圆心坐标→计算圆心至HY点、圆心至YH点方位角。→计算圆心至求算点方位角。→判断圆心至求算点方位角指向范围是否在圆上。
缓和线段解算方程求解投影点的缓和线长度:
设计算点坐标为(T-K,Q):X=W-W^5/(40×R2×L2)-①;Y= W^3÷(6RL)-②;Y=tan(90+90W2/(RLπ)×(X-T+ABS(K))+Q-③解方程组①、②与③得到求算点投影点缓和线上的缓和线长度W。
5 程序操作说明
5.1 全路线坐标计算程序
程序名:主程序QLXZB-JS;
相关子程序10个:平曲线元素输入LXYS-SR;单曲路线坐标计算LX-ZB-JS;平曲交点赋值JSJDFZ;曲线参数计算QX-CS;圆曲线段坐标计算YQX-ZB-JS;缓和曲线段坐标计算HQS-ZB-JS;直线段坐标计算Q-ZXD-ZB-JS;方位角计算FWJJS;桩号断链处理DL--CL;边桩坐标计算BZ。
程序输入变量说明:重新输入或校对路线平曲线元素,LSYSSR=0?输入0,否则回车进行桩号输入。Z[6]-路线平曲线交点个数N (包括路线起点BP;路线终点EP;)。平曲线元素输入时,首先要求输入的是起点BP、终点EP点坐标(起点桩号、终点桩号不需输入),后续n=2时输入JD1的M—桩号;A—坐标X值;B—坐标Y值;R—半径;L—缓和线长(特别说明:当曲线为单圆曲线时L输入0,平曲线前后设计缓和线等长时,输入设计缓和线长度L时,L值只输入一个数即可,平曲线前后设计缓和线不等长时,前后设计缓和线长度合并输入L即可。例如:设计缓和线等长L1=L2=180,L值输入180。设计缓和线不等长L1=180;L2=160,L值输入1180160。此时的L1、L2都要以百位数输入,前面加1是方便程序处理)。以此类推。
Z—输入计算点桩号;Q—输入计算点在前进方向的转角,中桩坐标计算完成后,如果不需要计算边桩坐标则Q输入0,否则Q输入相应边桩偏转角(如边桩在路线中线左侧90度,则Q输入-90;边桩在路线中线右侧60度输入则Q输入60)。K—输入计算点边距(边桩至路线中桩的水平距离)。
程序计算主要中间变量说明:
G—路线偏转角度;O—缓和线偏转角度;L—设计缓和线长度; F—JD后方位角;E—JD前方位角;T—切线长度;S—曲线长度;Z[7]—断链长度;Z[10]—平曲线第2设计缓和线长度;Z[11]—平曲线第2缓和线偏转角度;Z[12]—平曲线第2切线长度。
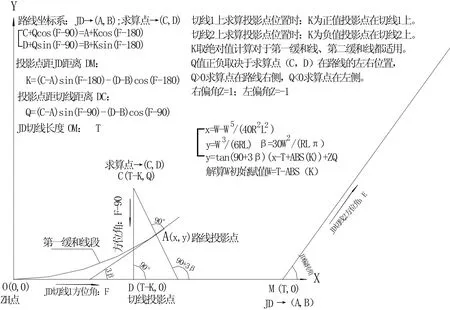
图1 平曲线第1缓和线段计算原理示意图
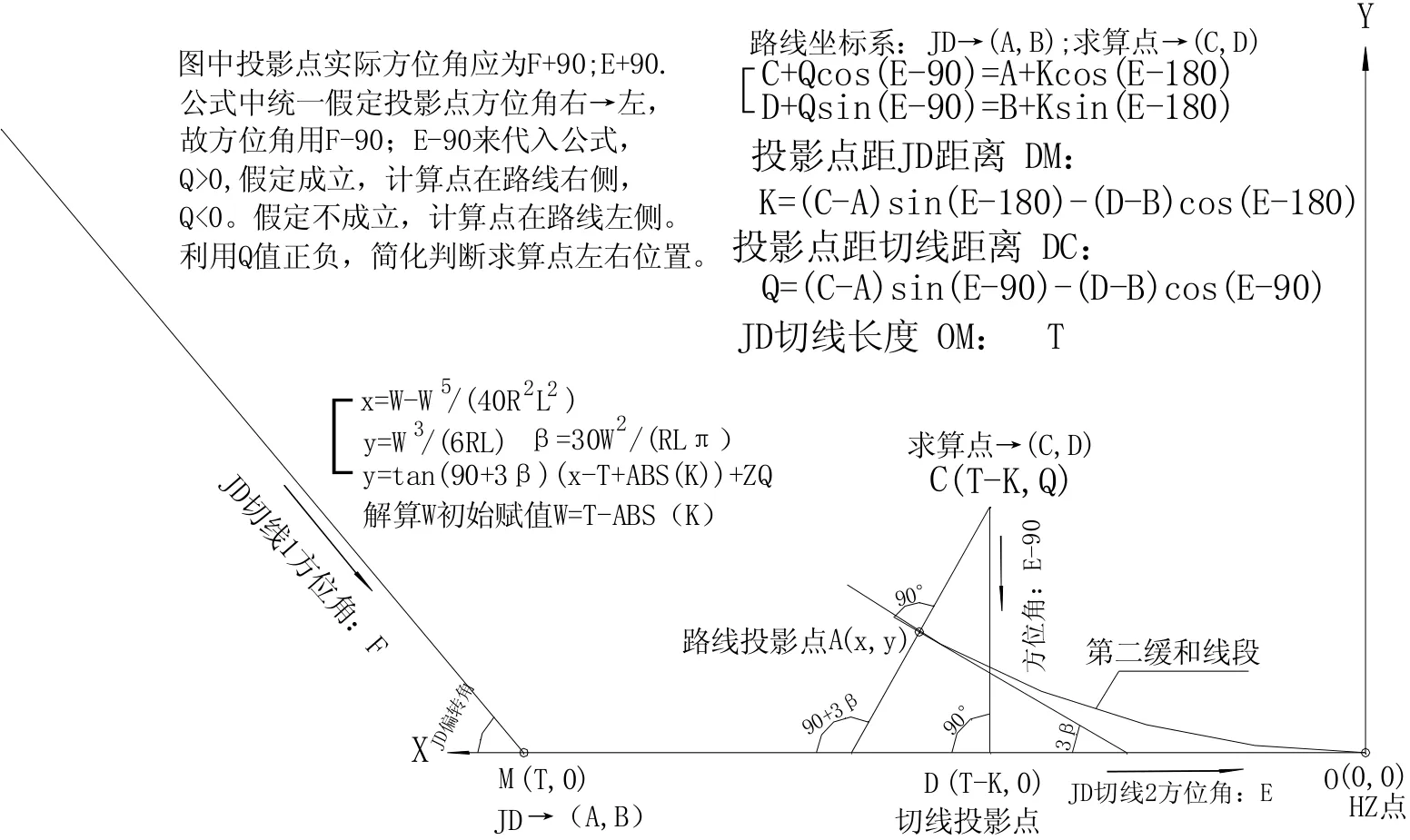
图2 平曲线第二缓和线段计算原理示意图
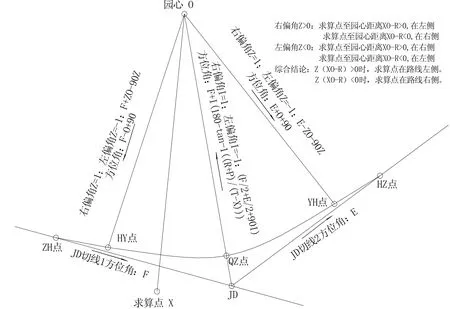
图3 平曲线左偏角圆曲线段计算原理示意图
坐标输出"Z.X"表示在直线段上的中桩X值;输出"Z.Y"表示在直线段上的中桩Y值;输出"Y.X"表示圆曲线段上的中桩X值;输出"Y.Y"表示在圆曲线段上的中桩Y值;输出"H.X"表示在缓和曲线段上的中桩X值;输出"H.Y"表示在缓和曲线段上的中桩Y值。
5.2 全路线标高计算程序
程序名:主程序BGQLX-JS;
相关子程序5个:竖曲线元素输入SQXYS-SR;单曲线标高计算GB-JS(角度制);标高计算要素赋值BGYSFZ;断链纵坡处理ZP--CL;断链标高处理BG--CL;
程序输入变量说明:重新输入或校对路线元素,SQXYSSR=0?输入0,否则回车进行桩号输入。Z[5]-路线竖曲线交点个数N (包括路线起点BP;路线终点EP;)。竖曲线元素输入时,首先要求输入的是BP、EP点桩号、标高,后续n=2时输入JD1的M—桩号;H—标高;R—竖曲线半径。以此类推。
Z—输入求算点桩号;中桩标高计算完成后,如果不需要计算边桩标高横坡度H-PO?输入0,否则输入道路横坡度(如:1.5%输入1.5),S—输入计算点边距。
程序计算主要中间变量说明:Z[6]-路线平曲线交点个数;C=Z [6]+1;T—切线长度。
5.3 全路线坐标反算桩号计算程序
程序名:主程序ZB-FS-ZH
相关子程序6个:圆坐标反算YZBFS;点到直线距离DDZXJL;平曲交点赋值JSJDFZ;曲线参数计算QX-CS;桩号断链处理DL—CL;桩号断链处理DL--CL2。
程序输入变量说明:求算点坐标X→C;Y→D。在执行过全路线坐标计算程序且已完成路线平曲线元素输入后,才能运行全路线坐标反算桩号计算程序。
6 程序清单
清单中的除号“/”,在计算器程序输入时输入“÷”。
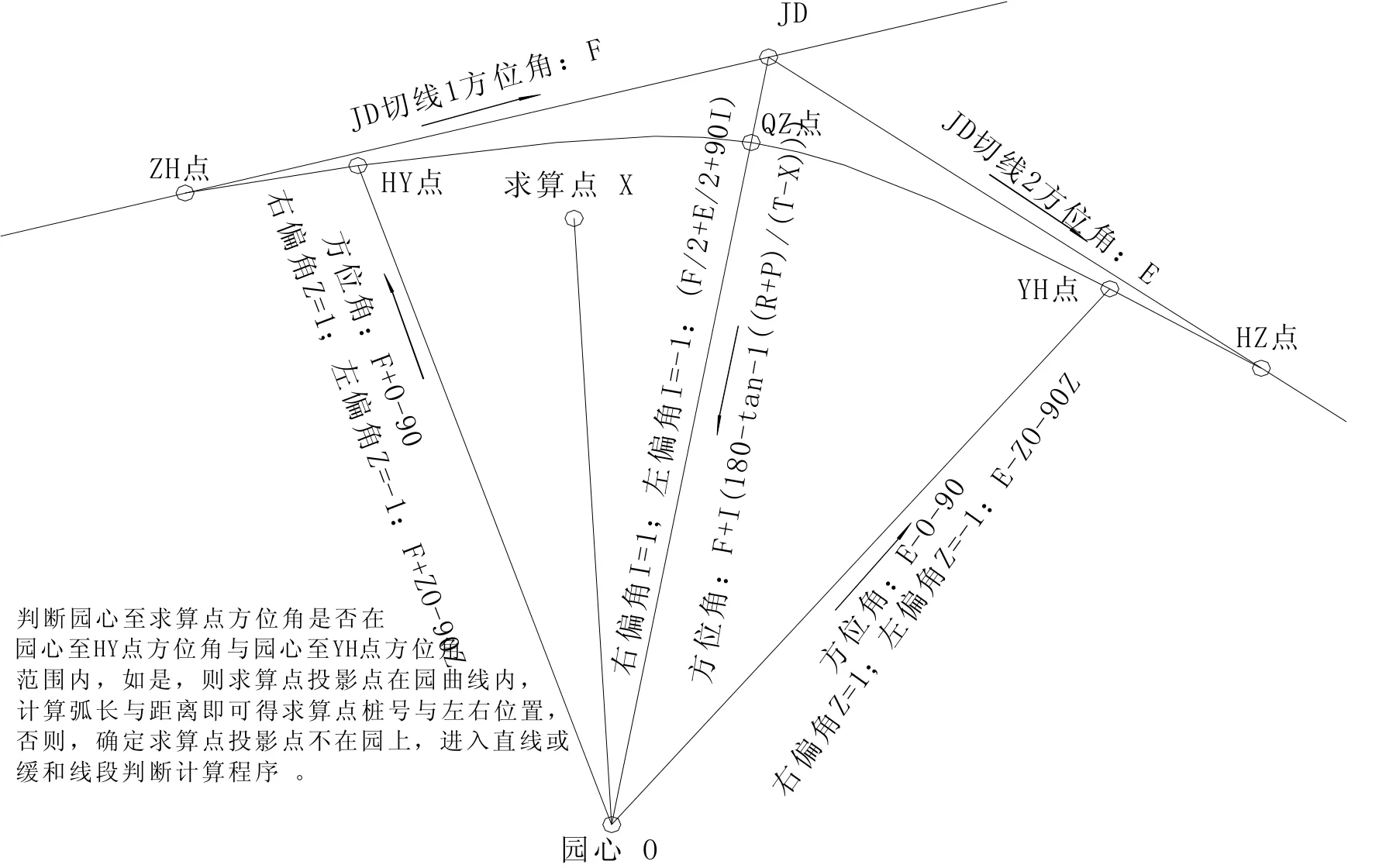
图4 平曲线右偏角圆曲线段计算原理示意图
6.1 CASIO-5800程序清单。
全路线坐标计算:QLXZB-JS
"LXYS-SR=0"?K:K=0=>Prog"LXYS-SR":LbI1:"Z"?Z: Z[6]→N:For1→KToN-2:IfK<N-2:ThenIfZ≤Z[6(K+1) +12]:ThenProg"JSJDFZ":Goto2:ElseGoto3:IfEnd:IfEnd: Prog"JSJDFZ":Goto2:LbI3:Next:LbI2:H→K:Prog"LX-ZBJS":K→H:Goto1
平曲线元素输入:LXYS-SR
Z[6]→N:"N"?N:6(N+1)→DimZ:N→Z[6]:Z[8]→M:"BP-X"?M:M→Z[8]:Z[9]→M:"BP-Y"?M:M→Z[9]:Z[6(N-1)+8]→M: "EP-X"?M:M→Z[6(N-1)+8]:Z[6(N-1)+9]→M:"EP-Y"?M:M→Z[6(N-1)+9]:For1→KToN-2:"n=":K+1Z[6K+7]→M: "JD"?M:M→Z[6K+7]:Z[6K+8]→A:"A"?A:A→Z[6K+8]:Z[6K+9]→B:"B"?B:B→Z[6K+9]:Z[6K+10]→M:"R"?M:M→Z[6K+10]: Z[6K+11]→M:"L"?M:M→Z[6K+11]:Next:For1→KToN-2: Prog"JSJDFZ":Prog"QX-CS":M-T→Z[6K+12]:Next:Return
平曲交点赋值:JSJDFZ
Z[6K+7]→M:Z[6K+8]→A:Z[6K+9]→B:Z[6K+10]→R:Z [6K+11]→L:A→X:B→Y:Z[6(K-1)+8]→A:Z[6(K-1)+9]→B: Prog"FWJJS":J→F:X→A:Y→B:Z[6(K+1)+8]→X:Z[6(K+1)+9]→Y:Prog"FWJJS":J→E:E-F→G:1→I:G<0=>-1→I:Abs(G)→G:Return
方位角计算:FWJJS
Pol((X-A),(Y-B)):J<0=>360+J→J:Return
桩号断链处理:DL—CL
39350-39311.265→Z[7]:IfZ≥39350ANDZ<39508.004: ThenZ→X:Z-Z[7]→Z:IfEnd:Return
单曲路线坐标计算:LX-ZB-JS
Prog"DL--CL":Prog"QX-CS":M-T→Z[1]:Z[1]+L→Z[2]: Z[1]+S→Z[4]:Z[4]-Z[10]→Z[3]:IfZ≤Z[1]OrZ≥Z[4]:Then Prog"Q-ZXD-ZB-JS":Goto1:ElseIfZ≤Z[3]ANDZ≥Z[2]:Then Prog"YQX-ZB-JS":Goto1:IfEnd:IfEnd:Prog"HQS-ZB-JS": LbI1:Return
曲线参数计算:QX-CS
L→Z[10]:90L/(Rπ)→Z[11]:IFL>999:ThenL-INT(L/ 1000)*1000→Z[10]:INT(L/1000)-1000→L:IfEnd:90L/(Rπ)→O:L2/(24R)-L^(4)/(2688R^(3))→P:L/2-L^(3)/(240R2)→X :90Z[10]/(Rπ)→Z[11]:X+Rtan(G/2)-P/tan(G)+(Z[10]2/(24R)-Z[10]^(4)/(2688R^(3)))/sin(G)→T:Z[10]/2-Z[10]^(3)/(240R2) +Rtan(G/2)-(Z[10]2/(24R)-Z[10]^(4)/(2688R^(3)))/tan(G)+P/sin (G)→Z[12]:(G-O-Z[11])πR/180+L+Z[10]→S:√((L-L^(3)/ (40R2))2+(L2/(6R))2)→V:Return
直线段坐标计算:Q-ZXD-ZB-JS
IfZ<M-T:Then1→H:180+F→E:A+Tcos(E)→C:B+Tsin (E)→D:M-T-Z→W:Else-1→H:A+Z[12]cos(E)→C:B+Z[12] sin(E)→D:Z-(M-T+S)→W:IfEnd:"Z.X=":C+Wcos(E)→X"Z.Y=":D+Wsin(E)→Y"Q"?Q:IfH>0:ThenF+Q→N: ElseE+Q→N:IfEnd:Prog"BZ":Return
缓和曲线段坐标计算:HQS-ZB-JS
1→H:Z>M=>-1→H:IfH>0:ThenZ-(M-T)→W:A+Tcos (F+180)→C:B+Tsin(F+180)→D:F→E:Goto3:IfEnd:(M-T+S)-Z→W:A+Z[12]cos(E)→C:B+Z[12]sin(E)→D:E+180→E:Z[10]→L:Lb13:30HIW2÷(RLπ)→U:W-W^(5)÷(40R2L2)→X:W^(3) ÷(6RL)→Y:√(X2+Y2)→W:C+Wcos(U+E)→X:"H.X=": XD+Wsin(U+E)→Y:"H.Y=":Y"Q"?Q:IfH>0:Then F+3U+Q→N:ElseE-180+3U+Q→N:IfEnd:Prog"BZ":Return
圆曲线段坐标计算:YQX-ZB-JS
A+Tcos(F+180)→C:B+Tsin(F+180)→D:C+Vcos(F+IO/3)→C:D+Vsin(F+IO/3)→D:90(Z-(M-T+L))/R/π→U:2RsinU→W:IU+F+IO→N:C+WCosN→X:"Y.X=":XD+WsinN→Y:"Y.Y=":Y"Q"?Q:F+2IU+IO+Q→N:Prog"BZ":Return
边桩坐标计算BZ
全路线标高计算:BGQLX-JS
"SQXYS-SR=0"?K:K=0=>Prog"SQXYS-SR":LbI1:Z[6] +1→C:"Z"?Z:Z[5]→N:
For1→KToN-2:IfK<N-2:ThenK+1→K: Prog"BGYSFZ":K-1→K:IfZ≤Z[6C+3(K+1)+1]-T:Then Prog"BGYSFZ":Goto2:ElseGoto3:IfEnd:IfEnd:
Prog"BGYSFZ":Goto2:LbI3:Next:LbI2:Prog"GB-JS": Goto1
竖曲线元素输入:SQXYS-SR
Z[5]→N:"N"?N:Z[6]+1→C:6C+3N→DimZ:N→Z[5]:Z [6C+1]→M:"BP-M"?M:M→Z[6C+1]:Z[6C+3]→M:"BP-H"?M: M→Z[6C+3]:Z[6C+3(N-1)+1]→M:"EP-M"?M:M→Z[6C+3(N-1)+1]:Z[6C+3(N-1)+3]→M:"EP-H"?M:M→Z[6C+3(N-1)+3]: For1→KToN-2:"n=":K+1Z[6C+3K+1]→M:"JD"?M:M→Z[6C+3K+1]:Z[6C+3K+3]→H:"H"?H:H→Z[6C+3K+3]]:Z [6C+3K+2]→R:"R"?R:R→Z[6C+3K+2]:Next:Return
标高计算要素赋值:BGYSFZ
0→U:0→P:Z[6C+3K+1]→M:Z[6C+3K+3]→H:Z[6C+3K+2]→R:Prog"ZP--CL":(H-Z[6C+3(K-1)+3])/(M-Z[6C+3(K-1) +1]-U)→I:(Z[6C+3(K+1)+3]-H)/(Z[6C+3(K+1)+1]-M-P)→J: tan-1(I)-tan-1(J)→W:Rtan((Abs(W))/2)→T:Return
断链纵坡处理:ZP—CL
39350-39311.265→Z[7]:39350>Z[6C+3(K-1)+1]AND39350<M=>Z[7]→U:
39350>MAND39350<Z[6C+3(K+1)+1]=>Z[7]→P:Return
断链标高处理:BG—CL
Z≥39350ANDZ<39548.043=>Z-Z[7]→Z:Return
单曲线标高计算:GB-JS(角度制)
Prog"BG--CL":tan-1(I)-tan-1(J)→W:(AbsW)/W→D: Rtan((Abs(W))/2)→T:tan-1(I)-90D→C:IfZ<M-T:"X=":Then H-I(M-Z)Goto1:ElseIfZ>M+T:then"X=":H+J(Z-M)Goto1:IfEnd:IfEnd:"X=":H-TI+RSinC+D√(R2-(Z-(MT+RCosC))2)LbI1:"H-PO="?V:IfV≠0:Then"S="?Q: Ans-0.01VQIfEnd:Return
坐标反算桩号:ZB-FS-ZH
LbI1:"C"?C:"D"?D:Z[8]-C→A:Z[9]-D→B:Pol(A,B):I→U:1→Z[3]:Z[6]→N:For1→KToN-2:Z[6K+8]-C→A:Z [6K+9]-D→B:Pol((A,B):I<U=>K→Z[3]:I<U=>I→U:Next:1→H:Z[3]≠1=>Z[3]-1→K:Prog"YZBFS":0=U=>Goto1:Z[3]≠1=>M-T+S→Z[6(Z[6]-1)+12]:Z[6]-2≠Z[3]=>Z[3]+1→K: Prog"YZBFS":0=U=>Goto1:Z[3]→K:Prog"YZBFS":0=U=>Goto1:Z[6(Z[3]+1)+12]→Y:Z[6(Z[6]-1)+12]→U:Z[3]=1=>Z [18]-99999→U:Z[6]-2=Z[3]=>Z[6(Z[6]-2)+7]+99999→Y:F→X: E→F:Prog"DDZXJL":X→F:K→X:Prog"DDZXJL":IfK<0: ThenIfAbs(X)>Y-M+T+Z[12]-S:ThenZ[3]+1→K:Goto3: Else-1→H:Goto4:IfEnd:ElseIfK>M-U:ThenZ[3]-1→K:-1→H:Goto3:ElseGoto5:IfEnd:IfEnd:LbI3: Prog"JSJDFZ":Prog"QX-CS":I→Z:LbI4:-1=H=>E→F: Prog"DDZXJL":LbI5:IfK>0ANDAbs(K)≥TorK<0AND Abs(K)≥Z[12]:ThenIfK>0:ThenM-Abs(K)→X:X-Z[7]→Z:Prog"DL--CL2":ElseM+Abs(K)-T-Z[12]+S→X:X+Z[7]→Z:Prog"DL--CL":IfEnd:"ZHUANG.HAO-Z":XIfQ>0: Then"Y-C":Else"Z-C":IfEnd:Abs(Q)Goto1:IfEnd:W→X:LbI2:(W^3÷(6RL)-ZQ)/tan(90+90W2/(RLπ))+T-ABS(K) +W^5÷(40R2L2)→X:IfABS(X-W)>0.0001:ThenX→W:Goto 2:IfEnd:X→W:W-W^5÷(40R2L2)→X:W^3÷(6RL)→Y:IfK>0:Then"ZHUANG.HAO-H1":M-T+WElse"ZHUANG. HAO-H2":M-T+S-WIfEnd:IfQ>0:Then"Y-C":Else"ZC":IfEnd:√((T-Abs(K)-X)2+(ZQ-Y)2)Goto1:
点到直线距离:DDZXJL
(C-A)sin(F-180)-(D-B)cos(F-180)→Q:(C-A)sin(F-90)-(D-B)cos(F-90)→K:T-ABS(K)→W:-1=H=>Z[10]→L:Return
圆坐标反算:YZBFS
Prog"JSJDFZ":Prog"QX-CS":√((T-X)2+(R+P)2)→H: F+I(180-tan-1((R+P)/(T-X)))→N:I→Z:F+ZO-90Z→X:X>360=>X-360→X:X<0=>360+X→X:E-ZZ[11]-90Z→Y:Y>360=>Y-360→Y:Y<0=>360+Y→Y:IfZ>0:ThenX>Y=>Y+360→Y:ElseY>X=>X+360→X:IfEnd:C-A-Hcos(N)→I:DB-Hsin(N)→J:Pol(I,J):J<0=>360+J→J:IfY≥JANDJ≥X OrY≤JANDJ≤XOrY≥J+360ANDJ+360≥XOrY≤J+360ANDJ+360≤X:Then"ZHUANG.HAO-Y":X>360=>X-360→X:IfZ>0:ThenX>J=>J+360→J:ElseJ>X=>X+360→X:IfEnd:M-T+L+Abs(J-X)Rπ/180If(I-R)Z<0:Then"YC":Else"Z-C":IfEnd:Abs(I-R)0→U:IfEnd:Return
桩号断链处理DL--CL2
IfZ>39235.639ANDZ≤39311.265:ThenZ→X:IfEnd: Return
6.2 由于篇幅所限,本文暂略CASIO-4800 /CASIO-4850程序清单
7 桩号断链子程序修改示例说明
为便于断链桩号修改,将断链处理问题集中在四个子程序中。现以S218线哈-苏段HSZD-2标段K36+000~K42+000右幅设计资料计算示例。
断链桩号K39+350=K39+311.265,桩号短链28.735m(同理,如路线为长链,计算方法相同,Z[7]为负值)。断链桩号后平曲线终点桩号为39235.639(39235.639小于断链桩号);断链桩号前平曲线起点桩号为39508.004(39508.004大于断链桩号);断链桩号前竖曲线起点桩号为39548.043(39548.043大于断链桩号);为了直观,直接采用实际桩号数据修改子程序。
修改四个断链处理子程序如下:
桩号断链处理DL—CL:39350-39311.265→Z[7]:IfZ≥39350 ANDZ<39508.004:ThenZ→X:Z-Z[7]→Z:IfEnd:Return。断链纵坡处理ZP—CL:39350-39311.265→Z[7]:39350>Z[6C+3(K-1)+1]AND39350<M=>Z[7]→U:39350>MAND39350<Z [6C+3(K+1)+1]=>Z[7]→P:Return。断链标高处理BG—CL:Z≥39350ANDZ<39548.043=>Z-Z[7]→Z:Return。桩号断链处理DL--CL2:IfZ>39235.639ANDZ≤39311.265:ThenZ→X: IfEnd:Return。
