基于PMF进行潜在特征因子分解的标签推荐

刘胜宗 樊晓平 廖志芳 吴言凤

摘要： 现有社会标签推荐技术存在数据稀疏、时间复杂度高以及可解释性低等问题，鉴于此，提出基于概率矩阵分解（PMF）进行潜在特征因子联合分解的标签推荐算法（TagRecUPMF），它结合用户、资源及标签3方面的潜在特征，联合构建对应的概率形式的潜在特征向量，然后根据它们两两之间的特征向量内积进行线性组合，从而产生TopN推荐。该算法解决了数据规模大且稀疏情况下的精度问题，算法的线性复杂度使得其可用于大规模数据。实验结果表明，相比于TagRecCF，PITF， TTD，Tucker，NMF等算法，本文算法既提高了推荐的准确率，又降低了时间损耗。与PITF算法相比较，准确率得到了提高，而处理时间相差不明显；与TTD算法相比较，在准确率相差不明显的情况下，大大降低了时间损耗。因此，本文的TagRecUPMF算法相比其他算法表现出了一定的优势。

关键词：协同过滤；潜在特征因子；标签推荐；推荐系统；概率矩阵分解

中图分类号：TN911。23 文献标识码：A

作为Web2。0的重要特征，社会标签系统允许用户对系统资源利用个性化标签进行标注，从而使具有相同兴趣偏好的用户相互推荐及共享资源＼[1＼]。国内外知名社会标签系统有音乐类标签系统last。fm＼[2＼]、图片类标签系统flickr＼[3＼]、电影类标签系统movielens＼[4＼]、书签和出版物信息共享系统bibsonomy＼[5＼]等。这些网站采用社会标签整合各类资源，这有助于用户组织、浏览和搜索自己感兴趣的资源，也能够更好地帮助用户之间进行沟通及共享，而标签推荐系统可将用户感兴趣的标签推荐给使用同一资源的用户＼[6＼]。

标签推荐系统基于用户以往的标注行为进行标签推荐，这种推荐同时依赖于用户和资源＼[7＼]。目前广泛应用的协同过滤推荐＼[8＼]（CF）为目标用户寻找有相似标注行为的其他用户（近邻），并将近邻在目标资源上标注过的其他标签推荐给目标用户，该技术简单和实用，但也面临着冷启动和数据稀疏问题＼[6＼]。基于此，研究者尝试从其他角度去研究新的推荐策略及方法，目前，大部分关于标签推荐的研究集中在因子分解方面，比较典型的有非负矩阵分解（NMF）＼[9＼]，奇异值分解（SVD）＼[10＼]，高阶奇异值分解（HOSVD）＼[6＼]，Tucker张量分解＼[8＼]，PITF张量分解＼[1＼]以及TTD张量分解＼[6＼]，这些方法在解决数据稀疏性和缺失值带来的问题上取得了较好的效果。但这些分解技术仅考虑了标注关系，并未考虑用户的评分偏好关系，由于用户选择标签进行标注的过程中同时受自身对资源和标签的兴趣偏好影响。另外，不同用户对标签或资源的兴趣偏好侧重面不一样[11]，标签和资源是受某些基本的、潜在的特征支配，用户的偏好则是由用户对这些潜在特征喜好程度的加权综合，用户的标注行为除受本身偏好的影响之外，同样还受到标签和资源的潜在特征结构的影响＼[8＼]。这体现出一种“资源标签”的双重概率关系＼[12＼]，这种关系同样存在于“用户资源”、“用户标签”情形中。为了解决上述问题，本文提出一种新的标签推荐方法（TagRecUPMF），该方法采用概率矩阵分解技术进行潜在特征因子联合分解，然后通过潜在特征向量之间相互组合完成推荐。

湖南大学学报（自然科学版）2015年

第10期刘胜宗等：基于PMF进行潜在特征因子分解的标签推荐

1问题定义

社会标签系统可形式化定义为F：=（US，TS，IS，RS），其中US为User集合，TS为Tag集合，IS为Item集合，RS为User，Item和Tag之间的关系集合，其中RS∈TS×US×IS＼[6＼]。标签推荐是在用户访问的资源上推荐与资源相关的标签。符号标记如表1所示。

表1符号标记表

Tab。1Definition table of symbol

符号标记

解释说明

US={u1，u2，…，um}

用户集合，共m个用户

IS={i1，i2，…，in}

资源集合，共n个资源

TS={t1，t2，…，to}

标签集合，共o个标签

U∈Rl×m

用户潜在特征矩阵

V∈Rl×n

资源潜在特征矩阵

W∈Rl×o

标签潜在特征矩阵

l∈R

潜在特征空间维数

B={bui}，B∈Rm×n

用户资源关系矩阵

C={but}，C∈Rm×o

用户标签关系矩阵

A={ait}，A∈Rn×o

资源标签关系矩阵

一般地，用户对标签的认可程度、用户对资源的兴趣程度和资源与标签的关联程度分别表示成用户标签认可关系矩阵C、用户资源兴趣矩阵B和资源标签关联度矩阵A。l表示潜在特征空间的维数。用户对标签的认可程度由用户潜在特征向量和标签潜在特征向量的内积得到，用户对资源的兴趣程度由用户潜在特征向量和资源潜在特征向量的内积得到，资源与标签的关联度由资源潜在特征向量和标签潜在特征向量的内积得到。

设用户u访问资源i时，选择标签t的概率表示为yu，i，t，那么

yu，i，t=f（UTuVi，UTuWt，VTiWt）。（1）

式中：Uu为用户u的潜在特征向量；Vi为资源i的潜在特征向量；Wt为标签t的潜在特征向量；UTuVi，UTuWt，VTiWt分别用于计算用户u对资源i的感兴趣程度、用户u对标签t的认可程度以及标签t与资源i的关联程度；f（·）参数为UTuVi，UTuWt，VTiWt的函数；yu，i，t又称为给定用户u和资源i情况下的标签t的推荐概率。

当用户u在访问资源i时，标签的TopN推荐列表可以定义如下＼[6＼]：

Top（u，i，N）：=argmaxNt∈T（yu，i，t）。（2）

式中：N为推荐列表的长度。

2基于UPMF的标签推荐模型

本文提出基于联合概率矩阵分解（UPMF）的标签推荐算法TagRecUPMF，算法包含3个部分：

1）求解潜在特征向量。首先根据训练数据集计算实体间的关系矩阵，然后根据分解算法通过梯度下降方法，以最大化联合的后验概率为目标函数，学习得到用户潜在特征向量、资源潜在特征向量以及标签潜在特征向量。

2）根据公式（3）对给定的用户和资源计算标签集中各标签的推荐概率。

yu，i，t=βUTuVi+γUTuWt+δVTiWt，

s。t。β+γ+δ=1。（3）

3）根据TopN推荐规则，选取推荐概率排名前N的标签推荐给用户。

2。1实体间关系矩阵的计算

1）用户资源关系矩阵。用户资源关系矩阵B表示m个用户对n个资源的兴趣对应关系。B中元素bui表示用户u对资源i感兴趣的程度。

bui=αg（hui）+（1-α）g（rui）。 （4）

式中：hui为资源i被用户u标注的次数；rui为用户u对资源i的评分；g（·）为logistic函数，用于归一化；α为平衡因子，取值为＼[0，1＼]。

2）用户标签关系矩阵。用户标签关系矩阵C表示m个用户对o个标签的偏好对应关系。C中每个元素cut表示用户u对标签t的偏好或者认知程度。

cut=g（λut）。（5）

式中：λut为用户u使用标签t的次数。

3）资源标签关系矩阵。资源标签关系矩阵A表示n个资源和o个标签的关联度关系。A中元素ait表示资源i和标签t之间的关联程度，通常认为，在资源i上标注标签t的次数越多，表示有越多的用户认为标签t和资源i的关联度大。ait由公式（6）计算得到：

ait=g（τit）。（6）

式中：τit为资源i上标注标签t的次数。

2。2概率矩阵联合分解

TagRecUPMF标签推荐模型的概率图如图1所示。

图1TagRecUPMF的概率图模型

Fig。1Probabilistic graphical model of TagRecUPMF

其中，用户潜在特征向量Uu由用户标签关系信息和用户资源关系信息共享；资源潜在特征向量Vi则由用户资源关系信息和资源标签关系信息共享；标签潜在特征向量Wt由用户标签关系信息和资源标签关系信息共享。

概率矩阵分解模型中，首先假设潜在特征向量Uu，Vi，Wt的先验服从均值为0的高斯分布，即

p（U|σ2U）=∏mu=1N（Uu|0，σ2UI）；（7）

p（V|σ2V）=∏ni=1N（Vi|0，σ2VI）；（8）

p（W|σ2W）=∏oi=1N（Wt|0，σ2WI）。（9）

在给定用户u，资源i的潜在特征向量（维数为l）Uu，Vi后，用户u对i的感兴趣程度bui满足均值为g（UTuVi），方差为σ2B的高斯分布并相互独立，因此B的条件概率分布为：

p（B|U，V，σ2B）=∏mu=1∏ni=1[N（bui|g（UTuVi），σ2B）]IBui。（10）

式中：IBui为指示函数，当用户u访问或标注过资源i时，其值为1，否则为0；g（ ·）为logistic函数，用于将UTuV归一化。

用户u对标签t的兴趣程度cut满足均值为g（UTuWt）方差为σ2C的高斯分布且相互独立，那么C的条件概率分布如下：

p（C|U，W，σ2C）=∏mu=1∏ot=1[N（cut|g（UTuWt），σ2C）]ICut。 （11）

其中，当用户u使用过标签t进行标注时，ICut为1，否则为0。

若资源i和标签t的关联度ait满足均值为g（VTiWt），方差为σ2A的高斯分布且相互独立时，A的条件概率分布为：

p（A|V，W，σ2A）=∏ni=1∏ot=1[N（ait|g（VTiWt），σ2A）]IAit。 （12）

其中，当资源i和标签t有关联时，IAit值为1，否则为0。

由图1可以推导出U，V，W的后验分布函数，该分布函数的自然对数形式如公式（13）所示。

公式（13）中，

瘙 綇 是不依赖于参数的常量。在概率矩阵分解模型中，需要最大化公式（13），这是一个无约束情况下的优化问题，该问题的求解等价于最小化公式（14）。

lnp（U，V，W|B，C，A，σ2W，σ2V，σ2U，σ2A，σ2C，σ2B）=

-12σ2B∑mu=1∑ni=1IBui（bui-g（UTuVi））2-

12σ2C∑mu=1∑ot=1ICut（cut-g（UTuWt））2-

12σ2A∑ni=1∑ot=1IAit（ait-g（VTiWt））2-

12σ2U∑mu=1UTuUu-12σ2V∑ni=1VTiVi-12σ2W∑ot=1WTtWt-

∑mu=1∑ni=1IBuilnσB-∑mu=1∑ot=1ICutlnσC-

∑ni=1∑ot=1IAitlnσA-l∑mu=1lnσU-l∑ni=1lnσV-

l∑ot=1lnσW+

瘙 綇 ；（13）

Ω（U，V，W，B，C，A）=12∑mu=1∑ni=1IBui（bui-

g（UTuVi））2+λC2∑mu=1∑ot=1ICut（cut-g（UTuWt））2+

λA2∑ni=1∑ot=1IAit（ait-g（VTiWt））2+

λU2‖U‖2F+λV2‖V‖2F+λW2‖W‖2F；（14）

ΩUu=∑ni=1IBui（g（UTuVi）-bui）g'（UTuVi）Vi+

λC∑ot=1ICut（g（UTuWt）-cut）g'（UTuWt）Wt+λUUu； （15）

ΩVi=∑mu=1IBui（g（UTuVi）-bui）g'（UTuVi）Uu+

λA∑ot=1IAit（g（VTiWt）-ait）g'（VTiWt）Wt+λVVi；（16）

ΩWt=λC∑mu=1ICut（g（UTuWi）-cut）g'（UTuWi）Uu+

λA∑ni=1IAit（g（VTiWt）-ait）g'（VTiWt）Vi+λWWt。 （17）

公式（14）中：λC=σ2Bσ2C；λA=σ2Bσ2A；λU=σ2Bσ2U；λV=σ2Bσ2V；λW=σ2Bσ2W；‖·‖2F表示F范数。公式（14）的局部最小值采用梯度下降法进行求解，参数Uu，Vi，Wt的梯度下降更新公式分别为公式（15）-式（17）。

2。3算法复杂度分析

在梯度下降法中，算法的时间开销主要取决于目标函数Ω及其相应的梯度下降更新公式。在标签标注数据和用户评分数据中，存在大量的缺失值，这导致A，B，C矩阵很稀疏，容易得出公式（14）目标函数的计算时间复杂度为O（ρBl+ρCl+ρAl），其中ρA，ρB，ρC分别表示3个实体关系矩阵A，B，C的非零元素数目。同理，梯度下降公式（15）-（17）的计算复杂度分别为O（ρBl+ρCl），O（ρBl+ρAl），O（ρCl+ρAl）。所以，算法的一步迭代过程中的计算复杂度为O（ρBl+ρCl+ρAl），这表示算法的时间复杂度随3个关系矩阵中观测数据数量呈正线性关系，意味着该算法可应用于大规模的数据。

3实验结果及分析

3。1实验设计

3。1。1数据集

本文选取目前标签推荐研究常用的201110M版movielens数据集，该数据集包含了2 113个用户，10 197部电影以及13 222个标签。

3。1。2算法性能评价指标

目前衡量推荐算法优劣需要同时考虑准确率和召回率，而准确率和召回率＼[12＼]指标往往是负相关的，因此为了综合考虑算法的性能，本文选用F1指标＼[12＼]来衡量算法的性能，F1指标定义见公式（18），其中Precision表示准确率，Recall表示召回率，其计算方法可参考文献＼[12＼]。F1越高，算法的性能越好。

F1=2·Precision×RecallPrecision+Recall。（18）

3。1。3实验设计

为了检验TagRecUPMF算法的推荐效果，本文需要通过实验解决以下几个方面的问题：1）潜在特征向量的维度l对推荐性能的影响；2）平衡因子α对推荐结果的影响；3）参数λA和λC对推荐结果的影响；4）TagRecUPMF算法与现有经典标签推荐算法的准确度及时间效率比较。

实验前，为了比较不同数据规模和稀疏情况下算法的效果，分别从实验数据中抽取90%，70%，50%，30%作为训练集，其余作为测试集进行实验。

实验过程中，通过对训练集尝试不同的参数值，进而在测试集上得到F1指标值。经反复测试得出参数设为α=0。4，β=γ=δ=1/3，λC=1，λA=0。6， λU=λV=λW=0。05时，算法的效果最优。在后续的实验中，若无特别说明，这些参数均设为最优值。同时实验中，TopN推荐中取N=10。

3。2实验分析

3。2。1参数l对推荐性能的影响

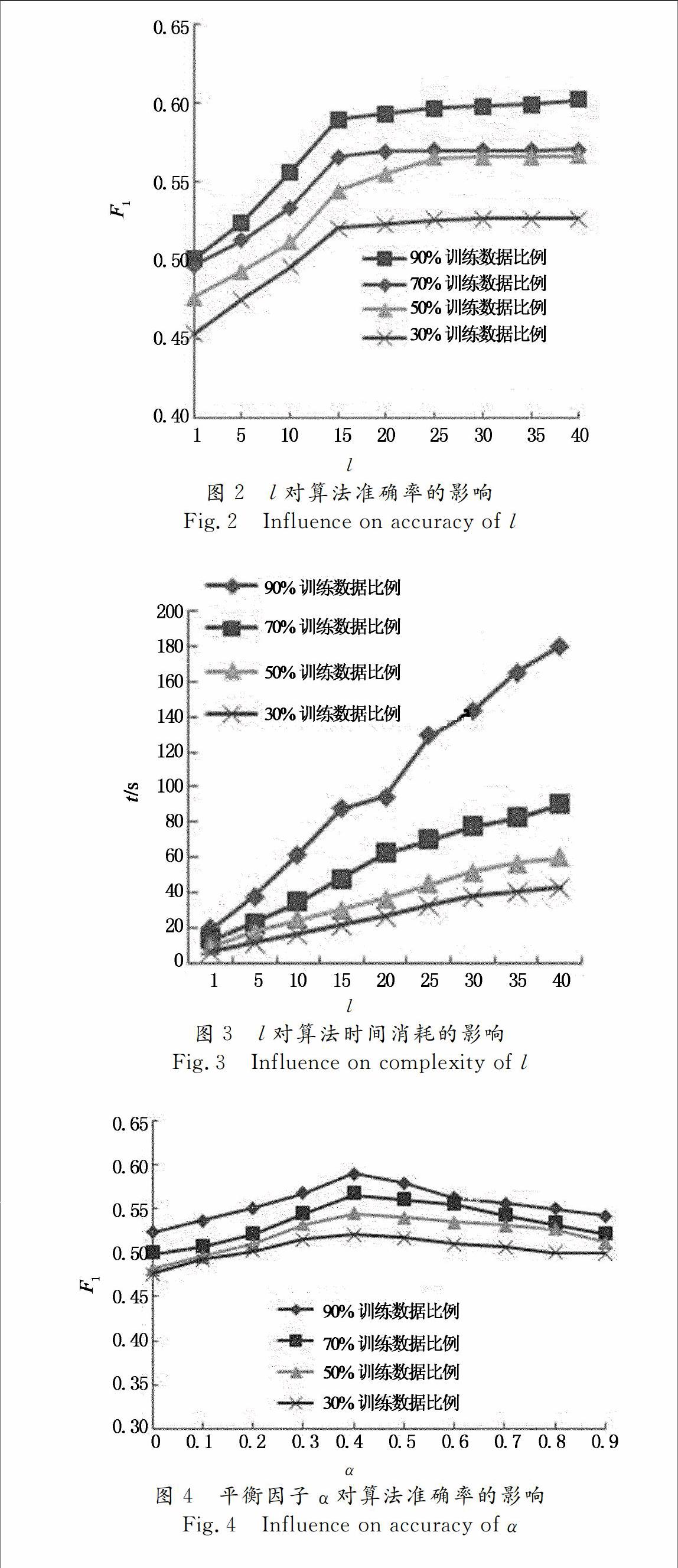
该实验用于检测潜在特征向量的维数l对推荐算法性能的影响。图2为l对算法准确率的影响，图3为l对算法时间效率的影响。从图2可以看出，随着特征向量维数的增加，推荐准确率慢慢提高，这说明增加潜在特征向量的维数可以提高矩阵分解算法的准确性，而当l>15时，精度增加的趋势变缓。由图3可以看出，随着l的增大，算法耗费的时间也成正比的增大。因此出于准确率和时间损耗的平衡考虑，选择l=15。

3。2。2α对推荐准确率的影响

在式（4）中，利用参数α来调节资源被标注次数和资源评分在用户对资源兴趣程度中的权重比例，从而影响推荐准确率。实验结果如图4所示。由图4可以看出，α值处于0。3到0。5之间时，F1的值由上升转变为下降趋势，这就意味着在这2个值之间存在一个可以使得F1最优的α值。本文将α值选取为0。4。这说明利用资源被标注次数和资源评分的加权组合来表示用户对资源兴趣程度时的效果略好于这两者单独表示的情况。

l

图2l对算法准确率的影响

Fig。2Influence on accuracy of l

l

图3l对算法时间消耗的影响

Fig。3Influence on complexity of l

α

图4平衡因子α对算法准确率的影响

Fig。4Influence on accuracy of α

3。2。3参数λA和λC对推荐结果的影响

概率矩阵联合分解模型有5个参数，分别为λA，λC，λU，λV，λW，在这部分实验中，主要讨论λA和λC的影响，而其他3个参数为了简单起见设置为相同的值，并通过交叉验证（crossvalidation）的

方式获取这3个参数的最优值，即λU=λV=λW=0。05。TagRecUPMF算法中λA决定了资源标签关系矩阵对算法的影响权重，而λC决定了用户标签关系矩阵对算法的影响权重。当这两者同时设为0时，表示算法在进行推荐时，仅考虑用户资源关系矩阵，而当λA或λC设为+

SymboleB@ 时，则意味着仅利用资源标签关系矩阵或者用户标签关系矩阵。实验结果如图5所示，图中显示了在λA和λC的不同取值时的算法准确率。当λA=1，λC=0。6时，TagRecUPMF算法的准确率最高。这表明这两个参数相互约束，而用户标签关系矩阵的影响更显著。这是因为面向用户推荐标签时，资源和标签之间的相似关系受语义影响较大（多义或同义），而用户和标签之间的关系虽然受用户的主观影响，但依然反映了用户对标签的特殊偏好，因此在推荐过程中需要考虑这两种关系的权衡，也应更多地考虑用户对标签的个性化因素。

图5参数λA和λC对算法准确度的影响

Fig。5Influence on accuracy of λAandλC

3。2。4推荐算法的性能比较

该部分实验是将TagRecUPMF算法和目前常见的部分经典算法从准确率和时间消耗两个方面进行比较，选用的参照算法包括基于协同过滤的标签推荐（TagRecCF）、基于Tucker分解的标签推荐、非负矩阵分解标签推荐算法（NMF）、基于三部图张量分解标签推荐算法（TTD）以及PITF算法。

表2是在不同训练数据集规模时各算法的F1值（10次实验结果取平均值）。由表1可以看出，在训练数据集比例较小（<50%）时，TagRecUPMF算法准确度相对其他算法而言均有提升，当比例较大时，TagRecUPMF算法比TTD算法的准确度略低，而相比其他算法依然高出7%～13%，其中TagRecCF算法的准确度受数据稀疏影响最大，准确率最低，实验结果呈现这种现象的原因是Tucker，NMF，PITF算法未考虑用户对资源的评分，影响了准确度，而TTD算法虽然没考虑评分，但它不仅仅考虑实体间的直接关系，还考虑了两两实体因为第三方实体而产生的间接关系，虽然提高了准确性，但其时间损耗高，在实际应用中并不实用。

表3为时间消耗统计情况，其中时间消耗最大的是Tucker算法，其次是TTD算法，而PITF和本文的TagRecUPMF时间消耗最小，PITF算法的时间消耗略低于TagRecUPMF算法，这是由于PITF算法没有考虑评分数据，因此在时间性能上略为占优，但在时间复杂度上，这两者方法依然同为线性级别。因此，比较各算法在准确率和时间消耗指标上的综合情况，本文的TagRecUPMF算法相比其他算法而言表现出了一定的优势。

表2TagRecUPMF算法与其他参照算法的准确率比较

Tab。2Accuracy comparison between TagRecUPMF and other reference algorithms

训练数据集比例/%

F1

TagRecCF

Tucker

NMF

PITF

TTD

TagRecUPMF

90

0。456 3

0。476 9

0。516 9

0。505 9

0。596 7

0。589 6

70

0。359 6

0。456 1

0。491 2

0。472 7

0。571 3

0。565 9

50

0。156 6

0。432 3

0。468 5

0。456 9

0。498 8

0。544 4

30

0。086 9

0。410 1

0。453 6

0。443 2

0。482 3

0。521 1

表3TagRecUPMF算法与其他参照算法的时间消耗比较

Tab。3Time consuming between TagRecUPMF and other reference algorithms

训练数据集比例/%

运行时间/min

TagRecCF

Tucker

NMF

PITF

TTD

TagRecUPMF

90

165

378

243

87

356

88

70

99

201

120

47

183

49

50

65

128

53

27

129

31

30

50

96

34

21

98

22

4总结

在社会标签推荐系统中，由于数据非常稀疏，加上现有的标签推荐算法并未充分利用标签标注系统中的相关信息，因此精度不高，而矩阵、张量分解等技术用一种降维的方法表示稀疏数据，缓解了数据稀疏带来的精度问题。本文基于概率矩阵分解，将用户、标签、资源三方面的潜在特征因子进行联合分解，并将求得的特征向量两两之间的内积进行线性加权并产生推荐。在实验过程中讨论了TagRecUPMF算法中各参数对结果的影响，根据实验结果综合精度和时间损耗指标可以得出，TagRecUPMF算法相比当前流行的算法具有一定的优势。

参考文献

[1]RENDLE S， SCHMIDTTHIEME L。 Pairwise interaction tensor actorization for personalized tag recommendation ＼[C＼]//Proceedings of the 3rd ACM International Conference on Web Search and Data Mining。 New York，USA：ACM，2010：81-90。

[2]JSCHKE R， MARINHO L， HOTHO A， et al。 TagRecommendations in folksonomies＼[J＼]。 Knowledge Discovery in Databases： PKDD，2007，47（2）： 506-514。

[3]SIGURBJRNSSON B， VAN ZWOL R。 Flickr tag recommendation based on collective knowledge＼[C＼] //Proceedings of the 17th International Conference on World Wide Web。 Beijing：ACM， 2008： 327-336。

[4]SEN S， LAM S K， RASHID A M， et al。 Tagging， communities， vocabulary， evolution＼[C＼]//Proceedings of the 2006 20th Anniversary Conference on Computer Supported Cooperative Work。 New York， USA：ACM， 2006： 181-190。

[5]HOTHO A， JSCHKE R， SCHMITZ C， et al。 BibSonomy： A social bookmark and publication sharing system＼[C＼]//Proceedings of the Conceptual Structures Tool Interoperability Workshop at the 14th International Conference on Conceptual Structures。 Aalborg， Denmark， 2006：87-102。

[6]廖志芳，李玲，刘丽敏，等。三部图张量分解标签推荐算法＼[J＼]。计算机学报，2012，35（12）：2625-2632。

LIAO Zhifang， LI Lin， LIU Limin，et al。 A tripartite decomposition of tensor for social tagging ＼[J＼]。Chinese Journal of Computers， 2012，35（12）：2625-2632。（In Chinese）

[7]MA H， YANG H， LYU M R， et al。 Sorec： Social recommend dation using probabilistic matrix factorization ＼[C＼]//Proceedings of the 17th ACM Conference on Information and Knowledge Management。 New York， USA：ACM， 2008： 931-940。

[8]SYMEONIDIS P， NANOPOULOS A， MANOLOPOULOS Y。 TagRecommendations based on tensor dimensionality reduction＼[C＼]//Proceedings of the 2008 ACM Conference on Recommender Systems。 Lausanne， Switzerland：ACM， 2008： 43-50。

[9]LANGSETH H， NIELSEN T D。 A latent model for collaborative filtering＼[J＼]。 International Journal of Approximate Reasoning， 2012， 53（4）： 447-466。

[10]POLAT H， DU W。 SVDbased collaborative filtering with privacy＼[C＼]//Proceedings of the 2005 ACM Symposium on Applied Computing。New York， USA：ACM，2005： 791-795。

[11]MA H， KING I， LYU M R。 Learning to recommend with social trust ensemble＼[C＼]//Proceedings of the 32nd Inter National ACM SIGIR Conference on Research and Development in Information Retrieval。 Boston，USA：ACM，2009： 203-210。

[12]朱郁筱，吕琳媛。推荐系统评价指标综述＼[J＼]。电子科技大学学报，2012，41（2）：163-175。

ZHU Yuxiao， LV Linyuan。 Evaluation metrics for recommender systems＼[J＼]。 Journal of University of Electronic Science and Technology of China， 2012， 41（2）： 163-175。 （In Chinese）