中小学教育信息化评价指标体系构建

杨军

中小学教育信息化评价指标体系构建

杨军

（渤海大学教育与体育学院，辽宁锦州121013）

为给中小学的自身发展和教育管理部门决策提供依据，对中小学教育信息化建设进行综合评价。在综合分析的基础上运用集值迭代法构建评价指标体系，为系统评价提供支持。首先，构建了由6个一级指标和24个二级指标组成的评价指标体系递阶层次模型，并对一级指标进行描述；然后，构建集值迭代法权重计算数学模型，包括基本数学模型和迭代过程与策略；最后，按照求解过程计算指标体系权重。结果表明，集值迭代法计算指标权重算法简单易行，当同级指标数量较多时权重结果更客观真实。

中小学；教育信息化；评价；指标体系；集值统计迭代法

0 引 言

教育信息化是指在教育过程中比较全面地运用以计算机多媒体和网络通信为基础的现代化信息技术，促进教育的全面改革，使之适应于信息化社会对于教育发展的新要求。近年来，我国的中小学教育信息化建设取得了长足发展，促进了素质教育的全面实施、深化了教育改革、提高了教学质量和效率。但中小学教育信息化在发展过程中也存在一些问题，如何加大投入和融合信息资源以及充分发挥设施设备的使用效益等问题，成为阻碍教育信息化可持续发展的瓶颈。对中小学教育信息化的建设情况进行评价，可用于中小学校从纵向发展和横向发展两个维度进行自我评价，从微观上为教育信息化的具体实施提供帮助；也可用于教育管理部分进行校际间或区际间的横向评价，从宏观上为中小学教育信息化建设决策提供依据［1］。指标体系构建是系统评价的基础性工作，笔者通过对中小学教育信息化的发展建设应用情况进行多层次全方位分析，建立一套完整的中小学教育信息化评价指标体系，为中小学和教育主管理部门进行教育信息化评价提供有益指导。

1 评价指标选择

评价指标选择是指运用系统工程的方法，遵循科学性、系统性、综合性、层次性和动态性等原则，对搜集到的数据进行归纳整理（既要运用逻辑推理方法，也要以事实为依据），将主、客观因素相结合，综合选择出评价指标的过程。

1.1 指标体系结构模型

结构是指对事务存在的各个构成要素以及各要素之间的相互关系。指标体系是由若干个相互联系的指标组成的有机体，不是将指标的简单堆积和随意组合，而是按系统性和规律性建立的具有一定结构的指标集合，通常用递阶层次模型表示。递阶层次模型将评价指标体系抽象为由若干个组成对象逐层上、下关联构成，最顶层为目标层，从上往下逐层分解，上、下层组成对象之间是一对多的关联关系［2］。根据文献［3-5］的研究成果并经过笔者的分析与综合，将中小学教育信息化评价指标体系归纳为6个1级指标和24个2级指标，指标体系结构模型如图1所示。

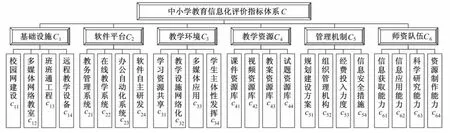
图1 中小学教育信息化评价指标体系结构模型Fig.1 Structuremodel on evaluation index system for educational informatization of primary and secondary schools

1.2 指标描述

对图1中的1级指标简要描述如下。

基础设施。基础设施是教育信息化的物质基础和必要条件，抓好基础设施建设可为信息化发展积蓄能量并增添后劲。基础设施建设又是一项系统性工作，必须科学规划、综合部署才能使其发挥作用。

软件平台。软件平台为教育信息化的应用提供具体功能，使用对象包括教师、学生和教学管理人员等，通常包括教务管理、在线教学、办公自动化等通用系统，还应包括完成个性化教学和学习的自主研发软件。

教学环境。信息化教学环境包括信息化教学活动赖以持续开展的各种因素条件，是将信息技术有效地融合于教学过程中，改变传统的以教师为中心的课堂教学结构，有利于培养学生的创新精神与实践能力。

教学资源。教学资源是为教学有效开展提供的素材等各种可被利用的条件，信息化教学资源主要以资源库的形式存在，为教师和学生提供多种媒体的教学信息，方便教师备课和教学以及学生在线学习。

管理机制。管理机制是指管理系统的结构及其运行机理。教育信息化的管理机制是信息技术有效应用的保障性指标，一方面保障教育信息化的日常运行和正常使用；另一方面保障教育信息化的可持续发展［6］。

师资队伍。教师队伍建设既是教育信息化的重要组成部分，又是推动教育信息化建设的重要力量。因此，建设一支能运用现代信息技术和教育技术进行教育教学的教师队伍是实施教育信息化的基本条件。

2 权重计算数据模型

权重是一个相对概念，表明评价指标在评价指标体系中的相对重要程度，不同的权重取值往往导致不同的评价结果。因此，确定指标权重是构建评价指标体系的重要工作。权重计算的方法很多，包括定量统计法、专家评定法和对偶比较法等。笔者选用的集值迭代法是定量统计法与专家评定法相结合的一种方法。集值迭代法不需要对指标进行很细致的比较，只需每次从指标体系中选出重要的一个或几个指标，然后通过统计计算得到权重值，是一种简单易行、便于实现的方法。

2.1 基本数学模型

数学模型从定性或定量的角度刻画实际问题，并为解决现实问题提供精确的数据或可靠的指导。笔者基于集值迭代法的数学模型构建如下［7-10］。

问题描述：设评价系统C有m个评价指标，构成的评价指标集合为C=｛c1，c2，…，cm｝。聘请评价的专家有n位，评价专家构成的集合为E=｛E1，E2，…，En｝。分别让每位专家在指标集中独立地任意选取自认为重要的s（1≤s＜m）个指标。m个评价指标的权重构成的权重向量集为W=｛w1，w2，…，wm｝。集值迭代法的计算权重求解过程就是根据专家的评价计算权重向量。

第t位专家选取的结果是指标集C的一个子集

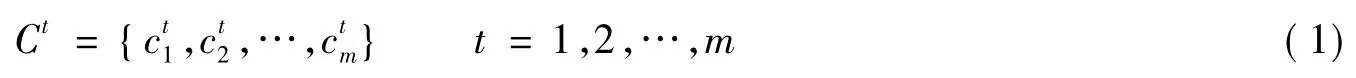
覆盖率记作

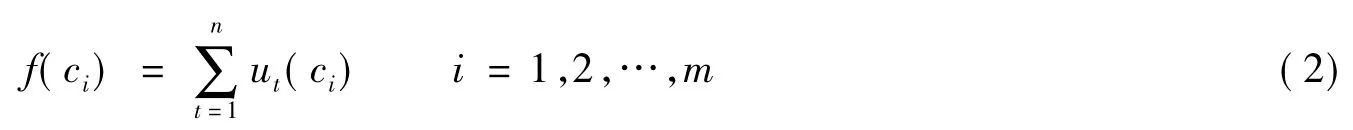
其中

将f（ci）归一化，得到各个指标的权重

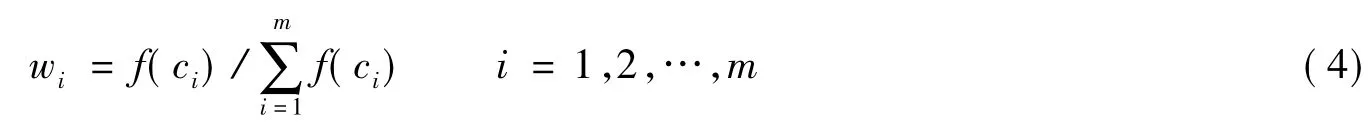
如果某一指标未被选中，则权重系统调整为［11］

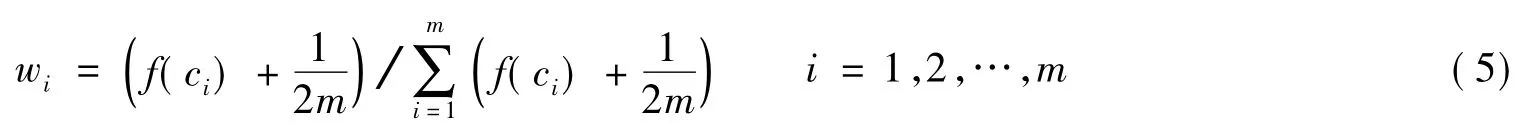
由于专家的专业水平、学识经验等方面不同，因此在所起的作用不同，需要为每位专家赋予不同的权重，这样计算的结果才更客观。n位专家的权重向量为λ=｛λ1，λ2，…，λn｝，则公式（2）改变如下

2.2 迭代策略与过程

为保证结果的客观性，需要选取不同的迭代策略进行多次迭代。迭代策略包括等速迭代和不等速迭代。

1）等速迭代法。选取一个正整数p（1≤p≤m）为初值，每次选取的指标个数按P=｛p，2p，3p，…，sp｝的数量进行，即每次都递增p个，因此称为等速迭代。第t位专家选取指标的过程如下：在指标集合C中第t位专家选取他认为最重要的p个指标，得到第1次选择指标集合Ct，1=｛ct，1，1，ct，1，2，…，ct，1，p｝⊂C构成的子集。其中，Ct，i表示第t位专家的第i次选择的指标集合，ct，i，j表示第t位专家第i次选择的第j个指标；在指标集合C中第t位专家选取他认为最重要的2p个指标，得到第2次选择指标集合Ct，2=｛ct，2，1，ct，2，2，…，ct，2，p｝⊂C构成的子集；…；在指标集合C中第t位专家选取自认为最重要的qp个指标，得到第q次选择指标集合Ct，q=｛ct，q，1，ct，q，2，…，ct，q，p｝⊂C构成的子集。

若存在自然数q，当0≤h≤p时，满足qp+h=m，则第t位专家选择过程结束。

2）不等速迭代法。不等速迭代就是每次迭代不是递增p个元素，而是专家根据自己的判定决定递增多少个元素，每次递增数不同，这样迭代的结构才更符合实际情况，更能表达专家的意见。不等速迭

代又分为加速迭代法和减速迭代法两种。

仍然是选取一个正整数p（1≤p≤m）为初值，每次选取的指标个数按φ（q）p｝的数量进行，第t位专家选取指标的过程如下：第t位专家选取他认为最重要的φ（1）p个指标，得到第1次选择指标集合构成的子集；接着选取他认为最重要的φ（2）p个指标，得到第2次选择指标集合构成的子集；…；以此类推，选取其认为最重要的φ（q）p个指标，得到第q次选择指标集合构成的子集。

3 指标权重计算

笔者权重计算按照加速迭代的方法进行，聘请6位专家E=｛E1，E2，E3，E4，E5，E6｝分别迭代。取p=1，φ（q）=2q（q=0，1，2，…），专家E1对于6个1级指标C=｛C1，C2，C3，C4，C5，C6｝的迭代过程如下。

第1次：φ（0）p=1×1=1 C1

第2次：φ（1）p=2×1=2 C1，C6，C5

第3次：φ（2）p=4×1=4 C1，C6，C5，C3，C2，C4

根据式（3），统计结果如下：C1（3），C2（1），C3（1），C4（1），C5（2），C6（2）。

专家E1对各2级指标的迭代过程以及其他专家对所有指标的迭代过程从略，迭代统计结果见表1的前12行所示。6位专家的权重向量为λ=（0.8，0.9，1.0，1.1，1.3，1.7），对表1的前12行数据分别乘以相应的权重，结果（用Gi（i=1，2，3，4，5，6）表示）如表1的后12行所示。

表1 中小学教育信息化评价指标权重计算迭代数值Tab.1 Iterative numerical on weight calculation for educational informatization of primary and secondary schools

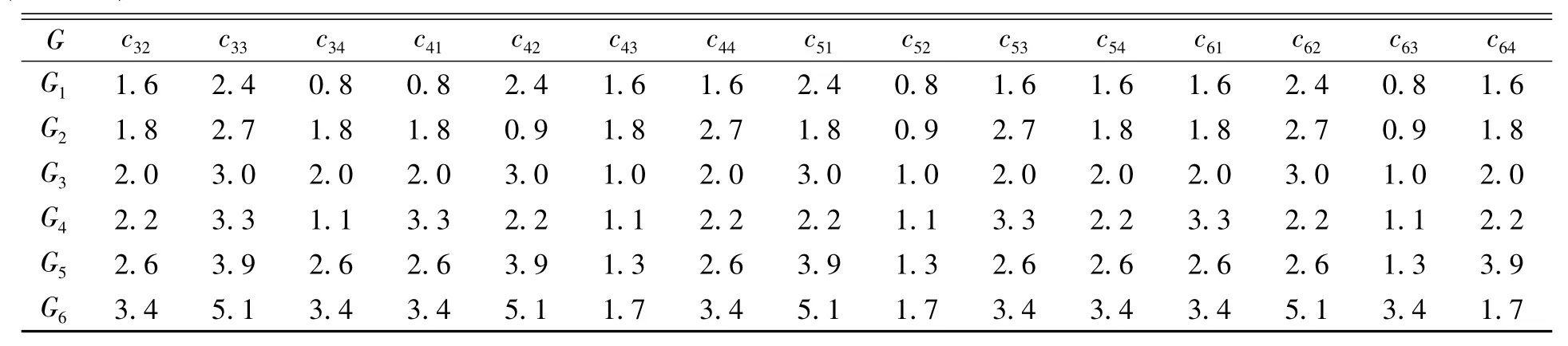
（续表1）

利用式（6）计算1级指标的覆盖率。为了简化数据显示，省略指标数与专家数的乘积（6×6=36），计算过程如下

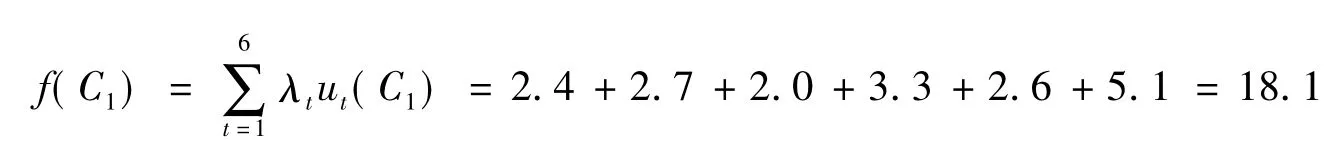
运用同样的方法，各1级指标对应2级指标的权重向量分别为：

基础设施C1=｛c11，c12，c13，c14｝下2级指标的权重向量W1=｛w11，w12，w13，w14｝=｛0.356，0.254，0.195，0.195｝；

软件平台C2=｛c21，c22，c23，c24｝下2级指标的权重向量W2=｛w21，w22，w23，w24｝=｛0.283，0.334，0.155，0.228｝；

教学环境C3=｛c31，c32，c33，c34｝下2级指标的权重向量W3=｛w31，w32，w33，w34｝=｛0.160，0.250，0.375，0.215｝；

教学资源C4=｛c41，c42，c43，c44｝下2级指标的权重向量W4=｛w41，w42，w43，w44｝=｛0.256，0.322，0.156，0.266｝；

管理机制C5=｛c51，c52，c53，c54｝下2级指标的权重向量W5=｛w51，w52，w53，w54｝=｛0.338，0.125，0.287，0.250｝；

师资队伍C6=｛c61，c62，c63，c64｝下2级指标的权重向量W6=｛w61，w62，w63，w64｝=｛0.270，0.331，0.156，0.243｝。

4 结语

中小学教育信息化的广泛应用，对基础教育产生了深刻影响，引起了教育方式的深刻变革。笔者构建的评价指标体系为中小学教育信息化评价奠定了基础，对促进中小学教育信息化发展具有重要意义。研究结论如下：

1）“基础设施、师资队伍”两个1级指标和“校园网建设、多媒体网络教室、规划建设方案、信息获取能力”等2级指标权重较大，进行信息化建设时要重点向这些方面倾斜；

2）集值迭代法计算指标权重算法简单易行，但当指标数量较少时，指标间的权重相差不大，与实际情况不相符，如果笔者的评价指标体系只设置两层，权重计算结果更客观真实。

［1］成江荣，解月光.农村中小学教育信息化绩效评估指标体系的构建［J］.中国电化教育，2011，32（2）：47-52.CHENG Jiangrong，XIE Yueguang.Construction on performance Evaluation Index System of Education Informatization in Rural primary and Middle Schools［J］.China Educational Technology，2011，32（2）：47-52.

［2］李峙，陈朝晖.递阶层次结构对象模型设计及应用［J］.微计算机信息，2009，25（11/1）：4-5. LIZhi，CHEN Zhaohui.Designs and Applications of an Object Module for the Hierarchical Structure［J］.Microcomputer Information，2009，25（11/1）：4-5.

［3］人民教育出版社课程教育研究所.中小学教育信息化的主要任务［EB/OL］.［2014-09-15］.http：//www.pep.com.cn/ xxjs/jszj/jyxxh/201008/t20100827_785316.htm.

［4］Courses and Textbooks Research Institute of people's Education press.Main Task of Education Informatization in primary and Secondary Schools［EB/OL］.［2014-09-15］.http：//www.pep.com.cn/xxjs/jszj/jyxxh/201008/t20100827_785316.htm.

［5］JAMEE KIM，WONGYU LEE.An Analysis of Educational Informatization Level of Students，Teachers，and parents：in Korea［J］.Computers&Education，2011，56（3）：760-768.

［6］FARIDEH HAMIDI，MARYAM MESHKAT，MARYAM REZAEE，et al.Information Technology in Education［J］.procedia Computer Science，2011，3（1）：369-373.

［7］刘朋.上海市浦东新区中小学教育信息化评价的实践探索［J］.教育测量与评价，2010，3（12）：12-15. LIU peng.practice and Exploration on Educational Information Evaluation for Schools of ShanghaiCity pudong New Area［J］. Educational Measurement and Evaluation，2010，3（12）：12-15.

［8］百度文库.集值统计迭代法在指标赋权中的应用［EB/OL］.［2014-09-15］.http：//wenku.baidu.com/link？url= pJICW12r1Gc111KVVi61i5gieX3c8I3UsAhN1SDnck9qu2gCWcj，2014-9-15. Baidu Library.Application on Set-valued Iteration in Index Weight［EB/OL］.［2014-09-15］.http：//wenku.baidu.com/ link？url=pJICW12r1Gc111KVVi61i5gieX3c8I3UsAhN1SDnck9qu2gCWcj，2014-9-15.

［9］吴雪靖，刘凯.基于集值统计理论的供应链风险评价研究［J］.物流技术，2009，28（10）：100-102. WU Xuejing，LIU Kai.Supply Chain Risk Evaluation Based on Set-Valued Statistics［J］.Logistic Technology，2009，28（10）：100-102.

［10］MAREK CEZARY ZDUN.On Set-Valued Iteration Groups Generated by Commuting Functions［J］.Journal of Mathematical Analysis and Applications，2013，398（2）：638-648.

［11］GRA.ZYNAŁYDZI~NSKA.On Lower Semicontinuity of Some Set-Valued Iteration Semigroups［J］.Nonlinear Analysis：Theory，Methods&Applications，2009，71（11）：5644-5654.

（责任编辑：刘东亮）

Construction of Evaluation Index System for Educational Informatization of primary and Secondary Schools

YANG Jun

（School of Education and Sports，Bohai University，Jinzhou 121013，China）

Comprehensive evaluation on construction of educational informatization in primary and secondary schools provides a basis for the development of primary and secondary schools themselves and the decision of educationalmanagement.This article uses set-valued iteration to construct the evaluation index system to support system evaluation on the basis of the comprehensive analysis.First，construct the hierarchical model of evaluation index system which consisted of6 primary indicators and 24 secondary indicators，and provide a brief description of the primary indicators.Then，set up weight calculation mathematical model about set-valued iteration，including the two aspects of basic mathematics model and iterative process with strategy.Finally，according to the solving process to calculate the weight of index system.The results show that themethod using the set-valued iterative to calculate index weight algorithm is simple，but the results in weight aremore objective and realwhen the number of the same index aremore.

primary and secondary schools；educational informatization；evaluation；index system；setvalued iteration

Tp39；N945.1；G434

A

1671-5896（2015）03-0344-06

2014-10-09

2014年辽宁省普通高等教育本科教学改革研究基金资助项目（UpRp20140249）；辽宁省教育科学“十二五”规划2013年基金资助项目（JG13CB030）；2013年渤海大学教学改革研究基金资助项目（JG13YB004）

杨军（1969— ），女，辽宁锦州人，渤海大学副教授，硕士生导师，主要从事教育信息化及小学教育研究，（Tel）86-13941668878（E-mail）yangjun690213@163com。