惯性/北斗组合导航系统的鲁棒H∞滤波

李艳辉，杨 琦

惯性/北斗组合导航系统的鲁棒H∞滤波

李艳辉，杨 琦

（东北石油大学电气信息工程学院，黑龙江大庆163318）

为提高惯性/北斗组合导航系统的精度，将鲁棒H∞滤波算法应用于惯性/北斗组合导航系统中，该算法可克服模型的不确定性对滤波精度的影响，并将滤波器的设计问题转化为线性矩阵不等式约束的凸优化问题。仿真试验最终表明，鲁棒H∞滤波算法应用于组合导航系统是有效的。

鲁棒H∞滤波；惯性/北斗组合导航；线性矩阵不等式；凸优化

0 引言

惯性/北斗组合导航系统因其自主性强、隐蔽性好、可靠性高等优点，近年来得到广泛关注，是目前我国导航领域的一个重要研究方向［1-3］。采用传统的卡尔曼滤波算法处理组合导航系统的滤波问题时，很难达到期望的精度及可靠性［4］。鲁棒滤波算法可提高系统对模型不确定性的鲁棒性，应用于组合导航系统中可改善系统的滤波精度［5］。

鲁棒滤波是在不确定性允许范围内估计系统状态，使系统稳定并满足一定的性能指标约束。文献［6］通过鲁棒H∞滤波的黎卡提迭代算法，较好地估计了观测噪声的统计特性不确定的惯性/雷达组合导航系统。文献［7］研究系统模型为非线性的多卫星组合导航系统，采用鲁棒滤波算法有效估计系统状态。文献［8］针对噪声的统计特性未知的导航系统，应用闭环鲁棒H∞滤波算法，在保证系统鲁棒性的同时提高了滤波精度。

笔者针对导航系统动态模型不确定而外部噪声干扰的统计特性也不确切已知的问题，研究了基于组合导航系统的鲁棒H_______________________________∞滤波算法，采用线性矩阵不等式技术设计和求解滤波器［9］，实现对该系统的状态估计。该算法不局限于数值仿真，易于计算机实现，可真正应用于运载体实际运动的离线仿真，修正导航参数。最后通过仿真试验，验证该滤波算法是可行有效的。

1 组合导航系统建模及滤波

笔者采用惯性/北斗位置、速度组合模式，该模式是以惯导系统为主，辅以北斗卫星提供的位置、速度信息，共同提供导航数据；状态变量选取为导航系统的参数误差，量测变量选取为惯导系统与北斗接收机的量测信息差值。选取以地球固联系“东北天”系为参考坐标系（见图1）。系统模型形式如下

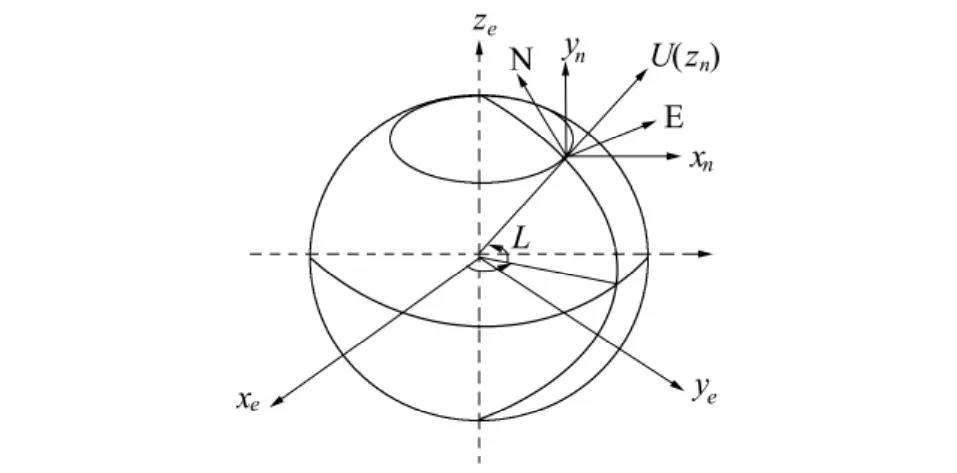
图1 运载体与参考系的关系Fig.1 The relationship between machine and the reference frame

为导航系统在东、北、天向的重力加速度分量，l（t）为当前时刻纬度值，R为地球半径

满足BDT=0，εb，εr，▽b，▽r为陀螺和加速度计的随机漂移与常值漂移，而实际系统通常直接对状态量进行估计，故L=I。

式（1）所表示的系统模型是非线性的，导航解算较困难，但由于有限时间内运载体在平衡点附近变化缓慢，非线性程度较小，因此近似线性化处理系统模型为

其中A、C为适当维数的定常矩阵，不确定性系数矩阵ΔA（t）、ΔC（t）满足为已知适当维数的定常矩阵。

实际组合导航系统的动态模型复杂且运载体空间运动变化具有不确定性，外部噪声干扰的统计特性也不完全已知，针对上述模型的特点，构建如下形式的鲁棒H∞滤波器

笔者针对组合导航系统（2），设计了鲁棒H∞滤波器，使滤波误差系统（4）渐近稳定且对于任意的，满足H∞性能指标约束。

在求取滤波器存在的充分条件前，首先给出后续证明过程中需要用到的以下两个引理［10］。

引理1 设α、β为适当维数向量或矩阵，对适当维数矩阵M，F，N和常量ε＞0（其中FTF≤I），有

引理2 考虑系统（2），滤波误差系统（4）渐近稳定且‖~z（t）‖2≤γ‖~w（t）‖2（γ＞0）的充分条件是存在正定矩阵P=PT满足

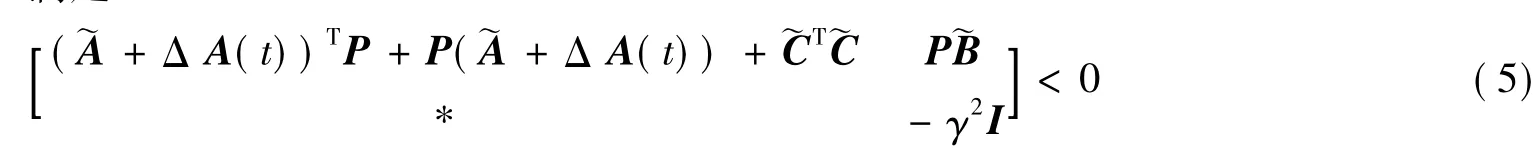
2 组合导航系统鲁棒H∞滤波器设计

利用线性矩阵不等式技术，求解鲁棒H∞滤波器存在的充分条件，并将其转化为凸优化问题求解。

定理1 对于系统（2），鲁棒 H∞滤波器存在的充分条件为矩阵及标量ε＞0满足

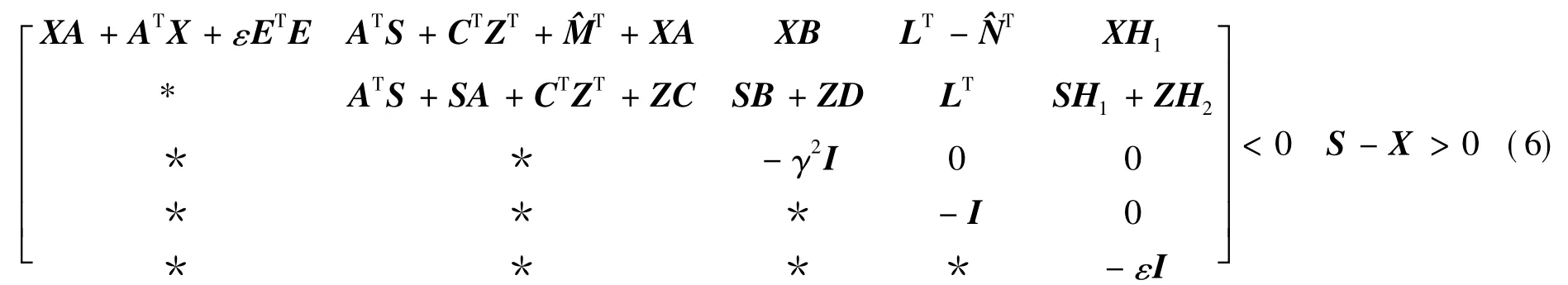
证明 根据引理1，式（5）改写为

对式（7）进行矩阵变换，将P及P-1分块，即，取，，则，令），式（7）左乘ΩT和右乘Ω，有

推论1 对于实际组合导航系统，可通过求解如下形式的凸优化问题获得系统的γ次优H∞滤波器

且鲁棒H∞滤波器参数可通过定理1求得。

3 系统仿真研究

仿真实验采取半物理仿真形式，通过跑车试验采集数据并离线仿真，其中惯导系统选用国内某公司生产的光纤惯导，接收机选用无源北斗二代接收机，且假设惯导数据与北斗数据完全同步，载体在水平面上运动。各传感器在组合导航系统中的误差如表1所示，仿真初始条件如表2所示。

表1 各传感器误差量Tab.1 Errors of each sensor

表2 仿真初始条件Tab.2 Initial conditions of the simulation

试验分别在平稳路段和非平稳路段两种情况下进行，为便于对比分析，选用卡尔曼滤波与鲁棒H∞滤波两种方法对系统进行处理，图2～图9所示为系统仿真曲线。

在平稳路段，图2、图3中两种滤波方法均可实时跟踪北斗卫星信号，估计系统速度，同样图4、图5中两种滤波方法均可有效跟踪载体的经纬度变化；在非平稳路段，受系统运动状态变化影响，图6、图7中两种滤波算法虽能实时跟踪系统的速度变化但卡尔曼滤波精度下降，与北斗卫星实测值偏差较大，而在图8、图9中，卡尔曼滤波输出曲线产生较大跳动，而鲁棒H∞滤波曲线变化平稳。

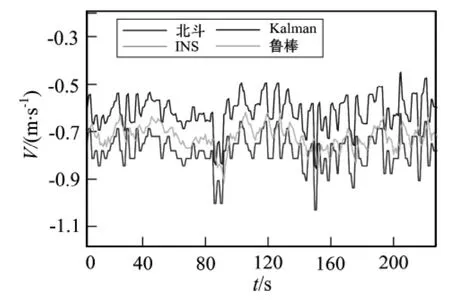
图2 平稳路段东向速度Fig.2 The east velocity of the flat

图3 平稳路段北向速度Fig.3 The north velocity of the flat

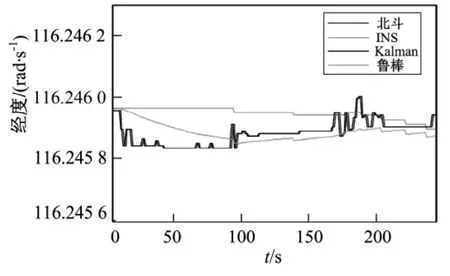
图4 平稳路段经度Fig.4 The longitude of the flat

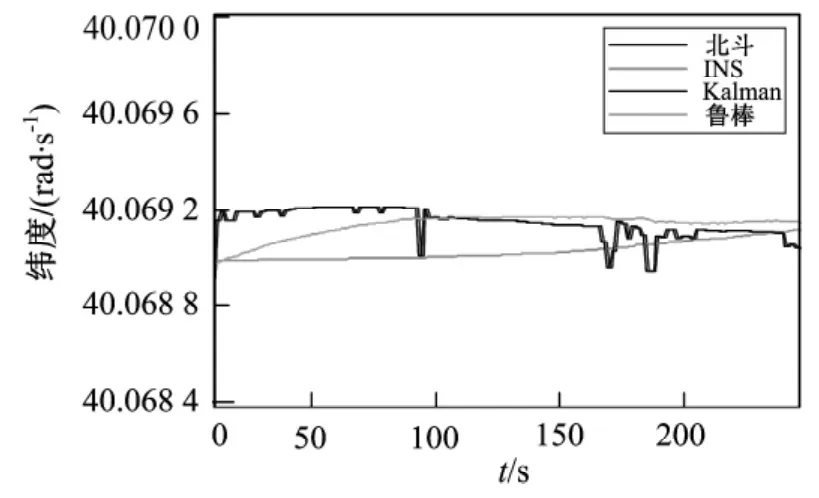
图5 平稳路段纬度Fig.5 The latitude of the flat

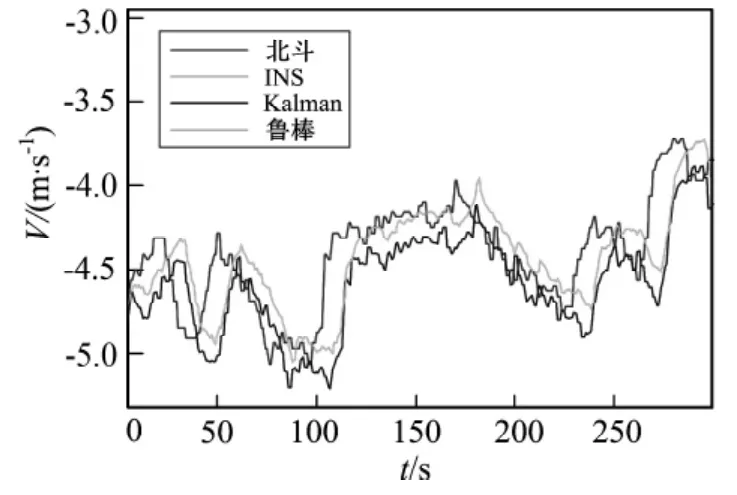
图6 非平稳路段东向速度Fig.6 The east velocity of the rugged road

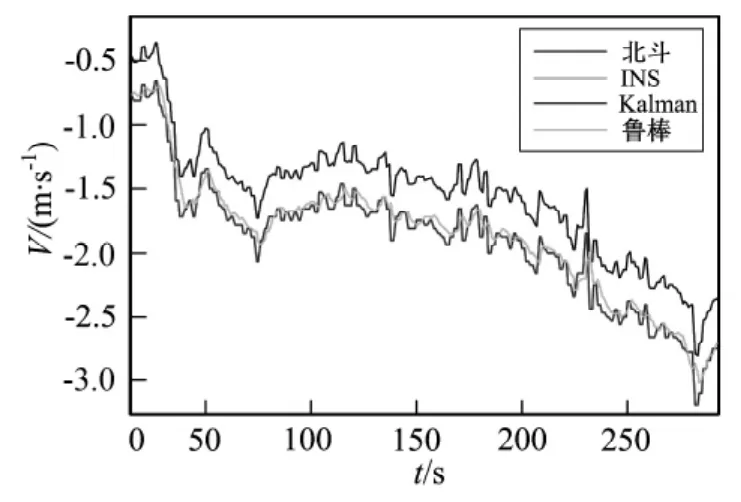
图7 非平稳路段北向速度Fig.7 The north velocity of the rugged road

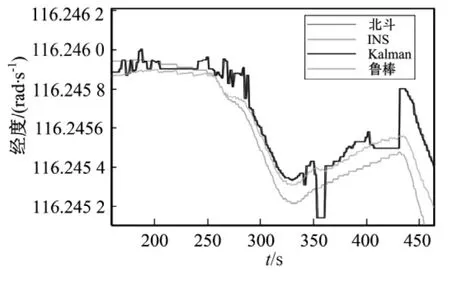
图8 非平稳路段经度Fig.8 The longitude of the rugged road

图9 非平稳路段纬度Fig.9 The latitude of the rugged road

通过对比分析曲线可以得出，当外界干扰相对较小，两种滤波算法都能有效估计系统状态，修正导航参数；当系统受外界干扰较大时，卡尔曼滤波估计值有明显跳变，精度下降。鲁棒H∞滤波不易受机体自身及外界干扰的影响，可保证滤波精度及可靠性，改善系统的观测性。

4 结语

笔者将鲁棒H∞滤波思想应用于系统模型不确定的惯导/北斗组合导航，将滤波器的设计问题转化为线性矩阵不等式的求解问题，为实际导航系统提供了一种更为有效的状态估计方法。最后通过仿真试验，验证鲁棒H∞滤波具有更好的环境适应性及更高的精度和可靠性。

［1］TAZARTESD A.Inertial Navigation from Gimbaled p latforms to Strapdown Sensors［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（3）：2292-2299.

［2］REN H，KAZANZIDES p.Investigation of Attitude Tracking Using an Integrated Inertial and Magnetic Navigation System for Hand-Held Surgical Instruments［J］.IEEE/ASME Transactions on Mechatronics，2012，17（2）：210-217.

［3］蒋庆仙，田育民，孙葵.北斗/INS组合导航关键技术分析［J］.全球定位系统，2010，35（6）：56-60. JIANG Qingxian，TIAN Yumin，SUN Kui.The Crucial Technologies in INS/BD Integrated Navigation System［J］.GNSS World of China，2010，35（6）：56-60.

［4］WARD B D，JANIK J，MAZAHERIY，et al.Adaptive Kalman Filtering for Real-Time Mapping of the Visual Field［J］. NeuroImage，2012，59（4）：3533-3547.

［5］UGRINOVSKIIV.Distributed Robust Filtering with H∞Consensus of Estimates［J］.Automatica，2011，47（1）：1-13.

［6］GAO Shesheng，ZHONG Yongmin，LIWei.Robust Adaptive Filtering Method for SINS/SAR Integrated Navigation System［J］.Aerospace Science and Technology，2011，15（6）：425-430.

［7］XIONG K，LIU L，LIU YW.Nonlinear Robust Filter Design for Satellite Attitude Determination［J］.IETControl Theory and Applications，2010，4（7）：1222-1234.

［8］康国华，刘建业，刘瑞华，等.闭环H∞滤波在无源北斗/SINS导航系统中的实现［J］.控制与决策，2007，22（5）：566-568. KANG Guohua，LIU Jianye，LIU Ruihua，et al.Realization of Closed-Cycle H∞Filtering in passive BD/SINS Navigation System［J］.Control and Decision，2007，22（5）：566-568.

［9］KARIMIH R，ZApATEIRO M，LUO N.A Linear Matrix Inequality Approach to Robust Fault Detection Filter Design of Linear Systems with Mixed Time-Varying Delays and Nonlinear perturbations［J］.Journal of the Franklin Institute，2010，347（6）：957-973.

［10］LIHuaizhong，FU Minyue.A Linear Matrix Inequality Approach to Robust H∞Filtering［J］.Signal processing，IEEE Transactions on，1997，45（9）：2338-2350.

（责任编辑：刘东亮）

Robust H∞Filtering on INS/BD Integrated Navigation System

LIYanhui，YANG Qi

（College of Electrical and Information Engineering，Northeast petroleum University，Daqing 163318，China）

INS/BD constitutes an integrated navigation system with high precision and complementary advantages，but the usual Kalman filtering can notobtain a satisfying precision.So the robust H∞filtering is used for the INS/BD integrated navigation system，overcoming the precision impact caused by themodel uncertainty，and converting the problem of filter designing into a convex optimization problem subject to LMI（Linear Matrix Inequality）constraints.Simulation experiments show this algorithm can be used for integrated navigation system effectively.

robust H∞filtering；inertial navigation system（INS）/BD integrated navigation；linear matrix inequality（LMI）；convex optimization

Tp273；V249.32

A

1671-5896（2015）03-0261-06

2014-07-18

黑龙江省博士后科研启动基金资助项目（LBH-Q13177）；黑龙江省自然科学基金资助项目（F201403）

李艳辉（1970— ），女，辽宁法库人，东北石油大学教授，博士生导师，主要从事鲁棒控制、滤波和智能控制研究，（Tel）86-459-6504797（E-mail）LY_hui@hotmail.com，Li_yanhui2006@aliyun.com。