图的两类重复点集与图的几类矩阵的特征值重数
2015-11-30杜志斌
杜志斌
(肇庆学院 数学与统计学院,广东 肇庆 526061)
1 引言
本文所考虑的图皆为无向简单图。作为数与形相互结合的一个典范,图与矩阵具有紧密的联系。给定一个图,可定义出一些相应的矩阵,如邻接矩阵、Laplacian矩阵、无符号Laplacian矩阵、正规化Laplacian矩阵、距离矩阵等。
图谱理论主要运用线性代数方法来研究图的各种性质[1]。在图谱理论中,研究的核心内容是基于图所导出的各类矩阵的特征值,由这些特征值所组成的多重集称为图的谱。
很多情况下,图的特征值不是单根。比方说,n个点的完全二部图的邻接矩阵具有 2n-重特征值0,n个点的完全图的Laplacian矩阵具有1n-重特征值n。因此,为了更好地了解图的各类谱,我们有必要研究图的各类矩阵的特征值重数。
随着改革开放的进一步深入,到20世纪80年代后期,人们的生活水平逐步有了好转,“楼上楼下,电灯电话”成了很多人向往的现代化生活标志。这时候电话已经慢慢普及到了一些富裕的城市家庭,什么初装费,选号费啊,装一部电话,没有数千元根本装不起。电话在那个时代还是“紧俏商品”……直到电话进入普通百姓家庭,打电话才方便了。同时“大哥大”兴起,拥有“大哥大”就是身份和富有的象征。一部“大哥大”一两万元,现在想起来,真有点滑稽。
众所周知,局部子图的结构对图的各种性质有着重要的影响[2]。本文将考虑当局部子图为空图或者完全图时,其对图的几类矩阵的特征值重数的影响。为此,我们首先定义两类局部子图,其定义可见文献[3]。
设V为图G的点集的一个非空子集,记G[V]为由G的点子集V所导出的子图。对于图G中的点v,记Γ(v)为由点v的所有邻点所组成的集合,特别地,称Γ(v)为点v的邻集,而称Γ(v)∪{v}为点v的闭邻集。
刘真表示,掺混肥以其受环保影响小、配方调整快等特点,产量及需求量或有一定程度的增加。与此同时,刘真也表示,终端经销商自行配制掺混肥料并不具有优势,前期的设备投入和并无成本优势的原材料采购,使其生产成本高且价格优势不明显,目前多以为农户“量身定做”进行营销,基层经销商生产掺混肥还会面对政策及环保等压力,转型需谨慎。
定义1[3]设V为图G的点集的一个非空真子集。若G[V]为空图,且V中的点具有相同的邻集,则称V为图G的一个重复点集(duplicate vertices)。
定义2[3]设V为图G的点集的一个非空真子集。若G[V]为完全图,且V中的点具有相同的闭邻集,则称V为图G的一个共同重复点集(co-duplicate vertices)。
下面,我们给出一个例子来阐明图的(共同)重复点集。设图G如图1所示,则可观察到{1,2,3}与{4,5}为G的重复点集,而{6,7,8}为G的一个共同重复点集。
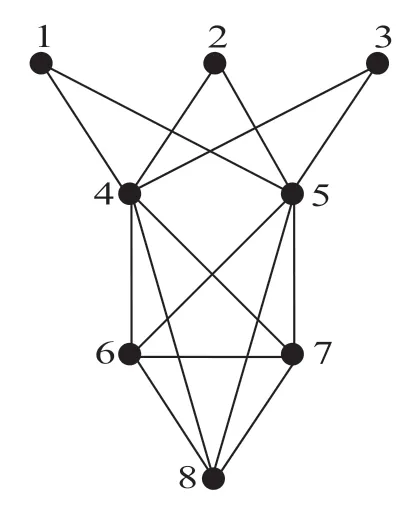
图1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个共同重复点集,也就是说,G[V]是完全图。于是,图G的无符号Laplacian矩阵G(S)结构如下:
在本文中,我们将研究图的(共同)重复点集与图的几类矩阵的特征值重数的联系。
结论可证。
2 预备知识与引理
对于任意实对称阵A,若l是A的一个特征值,则记mA(l)为l的(代数)重数。此外,若l不是A的特征值,则习惯上记作mA(l)=0。
记In为n阶单位矩阵。
矩阵对角化是高等代数中的一个重要内容。特别地,若n阶矩阵A可对角化,则对于任意常数l,总有
秩(A-λIn)=n-mA(λ) (1)
参见[4]。
在确定评估指标后,采用专家打分法对评估指标之间的重要程度进行比较量化。一般的,将比较结果分为5个等级:相同、稍强、较强、很强和绝对强,并且用1~9来表示。通过专家打分对评估指标的重要性进行判定,构造一级评估指标的判断矩阵,如表2。
由于由图所导出的大部分矩阵皆为实对称阵,从而它们可对角化。于是,我们可运用矩阵对角化的知识来研究图所导出的矩阵。
下面,我们利用式子(1)来给出一个关于特征值重数的下界。
引理1:设

为一个n阶实对称阵,其中M为k×k方阵,X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。若分块矩阵(M-λIkX)的每一行具有相同的元素,则
mA(λ)≥k-1
证明:首先,既然A为n阶实对称阵,从而A可对角化。现由(1)可知
秩(A-λIn)=n-mA(λ) (2)
显然

此外,又因为(M-λIkX)的每一行具有相同的元素,也就是说,A-λIn的头k行具有相同的元素,从而有
秩(A-λIn)≤ n-(k-1) (3)
结合(2)与(3),我们有
mA(λ)≥k-1
小丽带男友回家,正赶上老爸喝醉酒回来。只见老爸往沙发上一躺,喊:“闺女,电视又卡了!”小丽走过去,一拍电视机上的鱼缸,里面的鱼四下乱窜。
3 图的(共同)重复点集与图的几类矩阵的特征值重数
下面,我们将研究图的(共同)重复点集与图的几类矩阵的特征值重数之间的联系,其中包括图的邻接矩阵、Laplacian矩阵、无符号Laplacian矩阵、正规化Laplacian矩阵、距离矩阵。
3.1 图的邻接矩阵的特征值重数
图G的邻接矩阵G(A)定义为[1]
(5)单体浓度在m(AMPS)∶m(AA)∶m(AM)为6∶4∶2,水浴温度65℃,引发剂加量0.2%,pH值为6条件下合成缓凝剂,并配置水泥浆(配方A)进行性能评价,实验数据显示最佳的合成单体浓度为30%(表5)。

本小节将研究图的重复点集与图的邻接矩阵的特征值重数之间的联系。
记On为n阶零矩阵。
定理2:若V为图G的一个共同重复点集,则
结论可证。
mA(G)(0)≥|V|-1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个重复点集,也就是说,G[V]是空图。于是,图G的邻接矩阵G(A)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
总之,运用多媒体辅助语文教学,可以说是有利有弊,关键在于教师的把握,在于教师的思想态度。用好多媒体可以促进教学,提高教学效果,既有利于师,也有利于生;如果使用不当多媒体,可能会导致教学效果差,学生反感,教师尴尬,先进的设备变成害生的毒药。
又因为V是图G的一个重复点集,也就是说,V中的点具有相同的邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(Ok-0IkX)=(OkX)
的每一行具有相同的元素。
现利用引理1,可得
mA(G)(0)≥k-1
定理1:若V为图G的一个重复点集,则
随后,西安高新控股于12月3日当天召开临时董事会,会议召开前依法通知了全体董事。会议应到董事5名,实到董事4名,1名董事请假。出席会议的 4 名董事经过表决一致通过了如下决议:
诚龙先生是惯打野枪的,如匕首投枪,刺贪刺虐入木三分。为清官树碑,为贪官画像,几乎篇篇不离讽刺与讽喻,时时不忘警醒与警示。作者之用心,可谓良苦。
mA(G)(-1)≥|V|-1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个共同重复点集,也就是说,G[V]是完全图。于是,图G的邻接矩阵G(A)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
泛舟静静流淌的江水中,欣赏两岸错落有致而鳞次栉比的吊脚楼,人们心里都会自然产生出莫名的感动——这是人类与大自然和谐共处的佳作,而时光则让它的内涵变得更加丰富。在这里,你忘记了时间匆匆流逝,忘却了思考过后的伤口,身心极其愉悦。
又因为V是图G的一个共同重复点集,也就是说,V中的点具有相同的闭邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(Jk-Ik+IkX)=(JkX)
的每一行具有相同的元素。
通过捕获的“肉鸡”进行设备类型分析,以Windows、Linux和IoT设备作为分类范围,其中IoT设备类型的肉鸡最多,占比61.37%;其次是Linux设备类型的肉鸡,占比20.85%,Windows设备类型肉鸡仅占比17.78%。
现利用引理1,可得
mA(G)(-1)≥k-1
结论可证。
3.2 图的Laplacian矩阵的特征值重数
记di为点i在图G中的度数。
图G的Laplacian矩阵 L(G)定义为[5]

本小节将研究图的重复点集与图的Laplacian矩阵的特征值重数之间的联系。
设V为图G的一个重复点集(共同重复点集),既然V中的点具有相同的邻集(闭邻集),从而V中每个点的度数是相同的。
定理3:若V为图G的一个重复点集,则
mL(G)(d)≥|V|-1
其中d为V中每个点的度数。
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V为图G的一个重复点集,也就是说,G[V]为空图。于是,图G的Laplacian矩阵G(L)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
在考场上有限的时间内,如何写出高质量的作文呢?笔者根据多年对中考作文的评阅及平时作文教学的经验,有以下几点感悟。
又因为V是图G的一个重复点集,也就是说,V中的点具有相同的邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(dIk-dIkX)=(OkX)
的每一行具有相同的元素。
现利用引理1,可得
mL(G)(d)≥ k-1
结论可证。
定理4:若V为图G的一个共同重复点集,则
mL(G)(d+1)≥|V|-1
其中d为V中每个点的度数。
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个共同重复点集,也就是说,G[V]是完全图。于是,图G的Laplacian矩阵G(L)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个共同重复点集,也就是说,V中的点具有相同的闭邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
((d +1)Ik-Jk-(d+1)IkX)=(-JkX)
的每一行具有相同的元素。
现利用引理1,可得
再次,网络传播中的自由性、开放性与狂欢要求的客观环境相吻合。狂欢生活是在“广场”上进行的。“广场”不仅是一个具体的场所,而且是大众性、民间性舞台的隐喻。网络传播的自由与开放的属性体现在每个网民自由地进行信息选择与交流,这使得网络传播与以往的传统媒体不同,具有强烈的民间色彩。这种民间色彩满足了狂欢的大众性和民间化特征。
记Jn为一个n阶方阵,其中每个元素皆为1。
mL(G)(d+1)≥k-1
结论可证。
教学实验室主要面向本科生,用于本科实验教学。学生通过实验课对所学课程进行感性认识和动手能力培训,该类实验室的特点是量大面广,人员流动性大。随着各学院组建集中的本科实验教学中心,形成了教辅人员准备实验、教师讲授实验、学生操作实验的格局,这种“管教学”分立的方式,优点在于分工明确,不足是三者之间的交流有时脱节,出现管理空档。同时学生实验课门数多,每门课的课时紧张,因此安全环保教育往往被忽视,也未施行准入制度,易出现操作不当引起的安全隐患、乱丢乱倒有毒有害物质。
3.3 图的无符号Laplacian矩阵的特征值重数
图G的无符号Laplacian矩阵G(S)定义为[3]
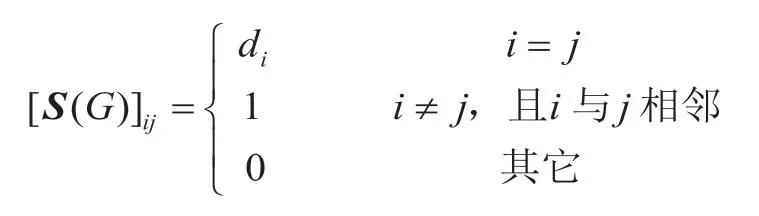
本小节将研究图的重复点集与图的无符号Laplacian矩阵的特征值重数之间的联系。
定理5:若V为图G的一个重复点集,则
mS(G)(d)≥|V|-1
其中d为V中每个点的度数。
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个重复点集,也就是说,G[V]是空图。于是,图G的无符号Laplacian矩阵G(S)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个重复点集,也就是说,V中的点具有相同的邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(dIk-dIkX)=(OkX)
的每一行具有相同的元素。
现利用引理1,可得
mS(G)(d)≥ k-1
结论可证。
定理6:若V为图G的一个共同重复点集,则
mS(G)(d-1)≥|V|-1
其中d为V中每个点的度数。
下面我们不妨假设每个(共同)重复点集V都至少包含两个点,即||2V³ 。
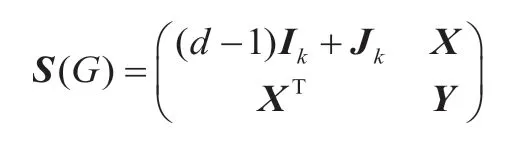
其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个共同重复点集,也就是说,V中的点具有相同的闭邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
((d-1)Ik+Jk-(d-1)IkX)=(JkX)
的每一行具有相同的元素。
现利用引理1,可得
mS(G)(d-1)≥k-1
结论可证。
3.4 图的正规化Laplacian矩阵的特征值重数
图G的正规化Laplacian矩阵G(ℓ)定义为[6]
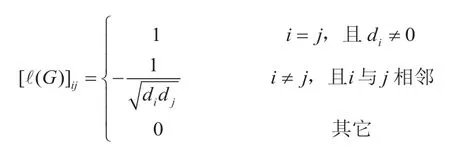
本小节将研究图的重复点集与图的正规化Laplacian矩阵的特征值重数之间的联系。
定理7:若V为图G的一个重复点集,且V中的点不是图G的孤立点,则
mℓ(G)(1)≥|V|-1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个重复点集,也就是说,G[V]是空图。于是,图G的正规化Laplacian矩阵G(ℓ)结构如下:

其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个重复点集,也就是说,V中的点具有相同的邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(Ik-IkX)=(OkX)
的每一行具有相同的元素。
现利用引理1,可得
mℓ(G)(1)≥k-1
结论可证。
定理8:若V为图G的一个共同重复点集,且V中的点不是图G的孤立点,则
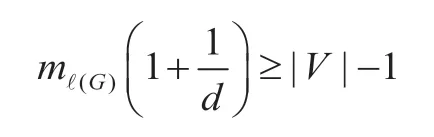
其中d为V中每个点的度数。
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个(共同)重复点集,也就是说,G[V]是完全图。于是,图G的正规化Laplacian矩阵G(ℓ)结构如下:
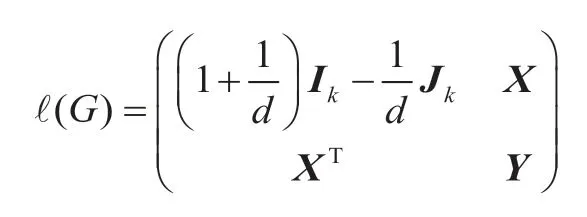
其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个共同重复点集,也就是说,V中的点具有相同的闭邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
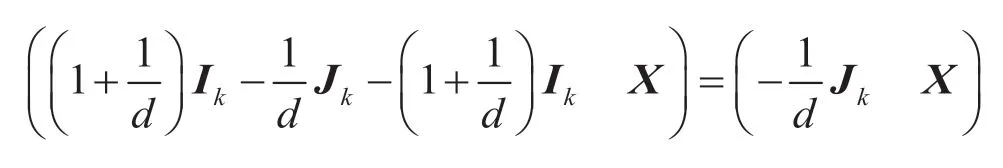
的每一行具有相同的元素。
现利用引理1,可得

结论可证。
3.5 图的距离矩阵的特征值重数
图G的距离矩阵记作G(D),其第i行第j列元素为点i与点j在图G中的距离[7]。
本小节将研究图的重复点集对图的距离矩阵的特征值重数的影响。
定理9:若V为连通图G的一个重复点集,则
mD(G)(-2)≥|V|-1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个重复点集,也就是说,G[V]是空图,且V中的点具有相同的邻集。于是,图G的距离矩阵G(D)结构如下:
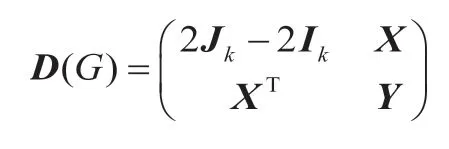
其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V中的点具有相同的邻集,所以分块矩阵X的每一行具有相同的元素。进一步,的每一行具有相同的元素。现利用引理1,可得
(2Jk-2Ik+2IkX)=(2JkX)
mD(G)(-2)≥k-1
结论可证。
定理10:若V为连通图G的一个共同重复点集,则
mD(G)(-1)≥|V|-1
证明:记|V|=k,且不妨假设图G具有n个点,V中的点是图G的头k个点。既然V是图G的一个共同重复点集,也就是说,G[V]是完全图。于是,图G的距离矩阵G(D)结构如下:
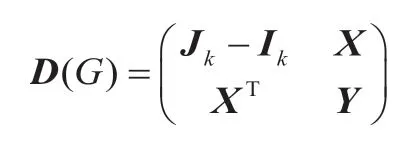
其中X为k×(n-k)矩阵,Y为(n-k)×(n-k)方阵。
又因为V是图G的一个共同重复点集,也就是说,V中的点具有相同的闭邻集,所以分块矩阵X的每一行具有相同的元素。进一步,
(Jk- Ik+IkX)=(JkX)
的每一行具有相同的元素。
现利用引理1,可得
mD(G)(-1)≥k-1
结论可证。
4.例子
现在我们通过图1所示的图来说明定理1-10的下界都是可达的。
设图G如图1所示,注意到{1,2,3}与{4,5}为G的重复点集,而{6,7,8}为G的一个共同重复点集。现利用Mathematica,可算得:
(1)邻接矩阵:mA(G)(0)=3,mA(G)(-1)=2;
(2)Laplacian矩阵:mL(G)(2)=3,mL(G)(6)=1,mL(G)(5)=2;
(3)无符号Laplacian矩阵:mS(G)(2)=2,mS(G)(6)=1,mS(G)(3)=2;
(5)距离矩阵:mD(G)(-2)=3,mD(G)(-1)=2。
这表明:定理1-10中的下界是可达的。
[1]CVETKOVIć D,DOOB M,SACHS H.Spectra of Graphs-Theory and Application[M].New York:Academic Press,1980.
[2]BONDY J A,MURTY U S R.Graph Theory with Applications[M].New York:American Elsevier,1976.
[3]CVETKOVIć D,ROWLINSON P,SIMIć SK.Eigenvalue bounds for the signless Laplacian[J].Publ.Inst.Math.(Beograd),2007,81:11-27.
[4]张和瑞,郝鈵新.高等代数[M].第5版北京:高等教育出版社,2007.
[5]GRONE R,MERRIS R.The Laplacian spectrum of agraph II[J].SIAM J.Discrete Math.,1994,7:221-229.
[6]CHUNG F R K.Spectral Graph Theory[M].Providence:American Math.Soc.,1997.
[7]MERRIS R.The distance spectrum of a tree[J].J.Graph Theory,1990,14:365-369.
