异形管材分流模挤压焊合过程金属流变及模具受力的模拟分析

黄东男，李有来，左壮壮，马 玉

(内蒙古工业大学材料科学与工程学院，呼和浩特 010051)

分流模挤压是铝合金空心型材的主要加工方式，焊合过程是连接分流与成形过程的纽带，分流模模腔内金属焊合流变特征是准确判断挤压成形过程金属流变均匀性、焊缝形状与位置、合理的模具结构设计的判据，也是影响挤压产品质量和生产效率的关键因素，成为近年来金属挤压领域备受关注的研究重点之一［1-2］.

分流模挤压成形时，金属几乎在密闭模具内流动，采用物理模拟方法很难获得金属流动变形行为，有限元数值模拟方法最为可行.已采用有限元法获得了圆管、方管、冷凝器、口琴管挤压时的金属流动行为，死区分布、挤压力变化、温度场、模具受力及焊合质量等信息［3-8］.但目前该方法只能针对建模时可将焊合面设置为刚性对称面，然后采用1/2或1/4的几何模型计算.当焊合面无法设置为刚性对称面时，计算时相互接触的焊合面的网格单元将产生穿透，导致计算自动终止，不能实现焊合到挤出模孔过程的模拟分析［9-10］.为此，通常采用稳态挤压法或有限体法计算.稳态挤压法，建模时，假定金属坯料已经完成分流-焊合-成形(挤出型材头部)的3个阶段，根据计算所得的速度场、应力-应变场、温度场的分布情况来推断金属流动均匀性［11-13］.但由于忽略了分流与焊合过程，不能再现密闭的模腔内的金属流变过程，对于具有多个焊缝的复杂断面空心型材，仅根据获得场量布情况很难准确判断影响金属流动不均的主要因素.

有限体积法计算时不存在网格重划及穿透现象，但焊合时相互接触的网格单元仍不合并在一起，不能预测当焊合面两侧金属流速相差较大时，挤出型材产生弯曲和扭拧现象［14］.

为此，本文以Deform-3D有限元软件为计算平台，结合基于逆向工程技术的焊合面网格重构技术［15-16］，实现了焊合过程的模拟分析，并对异形管材分流模挤压的焊合过程进行了模拟分析.

1 焊合面网格重构技术

分流模挤压时焊合面开始接触并相互穿透时的网格单元模型如图1所示，挤压方向为沿图1中y轴的正方向.

网格修复准则依据塑性成形体积不变原理，当焊合面网格单元相互穿透区域和未穿透区域的体积相等时，删除相互穿透区域同时填补未充满区域，保证变形体网格模型重构前后体积不变.

焊合面网格的穿透模型如图2(a)所示.图2(b)为焊合面网格穿透区和尚未充满区域的几何示意图，其中阴影部分(实线边界的bdfe区域)为穿透区域，非阴影部分(实线边界的abc和fgh漏斗形区域)为尚未充满区域.

网格修复时，将图1(c)中Ⅰ区域所示的焊合面沿焊合室高度方向的轮廓简化为直线，则焊合面穿透区和尚未充满区域的体积可近似为:垂直于挤压方向的网格穿透区和未充满区域的面积(图2(b)中阴影区域和漏斗形非阴影区域)与焊合室高度的乘积.由于焊合室高度为定值，因此，可根据焊合面穿透区和尚未充满区域面积判断两者的体积是否相等.

由于图2(b)是为以实线为边界的阴影区域和漏斗形非阴影区域的弧线曲率及半径，在实际模拟过程中难以测量，面积精确计算也较为繁琐，因此，将图2(b)中阴影区域的面积简化为以虚线为边界的△bde和△fed的面积，漏斗形非阴影区域的面积简化为以虚线为边界的△abc和△fgh的面积.当 ac×bk+gh×fm=de×bo+de×fo 时，即△bde+△fed和△abc+△fgh的面积相等，开始对网格进行修复重构.

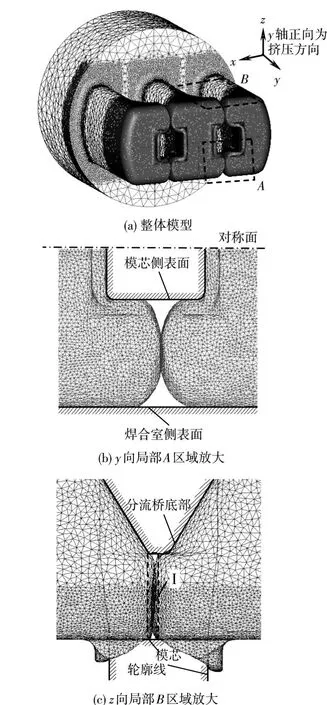
图1 焊合面网格相互接触时有限元模型

图2 焊合面单元网格相互穿透时修复准则

修复流程如图3所示.采用有限元软件Deform-3D计算时，当焊合面网格单元相互穿透区域和未穿透区域的体积相等时，将四面体网格模型转化成由三角形面片为描述单元的STL(Stereolithography)模型，通过Pro/ENGINEER软件中的基于逆向工程技术的小平面特征技术删除STL模型产生穿透及畸变的三角形网格，然后依次选取3个相邻的顶点重新构建三角形面片，同时将焊合面尚未充满区域用三角形面片单元进行填充，使得原始穿透区和未充满区重新形成STL模型，将此模型导入Deform-3D软件中重新进行四面体网格单元划分，如图4所示(网格重构前为图2)，然后添加历史计算的单元节点数据，完成焊合及成形过程的模拟分析.

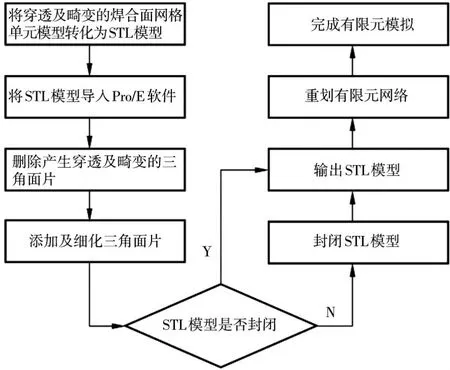
图3 焊合面网格修复流程

2 可行性与精度检验

2.1 几何模型构建

为了检验采用网格重构技术所得计算结果的可行性和精度，以方管为例，以焊合面设为刚性面的计算结果为标准，检验采用焊合面网格重构技术的计算结果.

方管尺寸、焊合面位置及模具结构示意图如图5所示.根据图5(b)所示的模具结构，焊合面与方管的对角线位置一致.当取 1/4模型(图5(a)中阴影部分)模拟时，计算对象内包含了焊合面，需采用网格重构技术，几何模型及网格划分如图6(a)所示.根据其对称性特点，当取1/8模型(图5(a)中阴影部分的一半)进行模拟，此时焊合面被简化为刚性面，计算时不会产生网格穿透现象，不需要进行网格修复，几何模型及网格划分如图6(b)所示.

方管尺寸为30 mm(L)×2 mm(t)，坯料直径为90 mm、挤压筒直径95 mm、挤压比31.6、分流比12.6.挤压的初始工艺条件为坯料(A6005铝合金)温度480℃、挤压筒温度400℃、模具(H13热作模具钢)温度450℃、挤压垫温度30℃，挤压轴速度4 mm/s.坯料和模具之间选用剪切摩擦模型，摩擦因子m=1.

图5 方管断面尺寸及分流模实体模型

图6 几何模型及网格划分

2.2 模拟结果对比分析

由图7的计算结果可知，从分流到焊合面开始接触阶段，采用1/4和1/8模型计算的结果相同，如图7(a)、(b)和(c)所示.

当挤压行程为30.95 mm时，采用1/4模型时，根据修复准则，此时焊合面相互穿透的网格单元区域和焊合面未充满区域面积相等，如图7(d)所示.重构后的焊合面网格如图7(f)所示.此时对应的1/8模型的计算结果如图7(e)所示，由于焊合面为刚性面，因此，无网格穿透现象，当挤压行程增为31.05 mm时，焊合面完全焊合，如图7(g)所示.

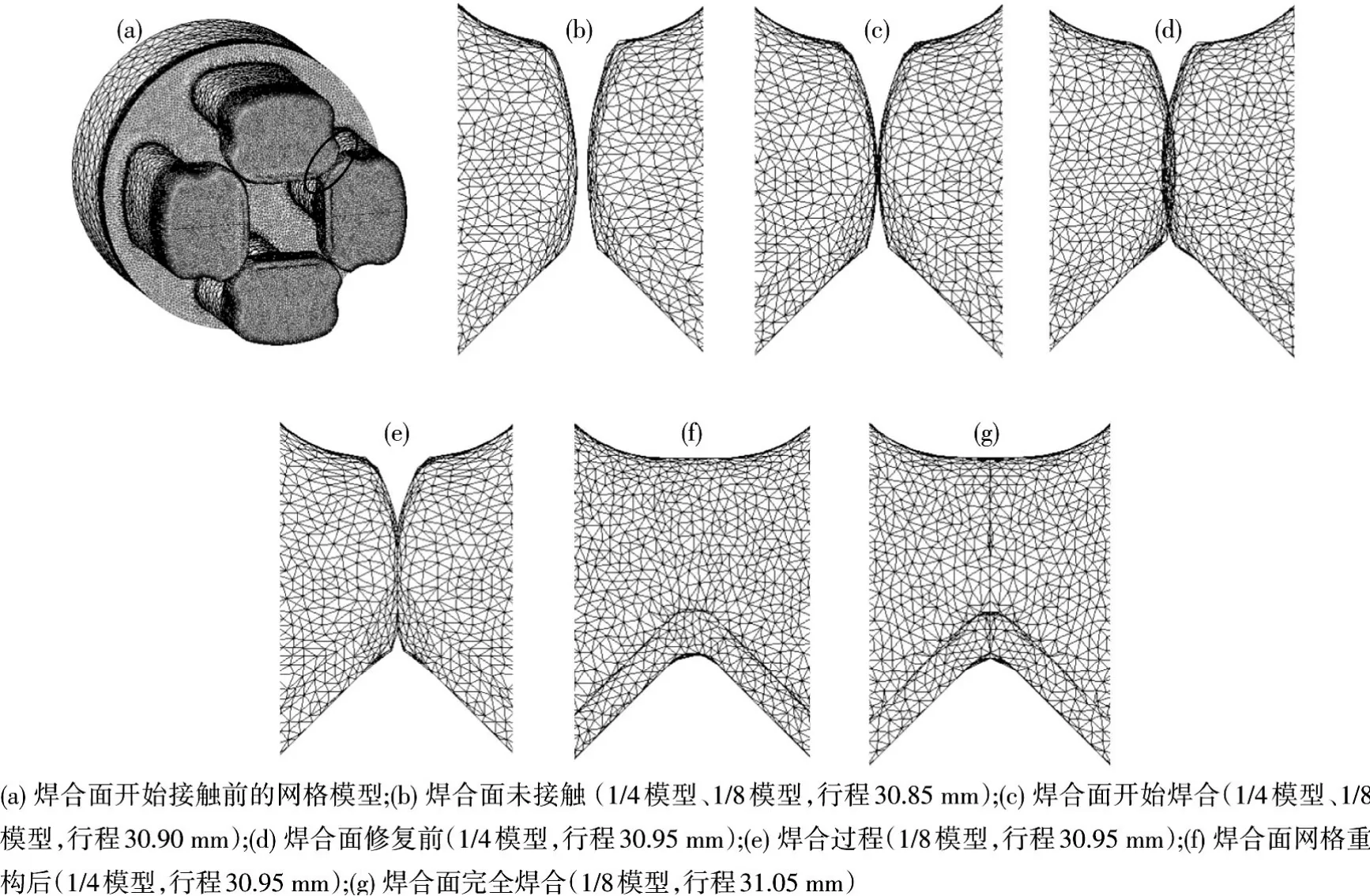
图7 焊合过程模拟分析

采用两种模型挤出的方管外形如图8所示.由图8可知，两种模型挤出的方管外形吻合较好.网格重构法与刚性面法的计算结果相比，仅相差了0.15 mm挤压行程，因此，对于计算结果影响较小.

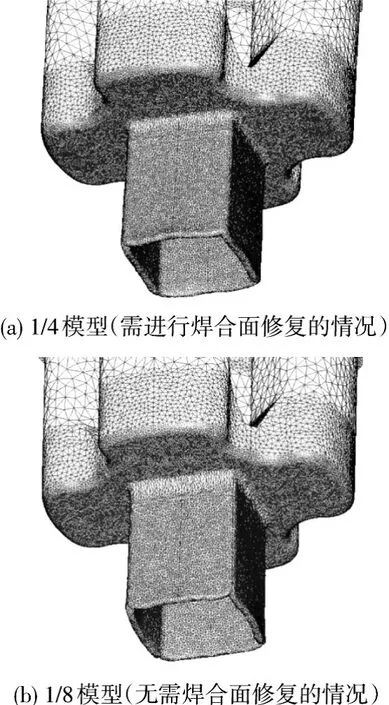
图8 挤出方管外形

挤压过程的温度分布是合理工艺制定的重要指标之一，采用两种方法获得的稳态挤压时温度场分布如图9所示.

图9 稳态时温度场分布

由图9可知，采用1/4模型和1/8模型，所得等温曲线分布结果在挤压筒内(Ⅰ)、模孔与挤出型材部分(Ⅲ)的基本一致，仅在分流孔和焊合室部位区域(Ⅱ)中有差异，但在此区间内两者的的温升(E-G线间)仅差1℃，同时整个模拟结果的温度仅差5℃.以无网格重构的1/8模型为比较基准，焊合面网格重构后计算所得温度场的偏差小于1%.

焊合室内静水压力是表征型材焊合质量的重要指标.采用1/4模型和1/8模型，稳态挤压时的静水压力分布如图10所示.由图10可知，两个模型计算所得的焊合室内的静水压力的分布基本相同，但数值上，1/4模型比1/8模型的计算结果高了7 MPa.以无网格重构的1/8模型为比较基准，网格重构后计算所得的静水压力场偏差小于2%.综合上述挤出型材外形、温度场及静水压力场的计算结果，可得本文的网格修复技术是可行的，具有满意的模拟精度.

图10 稳态时静水压力场分布

3 异形管材焊合过程模拟分析

3.1 网格重构

异形管材模具结构及尺寸如图11所示.由图11中上模的4个分流孔的配置可知，型材的焊合面位置与中心水平线成45°，因此，焊合面无法简化为刚性对称面，须采用本文提出的网格重构方法才能进行计算.坯料直径、挤压筒直径、摩擦边界条件及挤压工艺条件与2.1节中相同.挤压比为29.1，分流比为10.7.同时为了便于观测焊合室内焊合面位置，挤压前在模具内表面涂敷少量石墨乳.

图11 模具结构及主要尺寸意图

当挤压行程达到33.1 mm时，提取相互穿透的网格模型，如图12(a)所示，采用上述网格重构方法进行重构后的有限元模型如图12(b)所示.然后，在有限元软件Deform-3D中对重构模型添加单元节点数据，继续计算，完成焊合与成形过程的模拟分析.

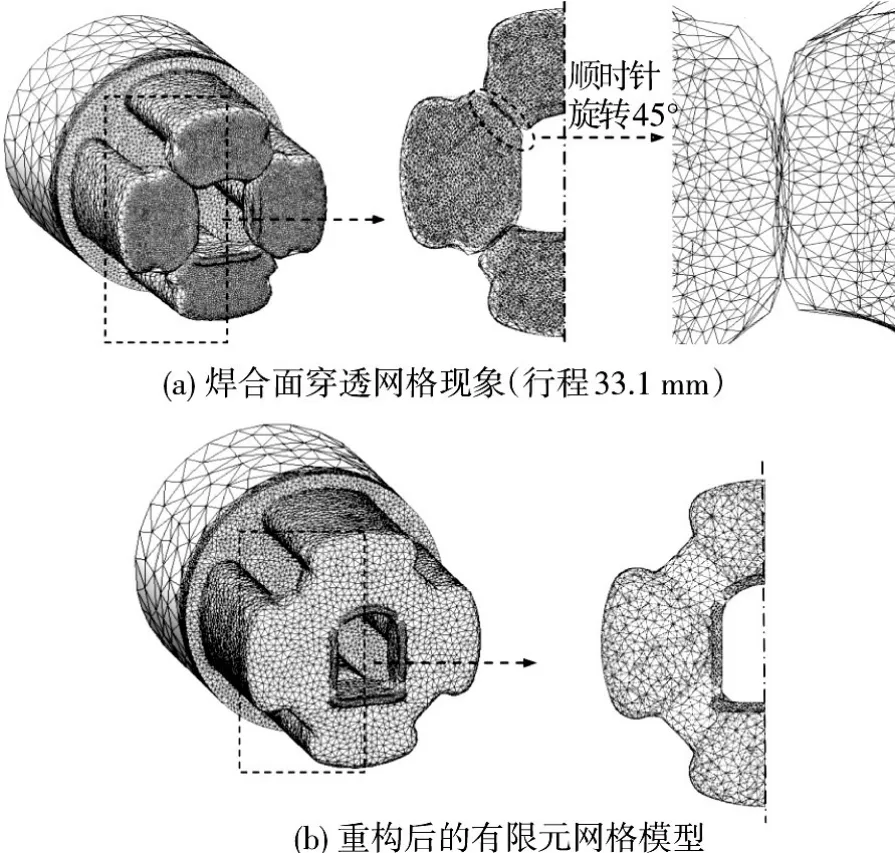
图12 焊合面网格重构情况

3.2 金属流动行为分析

图13为型材在挤压各阶段的金属流动行为.由图13可知，在分流阶段(图13(a))，金属在分流桥的作用下被拆分为4股进入分流孔，由于各分流孔面积、各分流孔与挤压筒中心距离基本相等，因此，分流孔内挤出金属的长度及流速基本相同.

在填充焊合阶段(图13(b))，4股金属相继与焊合室底面接触，形成径向流动并围绕模芯开始填充焊合室.从挤压焊合室的填充初始阶段到焊合完成的整个金属流动过程，如图13中(d)～(g)及(i)所示.随着挤压行程的增加，焊合面逐渐靠近，当挤压行程为32.9 mm时，焊合面开始接触.当挤压行程为33.1 mm时，开始采用本文提出的重构方法进行网格重构，即对于数值模拟结果，可认为已经完全焊合，如图13(g)所示.而此时实验的焊合情况如图13(h)所示.可见两者的焊缝位置吻合较好.

型材成形阶段，焊合室已经被金属完全填充满，如图13(i)所示.此时开始进入稳态挤压阶段，挤出的型材外形如图13(c)所示.

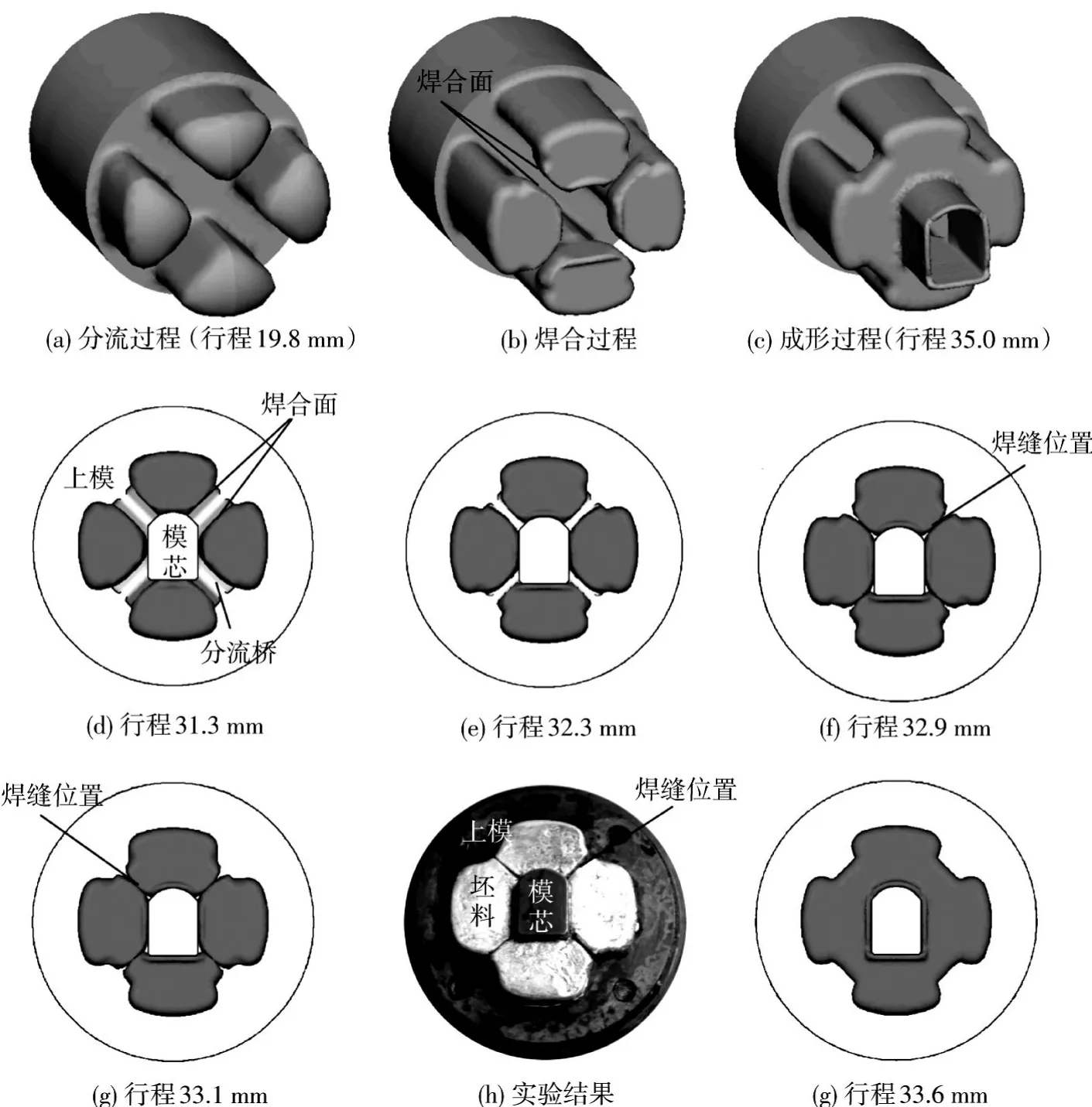
图13 挤压全过程金属流动行为分析

3.3 温度场分布

挤压稳态阶段，变形体的温度场分布如图14所示.由图14可知，沿挤压方向温度逐渐升高，焊合过程温度范围477～496℃，模孔附近达到最大值为515℃，比初始温度升高了35℃，而挤出型材的头部由于和外界存在散热使得温度下降.

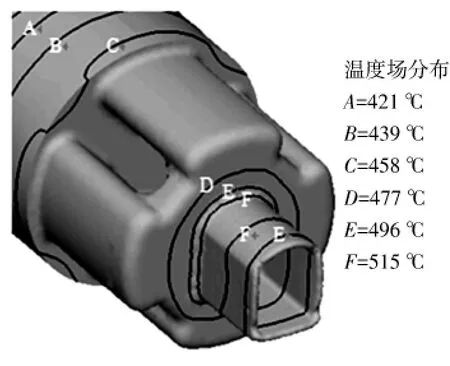
图14 温度场分布(行程35.0 mm)

3.4 焊合室内静水压力分布

分流模挤压过程中，焊合面上的静水压力越高，型材挤出的焊合质量就越好.稳态挤压时焊合室内金属变形体的静水压力分布如图15所示.

图15 焊合室内静水压力分布

由图15可知，焊合室内静水压力的分布由焊合室内壁向模芯逐渐减小，模芯周围最小静水压力为169 MPa，最大为343 MPa，而根据计算表明此时焊合室内最高温度约为496℃，在此温度下，A6005铝合金屈服强度约为45 MPa，其静水压力约为合金屈服强度的4～7.6倍，能满足焊合要求.

3.5 焊合过程模具应力分布

当焊合面开始产生接触焊合时，上模所受的等效应力分布如图16所示，可以看到，最大应力分布在分流桥焊合角D区，最大应力为205 MPa，远小于模具的抗拉强度，满足使用要求，模具结构设计合理.

图16 上模等效应力场分布(行程32.9 mm)

4 结论

1)采用Deform-3D有限元计算软件，根据焊合面简化为刚性对称面1/8模型与包含焊合面的1/4模型的方管分流模挤压计算结果可知，挤压焊合、成形过程金属流动行为两者吻合较好，温度场计算误差小于1%、焊合室内静水压力场误差小于2%，因此，网格重构技术具有较高的模拟精度.

2)获得了异形管材焊合过程的金属流动行为，当挤压行程为31.3 mm时，开始填充焊合室，行程为32.9 mm时，焊合面开始焊合，行程增加为33.1 mm时，焊合完成.

3)挤压时焊合室内温度为477～496℃，模孔附近达到最大值为515℃，比初始温度升高了35℃.焊合室内静水压力范围为合金屈服强度的4～7.6倍，能满足焊合要求.分流桥焊合角部位所受应力最大为205 MPa，远小于模具抗拉强度，模具结构设计合理.

［1］ 谢建新，刘静安.金属挤压理论与技术(第2版)［M］.北京:冶金工业出版社，2012.

［2］ 谢建新.金属挤压技术的发展现状与趋势［J］.中国材料进展，2013，32(5):254-263.XIE Jianxin.Current situation and development trends of metals extrusion technology［J］.Materials China，2013，32(5):254-263.

［3］ 李静媛，黄东男.三孔双芯模挤压方管型材的金属流动行为分析［J］.材料科学与工艺，2010，18(2):251-255，261.LI Jingyuan，HUANG Dongnan.Analysis of extrusion flow behaviors of square pipe deformed with threeporthole and two-core die ［J］.Materials Science and Technology，2010，18(2):251-255，261.

［4］ 邸利青，张士宏.分流组合模挤压过程数值模拟及模具优化设计［J］.塑性工程学报，2009，16(2):123-127.DI Liqing，ZHANG Shihong.Porthole die extrusion process numerical simulation and optimal die design［J］.Journal of Plasticity Engineering，2009，16(2):123-127.

［5］ 唐鼎，邹天下，李大永，等.亚毫米孔径微通道铝合金管挤压成形的数值模拟［J］.塑性工程学报，2011，18(3):25-29.TANG Ding，ZHOU Tianxia，LIDayong，etal.Numerical simulation study upon extrusion forming of microchanneltube［J］.Journal ofPlastIcity Engineering，2011，18(3):25-29.

［6］ LIU Peng，XIE Shuisheng CHENG Lei.Die structure optimization for a large，multi-cavity aluminum prof i le using numericalsimulation and experiments［J］.Materials and Design，2012，36:152-160.

［7］ ZHANG Shenggun，ZHAO Guoqun，CHEN Zhiren，et al.Effect of extrusion stem speed on extrusion process for a hollow aluminum prof i le［J］ .Materials Science and Engineering B，2012，117(19):1691-1697.

［8］ LIU G，ZHOU J，DUSZCZYK J.FE analysis of metal flow and weld seam formation in a porthole die during theextrusion of a magnesium alloy into a square tube and the effect of ram speed on weld strength ［J］.Journal of Materials Processing Technology，2008，200:85-98.

［9］ ZHANG Zhihan ，HOU Wenrong，HUANG Dongnan，et al.Mesh Reconstruction technology ofwelding process in 3D FEM simulation of porthole extrusion and its application［J］.Procedia Engineering ，2012，36:253-260.

［10］ 张志豪，谢建新.挤压模具数字化设计与数字化制造［J］.中国材料进展，2013，32(5):293-299.ZHANG Zhihao，XIE Jianxin.Digitaldesignand manufacture of extrusion die［J］.Materials China，2013，32(5):293-299.

［11］ 徐磊，赵国群，张存生，等.多腔壁板铝型材挤压过程数值模拟及模具优化［J］.机械工程学报，2011，47(22):61-68.XU Lei，ZHAO Guoqun，ZHANG Cunsheng，et al.Numerical simulation of extrusion process and die optimization for aluminum multi-cavity profile［J］.Journal of Mechanical Engineering ，2011，47(22):61-68.

［12］ 喻俊荃，赵国群，张存生，等.阻流块对薄壁空心铝型材挤压过程材料流速的影响［J］.机械工程学报，2012，48(16):52-58.YU Junquan，ZHAO Guoqun，ZHANG Cunsheng，et al.Effect of baffle-block on material flow velocity during thin-walled hollow aluminum profile extrusion［J］.Journal of Mechanical Engineering ，2012，48(16):52-58.

［13］ 宋佳胜，林高用，贺家健，等.列车车体 106XC型材挤压过程数值模拟及模具优化［J］.中南大学学报(自然科学版)，2012，43(9):3372-3379.SONG Jiasheng，LIGaoyong，HE Jiajian，etal.Numerical simulation of extrusion process and die optimization of 106XCaluminum body profile for track vehicle［J］.Journal ofCentralSouth University(Science and Technology)，2012，43(9):3372-3379.

［14］ 和优锋，谢水生，程磊，等.黄蝶形模具挤压过程的数值模拟［J］.中国有色金属学报，2011，21(5):995-1001.HE Youfeng，XIE Shuisheng，CHENG Lei，et al.Numerical simulation of butterfly die extrusion process［J］.The Chinese Journal of Nonferrous Metals，2011，21(5):995-1001.

［15］ 谢建新，黄东男，李静媛，等.一种空心型材分流模挤压焊合过程数值模拟技术［P］.中国:200910088960.7，2009-07-15.

［16］ HUANG Dongnan，ZHANG Zhihao，LI Jingyuan，et al.FEM analysis of metal flowing behaviors in porthole die extrusion based on the mesh reconstruction technology of the welding process［J］.International Journal of Minerals，Metallurgy and Materials，2010，17(6):763-769.