凸轮挺柱摩擦副接触应力的仿真计算

2015-11-30唐其超卢继平

装备制造技术 2015年11期

唐其超，周勇，卢继平

（北京理工大学机械与车辆学院机电一体化中心，北京100081）

凸轮挺柱摩擦副是发动机三大摩擦副之一。随着发动机功率密度的日益提高，凸轮挺柱摩擦副常常要工作在高压、润滑不足、震动大、接触应力大的工况下。这会导致凸轮挺柱表面的剧烈磨损，同时严重影响了配气机构的工作精度和发动机的充气效率，即大大降低了发动机的动力性能和经济性能[1]。凸轮挺柱的磨损不仅影响配气机构换气性能，而且会增加噪音，最终影响整个发动机的寿命[2]。

对配气机构进行计算，应首先建立计算模型。参考文献中有单质量模型、二质量模型、多质量模型等多种建模方法。单质量模型是最早被建立的，其综合考虑了各零件的传动变形和质量，结构简单，计算方便。其使用一个集中质量表示内燃机的配气机构，由气门杆到凸轮轴的刚度作为系统刚度，传动零件各部分的阻尼作为系统阻尼。经过大量实践证明，采用实测参数运用单质量模型进行计算，获得的结果与试验数据非常接近。

本文选用单质量模型对装甲车高功率密度发动机进行配气机构的柔性动力学计算，得到凸轮挺柱间接触应力。而后，分别运用赫兹接触理论和有限元仿真的方法，得到凸轮表面的接触应力。

1 配气机构动力学分析的模型建立

1.1 配气机构气门运动分析模型的建立

如图1所示，单质量模型使用一个集中质量来表示配气机构，集中质量的运动表示配气机构气门的运动。该集中质量为配气系统各部分质量换算至气门一侧的当量质量之和。因凸轮刚度大，将凸轮作刚体处理，图示中凸轮为当量凸轮，即将挺柱一侧的凸轮升程换算至气门一侧。各部分之间由气门弹簧，以及系统“弹簧”相连。单质量模型中，配气机构的质量以集中质量M来表示。M的质量包括气门的质量、气门弹簧上座的质量、弹簧座卡子的质量、摇臂转动惯量转换至气门处的当量质量、推杆转换至气门处的当量质量、挺柱转换至气门处的当量质量[3]。

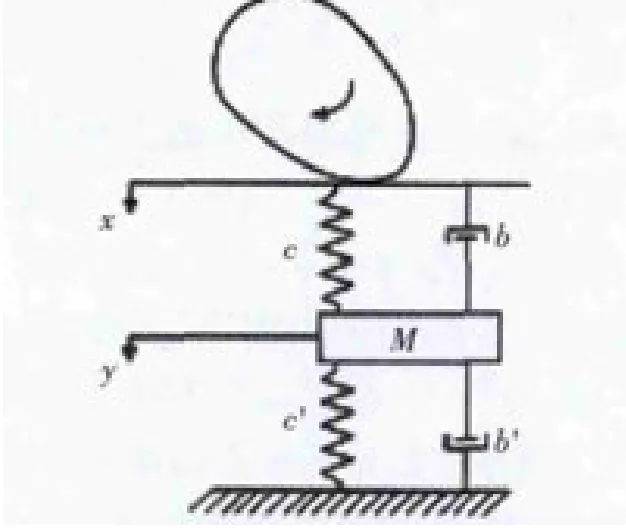
图1 配气机构单质量模型

上图中，

c表示配气机构传动链的弹性；

b表示配气机构传动链的阻尼力，即内阻尼力；

c'表示配气机构气门弹簧的弹性；

b'表示气门弹簧的阻尼，即外阻尼力；

M的一端通过弹簧c'与缸体连接，另一端通过“弹簧”c与当量凸轮连接。

当量凸轮升程函数为：

其中，s（α）为凸轮实际升程函数，k为摇臂比。

要获得气门的升程函数，即获得集中质量M的位移 y对应凸轮转角α的表达式y（α）的微分方程，并给出初始条件。

设作用在集中质量上的外力总和为F，则

即：

外力F包括以下几个部分：

一是配气机构弹性恢复力 c·[y（α）-x（α）]；

二是气门弹簧的弹力-c'·y（α），负号表示力的方向相反；

三是气门弹簧预紧力-F0；

四是内阻尼力 b·w·JV，其中：JV=d x/dα -d y/dα

五是外阻尼力-bp·ω·（d y/dα）

将以上各力代入式（3），可得：

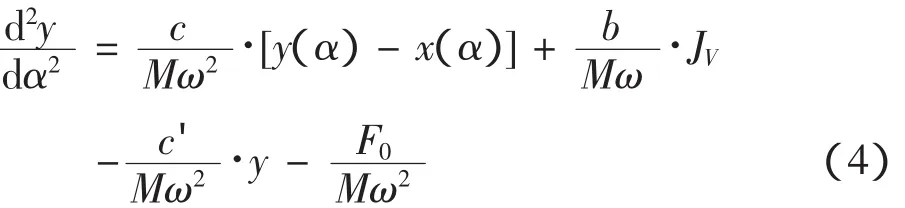
这是一个关于未知函数y（α）的二阶常微分方程，有无穷多个解。为了得到气门升程函数y（α），需要给出两个初始条件，即气门刚刚开启瞬间有：

1.2 配气机构凸轮挺柱摩擦副接触力模型的建立

在凸轮挺柱工作表面接触应力的计算过程中，也分为刚体运动学方法和柔体动力学方法。

（1）凸轮挺柱之间作用力刚性运动学分析方法

运动学计算方法的模型如图2所示，其将整个配气机构视为完全刚性的，而不计其弹性变形。图中M’为配气机构换算至挺柱侧的当量质量，弹簧和阻尼分别为气门的弹簧和阻尼换算至挺柱侧的当量值。

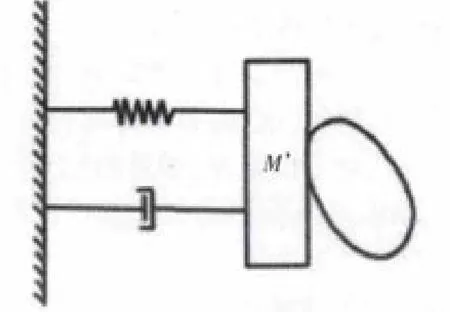
图2 凸轮挺柱接触力运动学计算模型简图

运动学的计算方法中，凸轮挺柱之间的接触力F将取作传递到凸轮上的弹簧力FC和换算至挺柱处的配气机构运动零件惯性力FN之和。系统外阻尼为0，所以不计系统外阻尼。可得接触力计算公式：

其中FC为气门弹簧弹力换算至凸轮侧的值。

FN为整个系统换算至凸轮挺柱一侧的惯性力。

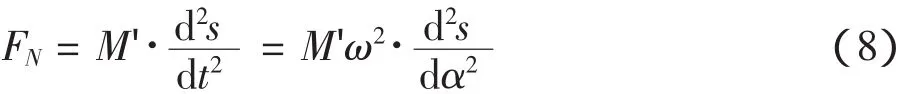
其中M'为配气系统质量换算至凸轮挺柱侧的质量。

最终可得凸轮挺柱接触力：

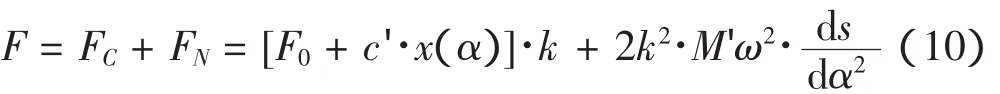
（2）凸轮挺柱之间作用力柔性动力学分析方法

上述运动学计算方程将配气机构完全作为刚性，对于高功率密度发动机，则往往不能忽略其传动链的弹性变形，运用动力学的计算方法可以得到相对准确的结果。

考虑到配气机构的弹性变形，此节中利用单质量模型进行凸轮挺柱间接触力的计算。如图3所示为建立凸轮挺柱的动力学模型。与配气机构气门分析单质量模型不同，此模型中质量m是由凸轮直接驱动的当量质量，取挺柱质量与半个推杆质量之和。

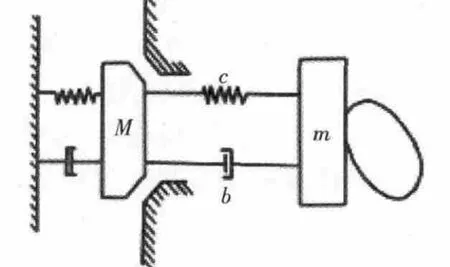
图3 凸轮挺柱接触力动力学计算模型简图

此模型中凸轮与挺柱之间的接触力为：

综上，可得由动力学计算方法得到凸轮与挺柱直接接触力。

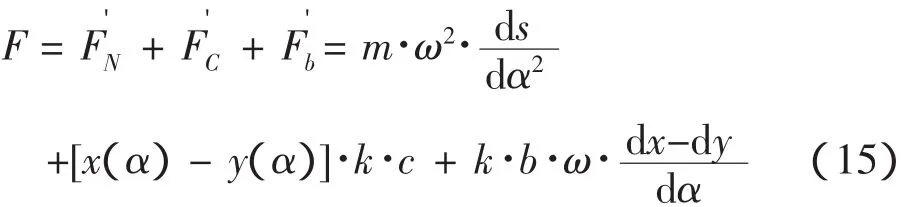
2 凸轮挺柱动力学仿真的前置处理

2.1 凸轮升程曲线确定

本文取多项式凸轮升程曲线，其表达式为：

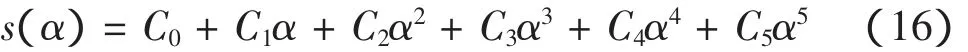
其中 s（α）为挺柱升程，α 为凸轮转角，C0、C1、C2、C3、C4、C5为待定系数。

对式（16）分别求一阶、二阶导数可得凸轮升程速度函数：

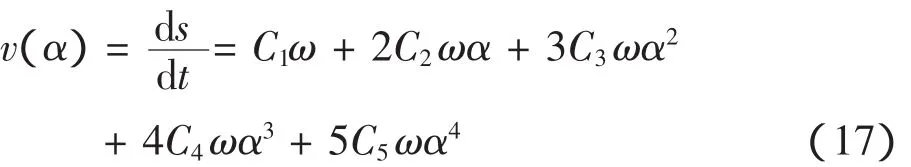
加速度函数为：

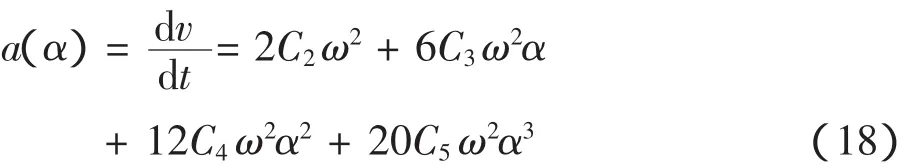
其中ω为凸轮转速，根据发动机的实际工况，取发动机转速为2 000 rad/min，凸轮轴转速为发动机曲轴转速一半，所以ω=1000 rad/min=6 000°/s.

当时α=7，系统速度，加速度为0，可得初始条件：

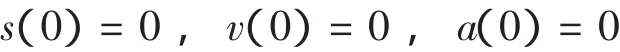
取α=70时，挺柱升程为最大值7mm，则有初始条件：

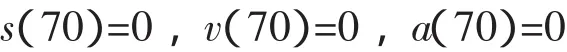
将以上条件带入式（16）、式（17）、式（18）中，在MATLAB中可解方程，得：

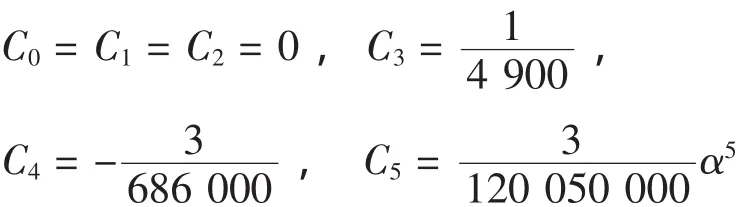
可得升程曲线函数为：

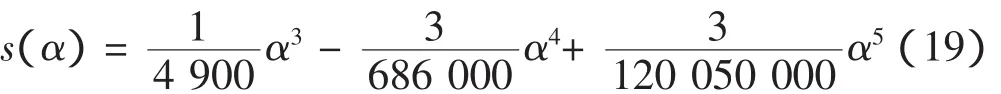
在MATLAB中绘制挺柱上升阶段的升程曲线，如图4所示。

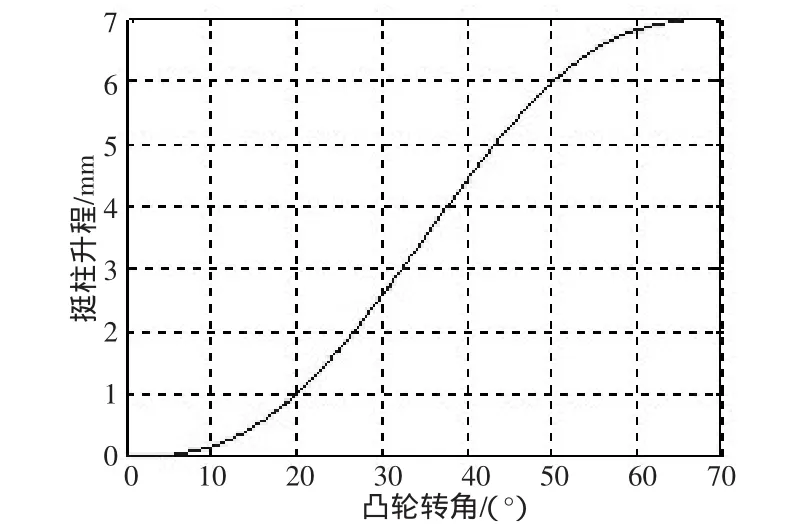
图4 凸轮升程曲线

由式（17）绘制发动机转速为 2000 rad/min时挺柱运动的速度曲线，如图5所示。在整个运动过程中，速度没有突变，则表明凸轮挺柱之间没有刚性冲击，可以减轻凸轮的震动和磨损。

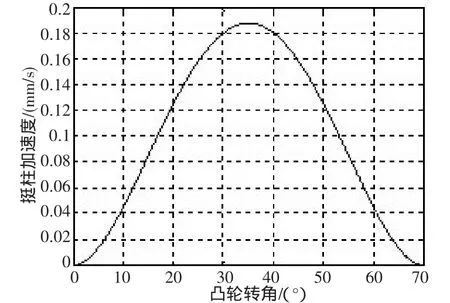
图5 凸轮升程速度曲线

由式（18）在 MATLAB中绘制凸轮转速为 1000转时挺柱运动的加速度曲线。如图6所示，从图中可以看到挺柱在上升过程中，其运动的加速度没有突变，即没有柔性冲击。说明多项式凸轮曲线使凸轮与挺柱之间冲击小，系统运行平稳。

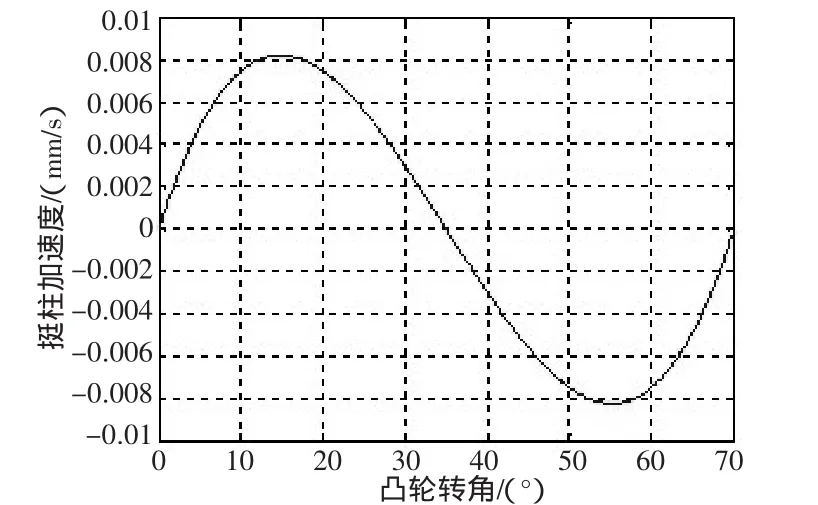
图6 凸轮升程加速度曲线

3 凸轮挺柱摩擦副表面接触应力的仿真分析

3.1 接触力分析

利用式（10）和式（15），对凸轮挺柱间的接触力分别进行刚体运动学计算和柔体动力学计算，分别得到挺柱上升阶段凸轮挺柱之间接触力随凸轮转角的变化，如图7所示。

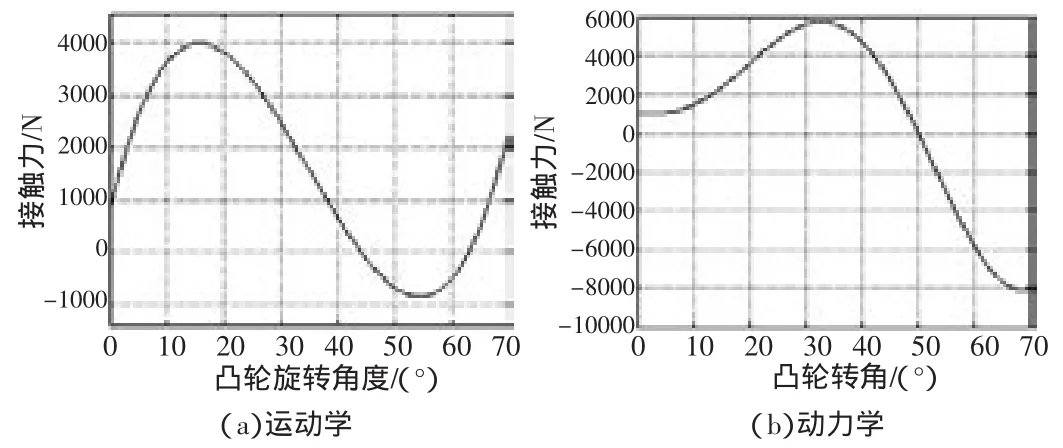
图7 凸轮挺柱间接触力曲线

从图中可以看出，在刚性模型的计算中，刚性模型最大的接触力发生在15°左右，约为4 000 N；柔性模型中最大接触力发生在 33°左右，约为 5 500 N.由于配气系统弹性作用，柔性动力学模型接触力的变化较慢，在开始变化时较刚性模型变化较小，但其最大值大于刚性模型的计算值。配气系统刚性运动学分析中，在凸轮升程过程中40°至62°凸轮挺柱的接触力为负值，即挺柱脱离了凸轮；在柔性动力学模型中，凸轮在50°至70°时，凸轮与挺柱间接触力为负值，发生了飞脱。挺柱的飞脱会对凸轮挺柱造成摩擦副造成很大的冲击，使凸轮挺柱之间不断发生碰撞，并发出噪声，配气系统此时运行在极不稳定的状态。此种情况加快了配气机构的磨损失效，在设计凸轮升程时应尽量避免。重新设计合理的凸轮升程曲线，降低发动机的转速可以减少此类情况的发生。

3.2 凸轮接触应力分析

将上述接触力带入赫兹公式[4]，可分别得到挺柱上升阶段凸轮挺柱之间最大接触力随凸轮转角的变化，如图8所示。从图中可以看出当接触力出现负值时，即挺柱发生飞脱时，接触应力为零。运动学模型中，接触应力值快速上升到一定值，然后小幅下降，发生了较快的波动，最大应力值出现在30°左右。由于柔性动力学模型系统弹性的作用，凸轮挺柱间接触应力出现了小幅的下降，随后一直上升，其最大应力值出现在40°左右，且相对于刚性模型的接触应力最大值更大。在达到最大值后，两模型的接触应力都迅速下降至0，即很快发生了挺柱的飞脱。