串联型混合动力船舶能量控制策略研究
2015-11-29李洪跃
李洪跃,朱 瑾
(上海海事大学 航运技术与控制工程交通行业重点实验室,上海 201306)
串联型混合动力船舶能量控制策略研究
李洪跃,朱 瑾
(上海海事大学 航运技术与控制工程交通行业重点实验室,上海 201306)
如何分配混合动力电动船舶中柴油发电机组与燃料电池之间的能量,对提高船舶经济性和减少能耗至关重要。为了解决这个问题,提出用动态规划方法优化两种动力源的输出功率。首先建立船舶组件的数学模型。然后,基于贝尔曼最优化原理,以最小燃油消耗为目标函数得到柴油发电机组的最优控制序列。仿真结果表明,与开关式控制策略相比,动态规划算法可以合理分配输出功率,使电池SOC保持稳定,有效降低船舶的耗油量。
混合动力电动船舶;能量控制;荷电状态;动态规划
0 引言
在未来船舶技术的研究中,以电力推进系统为主的纯电动船舶将被大力发展。然而受到储能技术、船舶重量和船舶空间等方面因素的限制,纯电动船舶的续航能力、自控性、船速和加速度等指标不能达到要求[1]。基于上述情况,混合动力推进技术的研究可以为船舶发展从柴油发电机供电系统过渡到纯电动系统提供可行性方案,有助于解决柴油发电机组船舶能源消耗问题与纯电动船舶局限性问题之间的矛盾。
与传统的以柴油发电机组为动力源的船舶相比,混合动力电动船舶能有效地减少燃油消耗。这是因为:1)混合动力推进系统允许选用功率较小的发动机;2)能够实现制动能量回馈;3)混合动力推进系统中存在两种动力源,增加了自由度,对于一定的功率需求,可以由控制算法决定各动力源输出功率的大小分配。目前对混合动力推进器研究较早的有“开关式”和“功率跟随式”两种方法[2-5]。但是这两种方法都只能达到某种意义上的次优控制[6]。基于规则的模糊逻辑控制结合了“开关式”和“功率跟随式”两种方法的优点[7],但是规则的提取需要大量的先验知识,计算量大,实时性不好[8]。通过以上分析,本文提出用动态规划的方法,利用贝尔曼最优化原理得到全局最优控制策略。
通过以上分析,本文提出用动态规划的方法。首先对混合动力电动船舶的动力系统进行建模,然后通过一段已知工况的驾驶循环,对数学模型进行求解。根据贝尔曼最优化原理,优化柴油发电机组和电池的输出功率,使得电池SOC保持在预先设定水平,得到全局最优解。
1 串联型混合动力电动船舶动力结构与配置
混合动力电动船舶的动力源由柴油发电机组和蓄电池两部分组成,按照连接结构可分为串联、并联和混联三种。本文采用串联型混合动力电动船舶作为研究对象,其结构图如图1所示。

图1 串联型混合动力电动船舶结构图
串联型混合动力电动船舶的功率流图如图2所示。规定电池放电过程的输出功率为正,充电过程的吸收功率为负。由于柴油发电机组始终输出功率,因此为正。功率流动满足等式:

式中,Pe(t)为t时刻柴油发电机组的输出功率;Pb(t)为t时刻电池的输出功率;Pel(t)为t时刻船舶电气负载的消耗功率,假设其为定值;Preq(t)为t时刻船舶需求功率。

图2 串联型混合动力船舶功率流图
为了找到柴油发电机组和蓄电池的最佳输出功率分配路径,首先需要对船舶各个系统进行建模。在模型建立的过程中,我们忽略外部条件对发动机、发电机和电动机的影响,只考虑其静态特征进行建模。
1.1 柴油发动机模型
船舶柴油发电机组由柴油发动机和发电机组成,它以柴油发动机为原动力带动发电机发电。把燃料的化学能转化为动能,再将动能转化为电能。本文采用数值模型法建立发动机的静态模型。发动机在t时刻的理论燃油消耗为:

式中,Pe为发动机功率;Te为发动机转矩;ωe为发动机转速;Te_corred为发动机修正转矩;Je为发动机转动惯量;b为发动机的燃油消耗率。
1.2 电机模型
在混合动力推进系统中,电机需要工作在电动机和发电机两种模式下。当电机工作在柴油发电机组和为电池充电时,看作为发电机;当电机将电能转化为动能带动螺旋桨转动驱动船舶时,看作为电动机。
电机工作在发电机模式时的功率为:
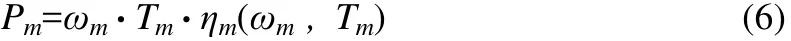
电机工作在电动机模式时的功率为:

式中,Pm为电机功率;ωm为电机转速;Tm为电机转矩;ηm为电机的平均效率,实验证明ηm是ωm和Tm的函数,其值可以通过电机的万有特性曲线图得到。电机在K时刻的能量消耗,等效为燃油消耗:
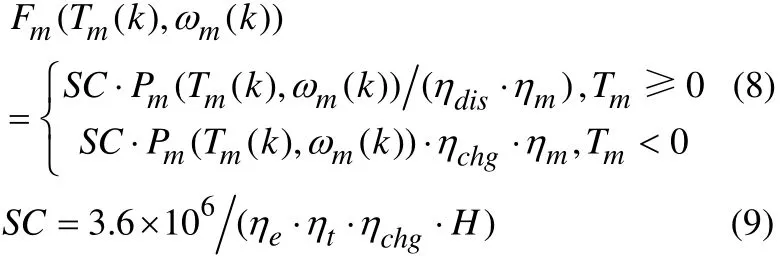
式中,ηchg、ηdis、ηm、ηe分别为电池充电效率、电池放电效率、电机效率和发动机效率;SC为油电平均转换效率;H为燃油低热值。
1.3 电池模型
电池是混合动力推进系统的能量源之一,它能够迅速响应负载变化,使得需求功率与输出功率保持平衡。电池的荷电状态SOC表示电池剩余容量与其完全充电状态的容量的比值,取值范围为0~1,当SOC=0时表示电池放电完全,当SOC=1时表示电池完全充满。本文采用电池内阻模型作为估算电池荷电状态SOC的模型,将电池等效为理想电压源Voc和电阻Rb的串联,忽略温度对电池SOC的影响。电池内阻等效电路如图3所示。蓄电池荷电状态SOC计算公式如下:
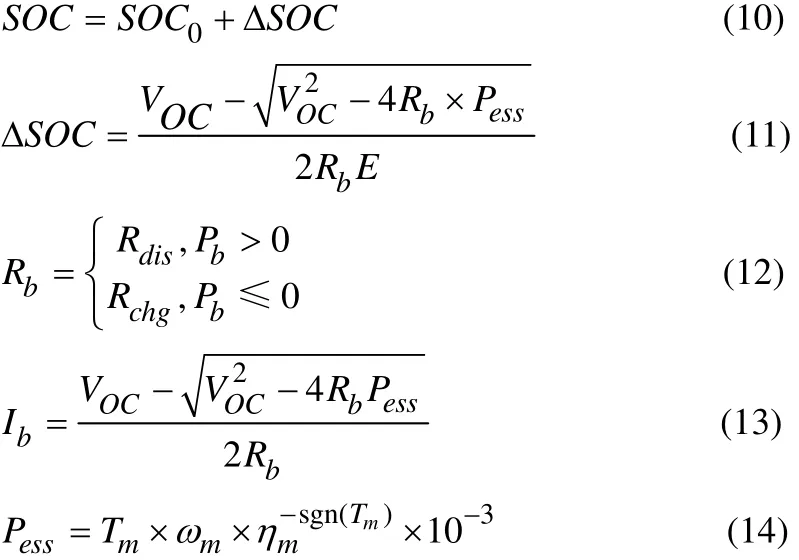

图3 电池内阻等效电路
其中,SOC0表示SOC的初始值;ΔSOC表示SOC的改变量;Ib为电池的端电流;E为电池的额定容量;Pess表示电机有效充放电功率;Voc表示电池等效电路理想电压源;Rb为电池内阻。在电池充电或者放电的过程中,其等效电阻Rb的值是不一样的,当电池荷电状态 SOC保持在 0.3~0.8时,可以近似的看为Rb=Rdis=Rchg。
1.4 系统约束条件
系统总成各部件需要满足约束条件如下:

2 动态规划算法
2.1 动态规划数学模型
动态规划算法是求解多阶段决策过程最优化的数学方法,核心为贝尔曼最优化原理,其适用条件必须满足最优化原理和无后效性原理。能量控制问题的求解过程首先要将其离散化,设整个工况的运行时间为[0,T],离散为步长为ΔT的N份时间序列;电池SOC取值范围为[SOCmin,SOCmax],离散为步长为ΔSOC的M份数值序列。离散后的网格图如图4所示。

图4 离散化网格图
电池SOC可以表示各个时段能量的变化,因此可以选取SOC的变化作为状态变量x(k),选取电机转矩Tm(k)和电机转速为ωm(k)决策变量u(Tm(k),ωm(k));由式(10)~(13)得,离散化的系统状态方程为:

由式(2)、(8)得系统在K时刻的总的燃油消耗为:

因此系统在工作时域内的总燃油消耗为:

引入惩罚函数 G[SOC(k)]=α[SOC(k)-SOCf]2,系统的最终目标函数为:
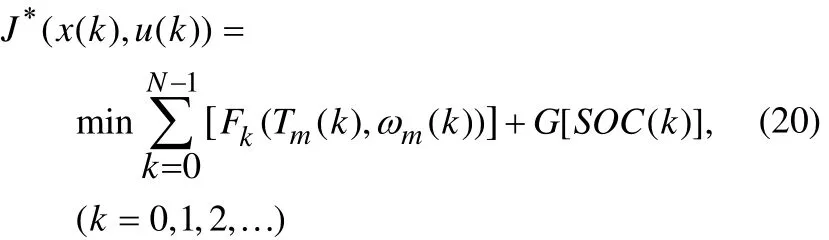
2.2 动态规划问题的求解
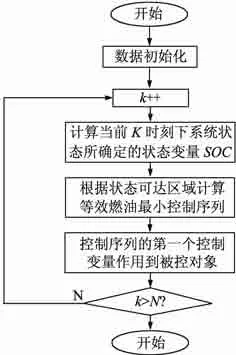
图 5为基于动态规划算法的流程图。在工作时域内的最优化问题通过动态规划分解为如下系列简单问题:
1) i步骤:
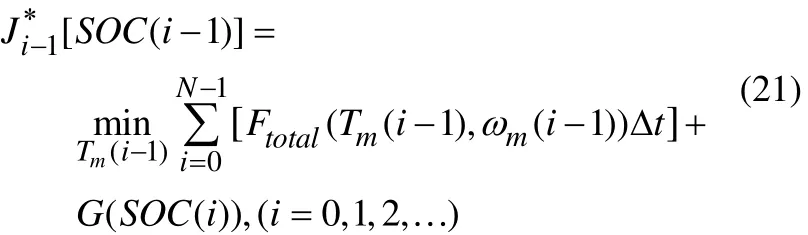
2) k(k J*k[SOC(k)]是状态 SOC(k)下的最优函数,为 k阶段的最优结果。通过这种逆序算法可获得k到k+Δt时域内的最优控制序列。基于动态规划方法的能量管理策略基本步骤如下: 图5 基于动态规划算法的流程图 1)获取当前k时刻的系统参数、需求转矩、转速及电池SOC等; 2)在当前k时刻,根据k+Δt时刻路况的需求功率信息,计算电池SOC的改变量ΔSOC; 3)在 Δt时刻里以燃油最小为目标进行局部的最优计算,通过贝尔曼动态规划化计算,可获得k+Δt时域内的最优控制序列{u(k+1),u(k+2),…}; 4)将最优控制转矩序列的第一个值u(k+1)作为下一时刻的控制变量作用于被控电机; 5)返回步骤1,重复计算过程直到达到设定条件。 为了验证该方法的有效性,我们用MATLAB软件对该方法进行仿真。仿真中选用最大功率为100kW的2冲程发动机;发电机额定转速为850r/min,发电机效率为96%;电池组选用80Ah,额定电压为320V,电池内阻25mΩ,设定电池组初始SOC值为0.6。 本文通过记录一组混合动力推进船在湖泊里的一段航行数据进行分析。首先用动态规划方法对行驶工况进行仿真,再通过开关式能量管理策略仿真结果进行比较。 图6为根据记录的航行数据得到的功率需求曲线。在整个航行周期内,以动态规划控制策略和开关式控制策略得到的结果进行比较。通过计算可以得到在整个航行周期内,以动态规划方法为控制策略的油耗量为26.95L,以开关式为控制策略的油耗量为26.15L。从图7中可以看出,动态规划控制下发动机输出功率比开关式控制更为平稳。图8说明动态规划算法控制下电池SOC的最大值和最小值保持在0.5到0.65之间,波动幅值更小,更有利于电池的安全性和增加寿命周期。 图6 需求功率曲线图 图7 两种控制算法下发电机输出功率比较 图8 两种控制算法下电池SOC的变化曲线 从仿真结果可以看出,在动态规划方法的控制策略下,柴油发电机组并不是一直工作在固定的输出功率上,也不是以机械的方式跟随需求功率的变化输出功率,而是根据每一阶段最优的等效油耗值得到的最优控制序列,通过电池补充柴油发电机组输出功率与需求功率之间的差值。这样减少电池的充放电次数,从而减少充放电过程中的能量损耗。在150s的测试周期中,动态规划算法比开关式控制策略省油约0.8L。 [1] 孙彦琰, 高迪驹,褚建新. 混合动力电动船舶模糊逻辑控制策略[J]. 船舶工程, 2014, 36(3): 67-70. [2] Sciarretta A, Back M. Guzzella L. Optimal control of parallel hybrid electric vehicles[J]. IEEE Transactions on Control Systems Technology, 2004,12(3): 352-363. [3] Anderson C, Pettit E. The effects of APU characteristics on the design of hybrid control strategies for hybrid electric vehicles, SAE Paper,950493[R]. USA: Society of Automotive Engineers,1995:65-71. [4] Stefano B. Techniques to control the electricity generation in a series hybrid electric vehicle[J].IEEE Transactions on Energy conversion, 2002,17(2): 260-266. [5] Bargar H, Li Jingbo, Goering D J, et al. Modeling and verification of hybrid electric HMMWV performance[C] //Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Society. New York: IEEE, 2003: 939 -944. [6] Del Pizzo A, Polito R M, Rizzo R, et al. Design criteria of on-board propulsion for hybrid electric boats [C]// XIX International Conference on Electrical Machines, 2010. [7] Jaliln, Akheir N, Salman M. A rule-based energy management strategy for a series hybrid vehicle[C]//Proceedings of the 1997 American Control Conference. Albuquerque, NM, USA: IEEE, 1997:689-693. [8] 肖仁鑫,李 涛,邹 敢,等. 基于随机动态规划的混联式混合动力汽车能量管理策略[J]. 汽车工程,2013, 35(3): 317-321. Research on Energy Control Strategy of Series Hybrid Ship LI Hong-yue, ZHU Jin How to distribute the energy between the diesel generator and the fuel cell of the hybrid electric ship is very important to improve the economy of ships and to reduce energy consumption. To solve this problem, it is put forward that the output power from the two different sources is optimized by using the dynamic programming (DP) algorithm. Firstly, the mathematical model of the ship is established. And then, based on Bellman's principle of optimality,taking the function of minimum fuel consumption as objective, the optimal control sequence of the diesel generator is obtained. The results show that, compared with the switch control strategy, the DP algorithm can distribute the energy reasonably, the battery SOC remains stable, and the fuel consumption of the ship reduces effectively. hybrid electric ship; energy control; state of charge; dynamic programming U664.14 A 10.16443/j.cnki.31-1420.2015.01.006 上海海事大学科研基金项目资助(20120089) 李洪跃(1990-),男,在读硕士。研究方向:混合动力船舶能量管理策略。 朱瑾(1980-),女,博士、副教授;主要从事船舶、港口自动化、生产与物流系统建模与优化、智能计算。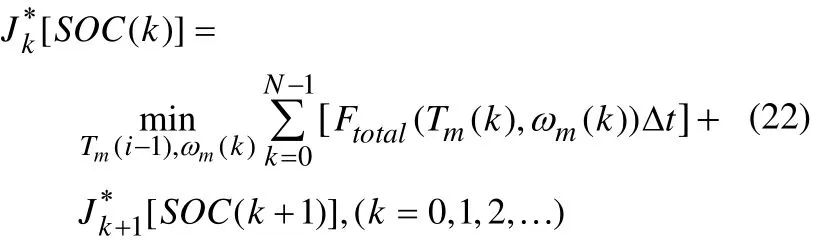
3 仿真结果



(Key Laboratory of Marine Technology and Control Engineering Ministry of Commmunications, Shanghai Maritime University, Shanghai 201306, China)
