基于航道与泊位资源协调调度的船舶交通优化
2015-11-29张新宇郭子坚王金涛大连海事大学航海动态仿真和控制交通行业重点实验室辽宁大连606大连理工大学水利工程学院辽宁大连603
张新宇, 郭子坚, 王金涛, 林 俊(. 大连海事大学 航海动态仿真和控制交通行业重点实验室, 辽宁 大连 606; . 大连理工大学 水利工程学院, 辽宁 大连 603)
基于航道与泊位资源协调调度的船舶交通优化
张新宇1,2, 郭子坚2, 王金涛1, 林 俊1
(1. 大连海事大学 航海动态仿真和控制交通行业重点实验室, 辽宁 大连 116026; 2. 大连理工大学 水利工程学院, 辽宁 大连 116023)
将港口航道与泊位资源协调利用,可最大限度地提高港口运营效率。对此,以所有船舶总在港时间和等待时间最少为目标,建立基于单向航道的多目标船舶调度优化模型。根据港口不同区域的交通流特征,建立初始化约束、流量转换约束、时隙分配约束和泊位冲突消解约束等多个约束模型。设计多目标遗传算法进行求解,并设计有针对性的模拟场景进行验证;以港口某一繁忙时段的20艘船舶为例,进行调度试验。最终得到8个Pareto最优解和2个目标的最优解:总调度时间为2.618 6 h,添加惩罚后总等待时间为23.012 4 h。结果表明:该模型及算法给出的调度方案能有效提高船舶的调度效率。
水路运输; 单向航道; 船舶调度优化; 多目标遗传算法; 时隙分配; 流量转换
海上运输是目前国际货物运输中最主要的方式,其服务质量很大程度上受港口对船舶进出港服务效率的影响。目前关于船舶进出港调度的研究主要侧重于航道流量和泊位分配中的单一方面,而对于两者协调调度的研究相对较少。
在航道通过能力方面:邵俊岗等[1]运用排队论对港口通过能力进行了综合评估;李子强[2]通过分析交通流,对航道通过能力进行了研究;代君等[3]运用船舶领域模型对港口受限航道通过能力的计算方法进行了探讨。这些研究针对的是静态模型,不能反映动态交通情况。此外,张玮等[4-6]分别针对苏北大运河、长江三峡和葛洲坝的单向航段进行了规划研究,研究重点是通航闸口管制,无须考虑航道通过时间,并不适用于单向航道的船舶调度问题。
在航道使用效率方面:徐国裕等[7]根据船载自动识别系统(Automatic Identification System,AIS)提供的与船舶航行安全相关的资料,以泊位远近、船舶大小、船舶类型和船舶吃水等因素为权重,提出了单向水道船舶进出港最佳排序模式;LLOYD等[8-9]对保持安全水域空间、构建整合系统和减少排序冲突给予了充分关注;OZGECAN等[10]采用多种排队模型分析了伊斯坦布尔海峡的狭长水道内船舶航行的风险和效率,并针对水道中突发的交通阻塞问题进行了多种中断排队优化。PULUGURTHAL等[11]从航道流量角度进行了船舶调度优化,侧重于航道的运输效率,忽略了船舶进入泊位的作业效率。
在模型求解方面:李平等[12]将遗传算法和混合优化策略应用到了求解集装箱港口的泊位调度问题中;KAP等[13]以船舶因延误离港而导致的罚金与因不合理停泊导致的额外搬运集装箱费用之和最小为目标,提出了一种基于模拟退火算法的泊位分配模型;CHUANG等[14]设计了模糊遗传算法求解航线调度优化模型,可为船舶航线调度问题提供辅助支持。
综上所述,目前关于船舶进出港调度的研究主要侧重于航道容量和泊位分配中的单一方面,在实际的港口调度中,船舶进出港管理效率较低。对此,以航道为切入点,协调泊位资源,构建多目标港口船舶调度优化模型,设计适于求解的多目标遗传算法,并设计模拟数据进行验证。
1 问题描述
船舶调度的目的是在遵循航道管理规则和保证港口水域通航安全的条件下,使船舶尽快、尽量多地通过航道,减少船舶延误。对于单向航道,在港口繁忙的情况下,港口船舶调度的核心问题是泊位和航道资源的优化配置。交通量的大小受船舶进出港初始状态、同向船舶的安排协调、进出流量的安排控制以及泊位冲突消解等因素的制约。因此,港口船舶调度问题是典型的NP-Hard (Non-deterministic Polynomial-time Hard)问题。
2 模型建立
2.1概念解释
1) 单向航道:同一时间只允许同一个方向通航的航道。
2) 时隙分配:这里的一个时隙指从一艘船舶开始进出港到下一艘船舶开始进出港的时间间隔。
3) 流量转换:船舶进港流量和出港流量的协调。
2.2模型假设
1) 港口已做好船舶靠泊作业计划,船舶交通管理中心负责港口船舶进出港调度。
2) 天气对港口船舶调度没有影响,拖船和引航员充足且能准时到位。
2.3船舶调度模型建立
2.3.1目标函数的建立
港口方和船方在船舶调度过程中的利益诉求不同。单纯从时间的维度考虑,港口方希望所有船舶完成调度的时间最短,而船方则希望各自船舶在港的等待时间最短。这里根据两利益方关心的问题,构建多目标目标函数Min[F,W]
(1)
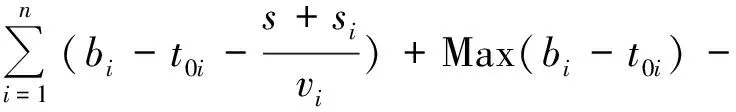
Min(bi-t0i)
(2)
式(1)~式(2)中:F为所有船舶完成进出港的最少总时间;W为修正后所有船舶等候进出港的最少时间总和;bi为第i艘船舶进/出港开始时刻;fi为第i艘船舶进/出港结束时刻;t0i为船舶i进入报告线的时刻;s为报告线与航道入口间的距离;si为理论上第i艘船舶的泊位与航道入口间的距离;vi为理论上第i艘船舶从进入航道到抵达泊位处的平均速度;b0为上一时间段内最后一艘船舶进港(出港)开始时刻;f0为上一时间段内最后一艘船舶进港(出港)结束时刻;h0为本阶段第一艘船舶与上一阶段最后一艘船舶的安全时间间隔。
式(1)表示本阶段所有船舶完成进出港所使用的总时间最少;式(2)表示所有船舶等候进出港时间总和最少。这里的船舶等候进出港时间指船舶实际使用的进出港时间与理论上船舶最快进出港时间的差值,即船舶在港浪费的时间成本。
2.3.2船舶调度模型约束的建立
IOi=(0,1)i=1,2,3,…,n
(3)
Rij=(0,1)i=1,2,3,…,n
(4)
Bij=(0,1)i=1,2,3,…,n
(5)
Berthim=(0,1)i=1,2,3,…,n
(6)
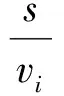
(7)
(bi-b0-h-Bijh1)×[1-(IOi-IO0)2]≥0
i=1,2,3,…,n
(8)
(fi-f0-h-Bijh1)×[1-(IOi-IO0)2]≥0
i=1,2,3,…,n
(9)
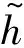
(10)
fi-bi-pi≥0i=1,2,3,…,n
(11)
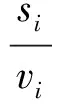
(12)
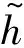
(13)
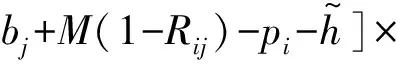
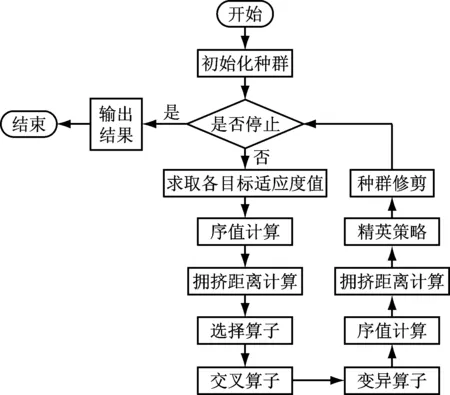
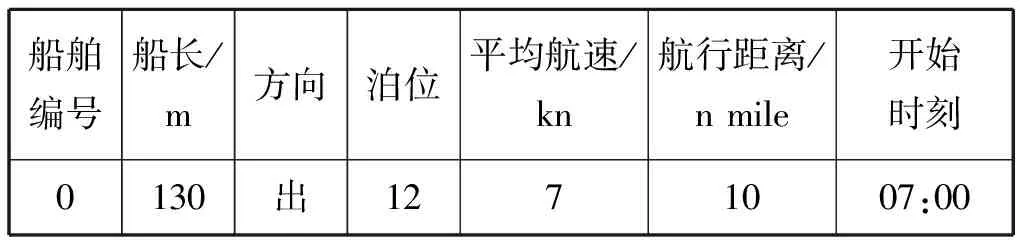
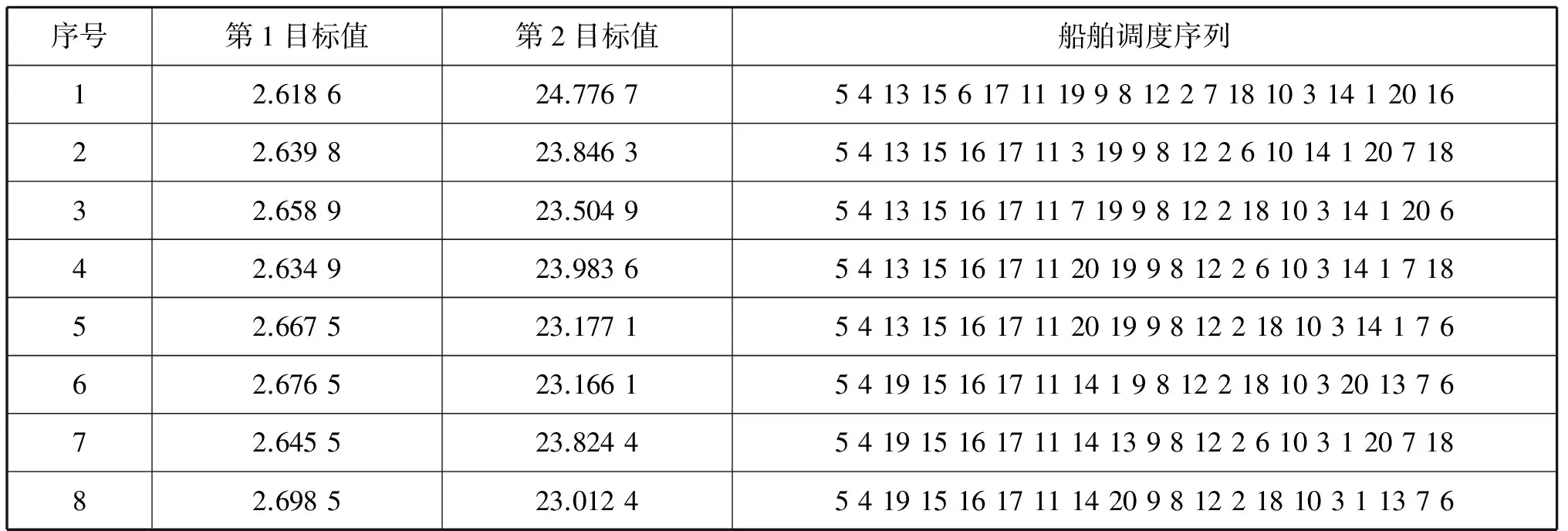
(IOi-IOj)2≥0i (14) (bi-bj+MRij-h-Bijh1)×[1- (IOi-IOj)2]≥0i (15) [-bi+bj+M(1-Rij)-h-Bijh1]×[1- (IOi-IOj)2]≥0i (16) (fi-fj+MRij-h-Bijh1)× [1-(IOi-IOj)2]≥0i (17) [-fi+fj+M(1-Rij)-h-Bijh]×[1- (IOi-IOj)2]≥0i (18) (1-Berthin)+M(1-IOi)>0t=bi (19) 式(7)为船舶i开始调度时刻必须晚于船舶i预计到达航道入口的时间; 式(8)~式(10)为保证模型的连续性构建的初始化约束; 式(11)~式(14)为流量转换约束,主要实现进出港船舶的流量在时间上的转换; 式(15)~式(18)为时隙分配约束,用于协调先后调度的2艘船舶同向航行时的安全问题,主要考虑安全时间间隔、船舶的先后次序和泊位远近;式(19)为泊位冲突消解约束,保证任意一艘进港船舶调度开始时刻,其将要停靠的泊位是空闲的。 遗传算法具有较好的并行计算能力,是在多目标优化领域应用最成功的算法之一。这里针对港口船舶调度设计遗传算法进行求解。为模型设计的多目标遗传算法流程图见图1。 使用MATLAB 2010b设计港口船舶调度多目标遗传算法程序,基于MATLAB GUI实现计算结果的可视化。对某港口某天某时段的船舶进行调度试验,模拟20艘船舶(14进6出)准备时刻的间隔服从λ=20的负指数分布规律的场景。准备时刻是指只要泊位和航道条件允许,即可调度船舶的时刻;航行距离是指航道起点与泊位间的距离。模拟数据的船舶信息见表1。 图1 多目标遗传算法流程图 假设上一阶段最后一艘船舶的进出港开始时刻为07:00。表2给出了上一阶段最后一艘船舶的相关信息。 表2 上一阶段最后一艘船舶信息 泊位是码头集团按照申请预先分配完成的,且泊位的条件都满足要停靠船舶的要求。表3给出了本阶段调度开始时刻泊位的空闲和占用状态,模拟数据假设共有18个泊位。 表3 泊位开始时刻的空闲和占用状态 将上述数据读入程序进行运算,参数为:种群大小200,代沟0.9,交叉概率0.95,变异概率0.05,最大遗传代数200。运行结果见图2。可看出共有8个Pareto最优解,20艘船舶调度完成所用总时间为2.618 6 h,添加惩罚后的总等待时间为23.012 4 h;种群在不断寻优,并在200代以内收敛。 8个Pareto最优解见表4。在总调度时间的方向上,最优解为2.618 6 h,此时总等待时间的适应度值为24.776 7 h。在总等待时间方向上,最优解为23.012 4 h,此时总调度时间为2.698 5 h。这符合多目标遗传算法结果的特点:当一个目标改进时,另一个目标会相应地衰退。由于船舶准备调度时刻比较集中,因此虽然能增加船舶可调度时间段,但同时也会造成船舶等待时间延长。 对于单向航道,航道上的船舶不能对遇,在进行流量转换前必须保证航道上没有船舶,进而会消耗较多的时间。因此,理论上对于较长的单向航道而言,流量转换的次数越少,所有船舶完成调度所用时间就越短。8个Pareto最优解的调度方案都只进行3次流量转换,大大提高了船舶的调度效率。 每个Pareto最优解代表一个调度方案,经检验,8个Pareto最优解均符合以上约束,可保证船舶的安全。在实际应用中,若港口追求总调度时间最短,可选用第1目标值较小的调度方案Pareto1;若兼顾每艘船舶的等待时间,可选用第2目标值较小的调度方案Pareto8。 表4 Pareto 最优解 研究了基于单向航道和泊位资源协调调度的船舶交通管理问题,建立了以所有船舶总在港时间和等待时间最少为目标的基于单向航道的多目标船舶调度优化模型。使用MATLAB 2010b编写了港口船舶调度多程序,基于MATLAB GUI实现了计算结果的可视化。经验证,该模型能大大提高船舶进出港作业的效率。 [1] 邵俊岗, 许小兵,王煜,等. 洋山港区运营阶段的港口通过能力[J]. 上海海事大学学报, 2008, 29(4): 25-28. [2] 李子强. 基于交通流分析的航道通过能力研究[J]. 山东交通学院学报,2009,17(4):32-35. [3] 代君, 王当利, 刘克中. 基于船舶领域模型的港口受限航道通过能力计算方法[J]. 武汉理工大学学报:交通科学与工程版, 2009, 33(4): 679-682. [4] 张玮, 廖鹏,吴玲莉,等. 船闸通过能力主要影响因素[J].交通运输工程学报, 2004, 4(3): 108-110. [5] 胡洋. 三峡工程五级船闸通过能力初步分析和提高枢纽综合通过能力的对策[J]. 水运工程, 2004(10): 74-77. [6] 王小平, 齐欢, 肖恒辉, 等. 基于串联排队网络的三峡葛洲坝水利枢纽联合调度模型[J].交通运输工程学报, 2006, 6(3): 82-86. [7] 徐国裕, 郭涂城, 吴兆麟. 单向水道船舶进出港最佳排序模式[J]. 大连海事大学学报, 2008, 34(4):150-153. [8] LLOYD D N.Integrating VTS with Port Operation[Z]. Hongkong: Proceedings of VTS 2004,2004: 44-52. [9] MEINE J,KRAMER M.Creation of a Regionee VTS with Data Fusion and Integration of Vessel Data and Movement Details Over the Area of Several Independent Ports, Coastal And Inland Waterways[Z]. Hongkong: Proceedings of VTS 2004,2004: 235-248. [10] OZGECAN S U T. Performance Modeling and Risk Analysis of Transit Vessel Traffic in the Istanbul Strait: Studies on Queues with Multiple Types of Interruptions [D]. New Brunswick: Rutgers the State University of New Jersey, 2011. [11] PULUGURTHAL S S, NAMBISAN S S. Using Genetic Algorithms to Evaluate Aircraft Ground Holding Policy Under Static Conditions[J]. Journal of Transportation Engineering, 2011,127(5): 433-441. [12] 李平, 孙俊清, 韩梅 .泊位调度问题的GATS混合优化策略[J] .天津理工大学学报, 2009, 22(4): 58-61. [13] KAP H K, KYUNG C. Moon Beth Scheduling by Simulated Annealing[J]. Transportation Research Part B, 2012(37): 541-560. [14] CHUANG T N, LIN C T, KUNG J Y,etal. Planning the Route of Container Vessels: A Fuzzy Genetic Approach[J]. Expert Systems with Applications, 2010(37): 2948-2956. OptimizationofVesselSchedulingBasedonCoordinationofOne-WayChannelandBerths ZHANGXinyu1,2,GUOZijian2,WANGJintao1,LINJun1 Careful coordinating the channel and berths can maximize the efficiency of a port. With the objective that total sum of time of all vessels spending in the harbor and waiting for available channel is minimized, a multi-objective optimization model of vessel scheduling based on one-way channel is built. Initialization constraints, traffic conversion constraints, slot allocation constraints and berths conflict resolution models are defined respectively based on traffic flow characteristics in different regions of the port. A multi-objective genetic algorithm is designed to solve the proposed model, and a practical scenario of 20 vessels at a peak period is designed to validate the reasonability and effectiveness of the model. The simulation results show that there are 8 Pareto optimal scheduling scheme options as the optimal solution, in which the total of time is 2.6186 hours and the waiting time is 23.0124 hours. The results of experiment suggest that the proposed scheduling model is of great value to improve the efficiency of vessel traffic. waterway transportation; one-way channel; vessel scheduling optimization; multi-objective genetic algorithm; slot allocation; traffic flow transition 2015-05-11 国家自然科学基金(51309043);中央高校基本科研业务费专项资金(3132014202); 交通部应用基础研究项目(2014329225020);中国博士后科学基金(2014M551095);辽宁省自然科学基金(2014025005);辽宁省高校杰出青年学者成长计划(LJQ2014052) 张新宇(1978—),男,吉林长春人,副教授,博士生,主要研究方向为交通信息工程及控制。E-mail:41544391@qq.com 1000-4653(2015)03-0033-04 U691+.3 A3 算法设计
4 实例验证

5 结束语
(1. Key Laboratory of Maritime Dynamic Simulation and Control of Ministry of Transportation, Dalian Maritime University, Dalian 116026, China; 2. School of Hydraulic Engineering, Dalian University of Technology, Dalian 116023, China)
