基于自适应α－β滤波的HFSWR海上目标航迹跟踪

孙伟峰，纪永刚，张晓莹，2，于长军，戴永寿

（1.中国石油大学（华东）信息与控制工程学院，山东 青岛266580；2.国家海洋局 第一海洋研究所，山东 青岛266061；3.哈尔滨工业大学（威海）信息与电气工程学院，山东 威海264209）

高频地波雷达（High Frequency Surface Wave Radar，HFSWR）具有超视距探测能力，且能够全天候工作，已成为海上目标探测的重要手段［1］。高频地波雷达用于海上目标监测时，探测性能会受到海杂波、电离层干扰等外部噪声和雷达系统内部噪声的影响，导致单时刻目标点迹探测虚警率较高。航迹跟踪是利用多时刻目标点迹探测结果，根据目标运动规律得到目标的运动轨迹，从而实现海面目标的连续监测。对海上目标航迹进行实时跟踪，既可以剔除目标检测时出现的虚假目标，又可以提高目标在距离向和方位向的探测精度，总体上提高对海上目标整体的监视监测性能。

α－β滤波是一种典型的高频地波雷达目标航迹跟踪算法，在德国WERA雷达的目标跟踪系统中得到了应用，通过与AIS航迹的对比表明，该方法能够得到符合需求的目标航迹［1－2］。WERA雷达采用的α－β滤波方法中系数为恒定设置，由于不同地波雷达实测数据的特点不同，其系数设置不能直接应用于其他雷达系统；并且，恒定系数滤波方法主要适用于严格非机动目标，而实际目标运动情况复杂多样，采用恒定系数滤波方法跟踪机动目标时，会出现跟踪误差，且目标的机动性越大其航迹跟踪误差就越大，甚至会出现无法跟踪目标航迹的情形。目前，已有一些自适应α－β滤波算法的研究工作［3－5］，但这些研究主要是针对常规微波雷达的目标航迹跟踪问题，且大都只是开展了仿真实验，没有探讨在实测数据处理时的适用性。

本文针对实际高频地波雷达海上运动目标的航迹跟踪问题，给出了极坐标下的目标运动模型，分析了α－β滤波算法应用于地波雷达航迹跟踪时的参数选取问题，在此基础上提出了适用于高频地波雷达航迹跟踪的自适应α－β滤波系数选取方法。利用仿真及实测地波雷达目标点迹数据，采用本文提出的方法与已有自适应滤波方法开展目标航迹跟踪实验，以AIS（Automatic Identification System）航迹作为参考基准，对方法的适用性及有效性进行了对比分析。

1 自适应α－β滤波方法

1.1 模型建立

高频地波雷达目标运动模型的建立是α－β滤波航迹跟踪的关键问题之一。高频地波雷达在以雷达波束为中心的极坐标下获取目标量测，如果采用笛卡尔坐标系建立目标的运动模型，在跟踪滤波过程中就需要进行坐标转换，这势必会引入转换误差；同时，坐标转换过程受方位角影响，而目标量测数据中角度量测的误差较大，这将进一步增大转换误差。因此，本文在极坐标系下建立目标运动模型：

式中，R（k），˙R（k）分别为k时刻的径向距离和径向速度；θ（k），˙θ（k）分别为k时刻的方位角与方位角速度；T为积累时间。在该模型下，径向距离与方位角是解耦的。

由式（1）的运动模型可知预测方程：

式中，下标p，s分别表示预测和滤波。

高频地波雷达目标探测数据提供了目标的径向距离、径向速度和方位角等信息，本文直接采用径向速度量测建立速度滤波方程，得到高频地波雷达的α－β滤波平滑方程：

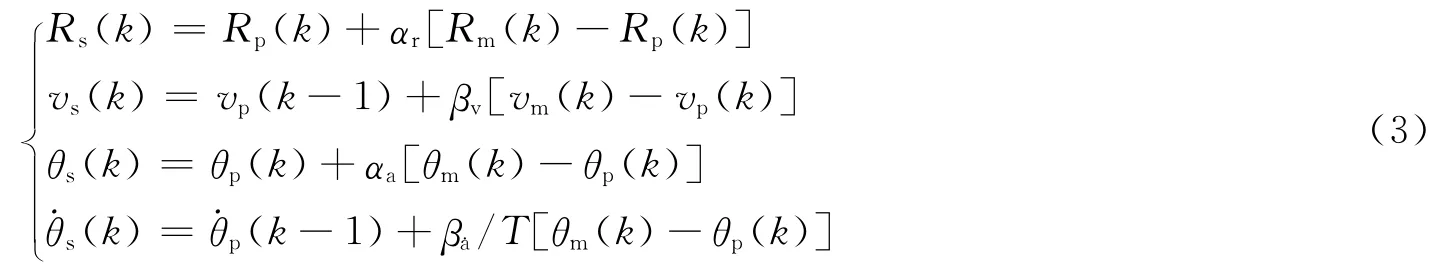
式中，下标p，s，m 分别表示预测、滤波和量测；参数v（k）表示k时刻的径向速度；αr，αa，βv及β˙a分别表示α－β滤波方法中径向距离、方位角的α滤波参数以及径向速度、方位角速度的β滤波参数。

1.2 自适应系数选取

α－β滤波系数的选取是模型确立之后的另一个关键问题，由式（3）可以看出，α，β参数为目标量测值与预测值之间偏差的加权系数，它们的设置需要依据高频地波雷达各个量测参量的测量精度而定，其设置的合理与否将直接影响高频地波雷达航迹跟踪性能。

WERA 雷达采用恒定系数选取方法［6－8］，α，β系数按照Benedict最优准则β＝α2／（2－α）［9］得到。实际高频地波雷达航迹跟踪应用中，需要根据实测数据的特点寻找比较理想的系数值，以得到较高的航迹跟踪性能。若能够按照一定的准则或模型实现高频地波雷达目标航迹跟踪中滤波系数的自适应选取，在处理不同数据时模型可自适应地确定滤波系数的最优值，不需要经过多次试验来求取。

图1 雷达量测优先级Fig.1 Priority of HFSWR measurements

高频地波雷达用于海上目标监视监测时采用较长的积累时间，可得到较高的多普勒分辨率，即相对于目标测距和测向，目标径向速度量测是最为准确的，如图1所示。据此，我们首先确定滤波方程中径向速度的滤波系数β，然后根据Benedict最优关系［9］来确定径向距离滤波系数。

由公式（3）可知，β可以看作速度新息对预测值的修正系数，其值的大小反映预测值与量测值之间的偏差对预测值的修正程度。新息变大说明预测值与量测值之间偏差增大，需要增大滤波系数；新息变小说明预测值与量测值比较接近，需要相应地减小滤波系数，从而实现稳定地航迹滤波跟踪。此外，根据Benedict最优关系式［9］可知β取值为0～1，并且新息增大时修正系数β也要相应增大，当测量误差很大时，β应快速收敛到1。

根据上述分析，对滤波系数β建立如下的函数模型：

式中，σv为径向速度的测量误差。由于新息｜vm（k）－vp（k）｜的取值在［0，∞）之间，该函数模型中βv的取值在［0，1］之间。结合α的取值区间，可得：

式中，k为航迹号；｜vm（k）－vp（k）｜为第k条航迹径向速度预测值与量测值之差的绝对值。

在方位角和方位角速度滤波模型中［10］，方位角是直接测量数据，对于方位角滤波系数，先利用角度关联阈值确定角度滤波系数αa：

式中，σa为角度的测量误差；｜θm（k）－θp（k）｜为第k条航迹角度预测值与量测值之差的绝对值。同样地，利用角度滤波系数可以求得β˙a（k）。

2 仿真实验

为了与实际地波雷达量测特点一致，本文根据实际雷达站的位置，在极坐标下仿真了雷达扫描扇形区域内的杂波和淹没在杂波中的5个船只目标，如图2所示。

图2 HFSWR目标与杂波仿真点迹分布图Fig.2 Simulatedpoints distribution for HFSWR targets and clutter

5个目标的位置及运动参数如表1所示，其中距离和角度参数均是以雷达站为基准，角度是指目标与雷达站连线与雷达扫描中心轴的夹角，顺时针为正。

表1 5个仿真目标的参数Table 1 Parameters of the five simulated targets

利用上述仿真数据，采用本文方法即公式（4）～（6）进行目标跟踪仿真实验，并与以下2种方法进行对比。

方法1：王红亮等［4］提出的自适应系数方法：

式中，表示第k次迭代预测误差的方差为雷达测量误差的方差。β的值由Benedict最优准则确定。

方法2：工程常用的实时系数确定方法［4］：

与方法1不同，本文方法利用高频地波雷达目标量测参数的特点，首先由测量精度高的径向速度参数确定β的值，再由最优准则确定α参数。

分别采用3种方法进行航迹跟踪实验，得到的航迹结果分别示于图3a至图3c中。图中数字表示目标的序号，其标注位置为航迹起始点。若数字标注在航迹起始点，则表示该航迹从刚开始就被跟踪到；若数字标注在航迹中间，则表明该航迹在航迹开始阶段没有被跟踪到。

由图3中的跟踪结果可以看出，3种方法都能够跟踪到5个目标，方法1和本文方法能够对5条航迹进行长时间跟踪，而方法2只能跟踪到目标5的部分航迹。

利用漏跟踪率指标对3种方法的航迹跟踪性能进行评价，将其定义为多次跟踪实验中，不能正确跟踪目标的次数占总跟踪次数的比率。利用3种方法分别进行200次仿真实验，得到的漏跟踪率统计结果见表2，可见，对于目标5，方法2的漏跟踪率达到了77%，而方法1与本文方法的漏跟踪率仅为1%。

由于方法2的跟踪效果较差，以下我们仅对方法1和本文方法的航迹跟踪性能进行比较。以目标5的跟踪为例，将2种方法的航迹跟踪结果示于图4中。由图4可以看出，本文方法与方法1都起到了滤除噪声、平滑航迹的效果。

为了更加详细地比较2种方法的航迹跟踪性能，对二者航迹跟踪的径向速度、径向距离以及方位角误差进行比较，其具体统计结果见图5及表3。

由图5及表3中的结果对比可知，二者获取的航迹参数中，径向速度没有较大差别，对于径向距离和方位角，本文方法取得了较高的跟踪精度。由航迹跟踪率和跟踪精度的比较分析可知，本文提出的方法能够得到更好的航迹跟踪性能，不论在航迹长度还是航迹误差方面都略胜一筹，方法2的跟踪效果较差，方法1的效果处于两者之间。

图5 2种方法的误差曲线Fig.5 Error curves of the two methods

表3 跟踪误差统计Table 3Tracking error statistics

将目标跟踪算法应用于实际的船只目标航迹跟踪是研究各种地波雷达航迹跟踪算法的最终目标，一个算法的提出或改进要具有实际的工程应用价值才具有真正的研究意义。以上针对实际工程应用提出了一种改进算法，下面我们利用高频地波雷达实测数据对改进的算法进行验证，并对船只目标航迹跟踪的结果进行评价。

3 实测数据分析与验证

3.1 航迹跟踪整体分析

本文采用的实测高频地波雷达数据源于威海地波雷达站，雷达工作频率为4.7MHz。采用第2节中的方法1和本文方法开展航迹跟踪实验，并基于实测同步AIS数据对两种算法的跟踪性能进行评价。本文方法与方法1得到的目标航迹跟踪结果分别见图6和图7。

由图6和图7可见，本文方法得到的航迹数量明显多于方法1的跟踪结果。在图中标出的3个区域中，图6中区域1的航迹明显多于图7中相同区域的航迹；在区域2中的一些航迹，采用恒定系统的算法没有跟踪到，而本文方法的航迹结果中对其进行了成功跟踪，且该航迹没有对应的AIS信息，有可能是非合作船只目标，这对于监测非合作目标，维护海上安全与秩序具有重要意义。

图6 本文方法HFSWR航迹跟踪结果Fig.6 HFSWR track of the proposed method

图7 方法1HFSWR航迹跟踪结果Fig.7 HFSWR track of method one

海面船只的运动一般情况下短时间内不会出现较大程度的机动，反映在航迹中即不会出现剧烈的抖动，可以利用目标航迹的平滑性衡量航迹跟踪方法的性能优劣。分别选取图6、图7中区域3中的部分航迹进行分析，如图8所示。

由图8可见，本文方法的航迹跟踪结果（图8a）比方法1的航迹跟踪结果（图8b）要平滑，方法1的航迹结果波动较为剧烈。与对应的AIS航迹对比可以看出，对于航迹1，利用本文方法得到的航迹明显比与利用方法1得到的航迹持续时间长。

图8 图6和图7中区域3中的部分航迹Fig.8 Part oftracking results withinarea3in Fig.6and Fig.7

为了进一步比较两种航迹跟踪算法的跟踪性能，对航迹跟踪结果中不同长度段的航迹数目、航迹平均长度进行统计，结果见表4。由表4可以看出，采用本文方法得到的航迹结果在不同长度段数目都比方法1多，且航迹平均长度较长。

表4 2种方法航迹参数统计Table 4 Track parameter statistics of the two methods

通过上述对航迹结果的整体覆盖范围和航迹长度的统计分析可知，采用本文方法对高频地波雷达船只目标航迹进行跟踪得到的航迹跟踪范围更远、航迹数目更多（跟踪率更高）、航迹平滑性更好，验证了提出方法的有效性。

3.2 航迹跟踪个例分析

为了进一步分析对实测数据的航迹跟踪精度，选取航迹个例对跟踪结果进行定量评价。选取目标个例的详细信息见表5。

表5 航迹个例详细信息Table 5 Information of a selected track

目标个例的航迹跟踪结果如图9所示，可见，两种方法能够得到相近的跟踪效果，本文方法的航迹结果比方法1得到的航迹结果更加平滑。

为了比较2种方法的航迹跟踪精度，分别将其航迹结果与同步AIS航迹信息进行对比。由于AIS的采样间隔不定，且测量坐标与地波雷达不同，因此，首先将二者进行时间与空间配准，然后将同步AIS信息用于HFSWR航迹结果的评价，分别对其径向速度、径向距离和方位角测量误差进行对比，如图10所示，相应的跟踪误差统计列于表6中。

由图10及表6可知，2种方法得到的航迹中径向速度、径向距离及方位角跟踪误差的最大值分别在0.7km／h，1.25km，3.1°以内。与方法1相比，本文方法的跟踪误差及误差变化更小。其中，径向速度误差与径向距离误差相近，方位角误差平均可以减小0.14°，且误差波动更趋平稳，跟踪精度更高。

表6 跟踪误差统计Table 6 Tracking error statistics

4 结论

本文针对高频地波雷达海上目标的航迹跟踪问题，结合滤波系数的物理含义，对基于α－β滤波的航迹跟踪方法中滤波系数的自适应选取方法进行了研究，充分利用高频地波雷达实测数据中径向速度测量精度较高的特点确定优先级，进行滤波系数的自适应选取，提出了一种适用于高频地波雷达航迹跟踪的α－β滤波自适应系数选取方法。仿真及实测数据航迹跟踪实验结果均表明，本文提出的自适应α－β滤波算法能够得到更高的航迹跟踪精度，输出的航迹更加平滑，且跟踪丢失率低。

（References）：

［1］GURGEL K W，SCHLICK T，HORSTMANN J，et al.Evaluation of an HF－radar ship detection and tracking algorithm by comparison to AIS and SAR data［C］∥IEEE，Waterside security conference（WSS）.Carrara：IEEE，2010：1－6.

［2］DZVONKOVSKAYA A，ROHLING H.HF radar performance analysis based on AIS ship information［C］∥IEEE，Radar conference.Washington：IEEE，2010：1239－1244.

［3］XU L P.An adaptiveα－βfilter algorithm for tracking the maneuvering target［J］.Journal of Xidian University，1998，25（3）：314－317.许录平.跟踪机动目标的自适应α－β滤波算法［J］.西安电子科技大学学报，1998，25（3）：314－317.

［4］WANG H L，LI F，ZHAO Y G.An adaptiveα－βalgorithm filter for maneuvering target tracking［J］.Science and Technology of Radar，2007，5（4）：278－291.王红亮，李枫，赵亦工.一种机动目标跟踪的自适应α－β滤波算法［J］.雷达科学与技术，2007，5（4）：278－291.

［5］MA L.Research on Track－While－Scan radar tracking algorithm［D］.Xi＇an：Northwestern Polytechnical University，2004：6－11.马玲.边扫描边跟踪雷达航迹跟踪算法的研究［D］.西安：西北工业大学，2004：6－11.

［6］DZVONKOVSKAYA A，ROHLING H.HF radar ship detection and tracking using WERA system［C］∥IET，International conference on radar systems.Edinburgh：IET，2007：1－5.

［7］DZVONKOVSKAYA A，GURGEL K－W，ROHLING H，et al.Low power high frequency surface wave radar application for ship detection and tracking［C］∥IEEE，International Conference on Radar（RADAR）.Adelaide：IEEE，2008：627－632.

［8］DZVONKOVSKAYA A，GURGEL K－W，ROHLING H，et al.HF radar WERA application for ship detection and tracking［J］.European Journal of Navigation，2009，7（3）：18－25.

［9］KALATA P R.The tracking index：ageneralized parameter forα－βandα－β－γtarget trackers［J］.IEEE Transactions on Aerospace and Electronic Systems，1984，AES－20（2）：174－182.

［10］XIA J T，REN Z，CHEN L，et al.A Kalman Filtering Algorithm in polar coordinates［J］.Journal of Northwestern Polytechnical University，2000，18（3）：396－399.夏建涛，任震，陈立，等.极坐标下卡尔曼滤波算法研究［J］.西北工业大学学报，2000，18（3）：396－399.