芬迪湾、缅因湾和圣劳伦斯湾潮汐共振的数值研究＊

崔欣梅，方国洪＊，滕 飞，吴 頔

（1.中国科学院 南海海洋研究所，广东 广州510301；2.中国科学院大学 热带海洋环境国家重点实验室，广东 广州510301；3.中国科学院大学，北京100039；4.国家海洋局 第一海洋研究所，山东 青岛266061；5.中国海洋大学 海洋环境学院，山东 青岛266100）

共振是自然界普遍存在的现象，在力学、声学、电磁学、光学、原子物理学等学科及其相关的工程技术问题中都会遇到共振的问题。对于海洋潮汐，共振现象亦大量存在。共振导致的大振幅潮汐，也就消耗了大量潮汐能量，而消耗的潮汐能量必须由日－地－月系统中动能和势能来提供，从而导致月球公转的减速和地球自转的减速，后者又导致日长的变长。芬迪湾存在全球潮差最大的半日潮，在芬迪湾顶部的米纳斯湾曾出现15m多的潮高。虽然半日潮S2分潮（12.00h），N2分潮（12.66h）也较强，但主要以 M2分潮（12.42h）为主。芬迪湾的潮汐现象一直备受海洋学家的关注，早在19世纪末Lamb［1］就对芬迪湾较强的半日潮进行了研究，开启了关于海洋潮汐共振研究的序幕。早期关于芬迪湾潮汐共振的研究主要是根据四分之一波长共振理论，对于半封闭矩形海区，当海区长度等于入射波波长的四分之一时会产生共振，根据波长、周期和波速的关系可估算出海区的共振周期，即 Merian公式（Proudman，1953［2］）。Proudman［2］和 Honda等［3］和认为芬迪湾较强的半日潮与潮波共振有关，芬迪湾的长度约等于半日潮波波长的四分之一，粗略估算了芬迪湾的共振周期约11.09h，较接近半日潮的周期。然而Rao［4］按照Merian公式计算得到的芬迪湾共振周期为9.047 h；Duff［5］认为缅因湾和芬迪湾应作为一个系统进行研究，不能将二者割裂开来。Garrett［6］将缅因湾和芬迪湾作为一个系统进行研究，首次考虑了摩擦的作用，根据实际观测水位计算了缅因－芬迪湾系统的共振周期（13.3h）和能量耗散因子 Q（3.1～5.6）。Garrett［7］采用Platzman［8］简正模态方法计算芬迪湾的共振周期时，选择了多个位置不同的开边界，所得的共振周期也不相同，介于12.38～12.98h。Ku等［9］考虑了半日潮每18.6年的调制作用对摩擦的影响，从观测数据、数值模式和理论分析三方面分析，认为芬迪湾的共振周期应该为13.5～13.7h。然而Godin［10－11］对此持有不同看法，同样在考虑半日潮调制作用的情况下，根据观测数据和数值计算的结果分析认为共振周期应为12.5～12.7h。由此可见，对于芬迪湾的共振周期目前还存在不同看法。本文采用我们设计的“初值方法”，对芬迪湾和缅因湾的共振周期进行估算，结果表明，其值为13h，大约等于 Garrett［6］和 Godin［10－11］估计值的中数。Godin［11］还指出，圣劳伦斯湾不发生潮汐共振，由于该海湾位于缅因－芬迪湾附近，我们对它的共振周期也一并进行了估算。

1 数值方法

早先海洋学家均采用由极大简化了的海域形状和地形所得的共振周期公式来估算潮汐共振周期（Proudman［2］；Defant［12］）。随着计算机技术的发展，Platzman［8］采用数值方法计算海区的共振周期，提出简正模态方法，此种方法编程极为复杂，且对开边界位置的选择有较大主观性。Webb［13］提出采用边值方法计算海区的共振周期，在开边界处给一个频率的波，采用数值方法计算海区对这一频率的响应情况。为了找出共振频率，必须对许多不同频率计算海区对各个频率的响应情况进行计算，然后得出水位振幅随频率的变化曲线。这种方法操作较麻烦，较花费时间。到目前为止，国内外关于潮汐共振的数值研究主要基于简正模态方法和边值方法。本文采用一种不同的方法，我们称之为“初值方法”。这种方法简单，计算量也较小，可同时计算任意多频率，用傅里叶变换法对数值模式计算得到的水位数据进行频谱分析，数值模式计算由任意频率叠加生成的开边界水位驱动，故称之为“初值方法”。其基本原理和操作方法如下。

1.1 数值模式

我们所采用的数值模式是在POM（Princeton Ocean Model）模式基础上修改得到的。目前关于潮汐共振的研究还是在二维、线性框架下进行的，故动力学方程取为：

式中，t表示时间；λ和φ分别代表经度和纬度；ζ表示水位大小；u和v分别表示流速向东和向北分量；R表示地球半径；f＝2Ωsinφ，代表科氏参数；Ω表示地球旋转的角速度；Η表示水深；r表示线性化之后的底摩擦系数。

1.2 开边界驱动

模型主要靠开边界水位驱动。为了计算海区对各频率潮波的响应情况，开边界条件为：

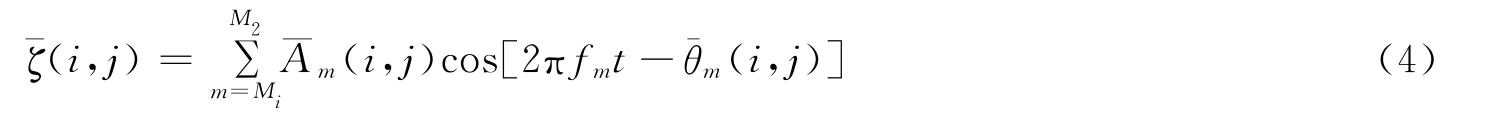
式中，i，j表示开边界处的网格点；fm≡mΔf表示第m个频率Δf代表谱的分辨率，m＝M1，M1＋1，…，M2；分别表示第m个频率的振幅和迟角。我们研究的目的是想知道研究海区对来自深海大洋潮波的响应情况，因此Δf的选择需要小于主要分潮频率间之差。Q1，O1，K1，N2，M2和S2分潮的频率分别是0.037 22，0.038 73，0.041 78，0.079 00，0.080 51和0.083 33h－1，最小的频率差约为0.001 51h－1，我们选择Δf＝1/1 024h－1，小于0.001 51h－1。其中分母之所以选择1 024是因为1 024＝210，这使得对结果进行Fourier变换时可以采用快速Fourier变换（FFT），以节省计算时间。如果采用较小或者较大的频率分辨率Δf，则模式积分的时间也要随之采用更长或更短的时间长度。

1.3 计算区域和模式设置

计算海区取（82°～0°W，6°～58°N），覆盖了北大西洋大部（图1）。网格分辨率为（1/12°×1/12°），水深取自Etopo1水深数据，取底摩擦系数为0.001m/s。开边界处的振幅均取常数，即；迟角与开边界位置（i，j）无关，但与频率有关，不同频率的迟角不同，即是通过随机数生成器计算得到的一组位于（0，2π）之间的随机数，选择随机迟角是为了避免在某一时刻出现特别高或特别低的水位。我们在计算中取M1和M2分别为1和171，所以频率变化区间为1/1 024～171/1 024h－1，即0.023 4～4.007 8 h－1，对应的周期则为6～1 024h（约0.25～43d），覆盖了主要分潮的频率区间。

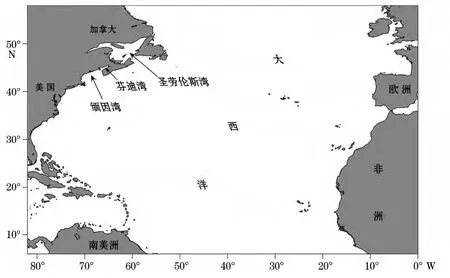
图1 数值模式计算海区范围Fig.1 The domain of the numerical model

图2 缅因湾、芬迪湾和圣劳伦斯湾附近的水深等值线图（m）Fig.2 The water depth contours distribution near the Gulf of Maine，the Bay of Fundy and the Gulf of Saint Lawrence（m）

从图2可以看出，缅因湾和芬迪湾相通，可作为一个系统研究。自大洋至近岸水深变化极为剧烈，梯度较大，由几千米迅速减小到百米，陆架比较狭窄。

模型从静止状态（初始时刻水位和流速均为零）开始积分，时间步长取8s。每计算450步（时间间隔1h）存储一次各计算点的水位，共计算3 072h的数据，取最后1 024h的水位数据，采用Fourier变换进行分析。各网格点的振幅与迟角变化如下：

Munk和Cartwright［14］称Rexp（－iΨ）的值为导纳，Rm（i，j）代表第m个波频在点（i，j）对于边界振幅的响应因子，Sutherland等［15］和Roos等［16］称R和Ψ分别为振幅增益和相变。

2 结果和讨论

我们共研究了3个海区对潮波的响应情况，分别是芬迪湾、缅因湾和圣劳伦斯湾，并把芬迪湾和缅因湾作为一个系统进行了分析（图3）。平均水深指位于海区内的所有网格点水深平均值（表1）。对于某一个波频，本文采用了两种振幅增益分析海区的响应情况，一种是采用海区振幅增益位于前10%的点的值代表整个海区对不同频率的响应情况，另一种是采用整个海区所有点的振幅增益平均值代表整个海区对不同频率的响应情况。采用第二种情况主要是由于缅因湾－芬迪湾和圣劳伦斯湾岸线长且形状多变，若只取振幅增益的前10%点代表整个海区，可能这10%的点集中位于海湾的某一个部分，而并非真的位于海湾的顶部。例如，只统计圣劳伦斯湾振幅增益的前10%计算点，在频率2.60d－1会出现响应峰值，这10%的点几乎全部位于圣劳伦斯湾东北部与大西洋连接的海峡，这并不能代表整个海区的响应情况；而对整个海区的振幅增益做平均则会发现在频率2.60d－1处，振幅增益的响应情况并不十分明显。从图3中可以看出各海区的响应函数情况，在表1中列出了不同海区响应函数的峰值。

表1 各海区平均水深及响应峰值对应的周期（T）和频率（f）Table 1 Mean water depth and peak response frequencies with corresponding periods

从图3a可以看出，缅因－芬迪湾系统响应函数最大峰值的频率约为1.85d－1，即周期为13.0h，此频率为缅因－芬迪湾系统第一模态的共振频率。缅因湾位于大西洋的大陆架上，平均水深约为129m。若假设陆坡的下限为1 500m（图4），陆坡宽度仅为18km，地形的急剧变化导致了能量在陆架上的聚集。在图4中，陆架宽度约为390km，陆架平均水深约为120m，根据四分之一波长理论计算，共振周期约为12.6h，这同模式计算的结果13.0h较为接近。本文的计算结果介于 Garrett［6］和Godin［10－11］的结果之间，可能会更合理。图5为频率（周期）1.85d－1（13.0h）对应的振幅增益和相变大面图。

图3 各海区响应函数（振幅增益关于频率的函数）变化情况Fig.3 Response function（amplitude gains as function of frequency）for various sea areas

图4 缅因湾至大西洋水深剖面图Fig.4 The depth profile map from the Gulf of Maine to the Atlantic

缅因－芬迪湾系统响应函数次最大峰值的频率（周期）为2.60d－1（9.2h）。由图3a，3b和3c三图可以看出，频率（周期）2.60d－1（9.2h）的峰值对应的海区主要是芬迪湾，其振幅增益与频率（周期）1.85d－1（13.0 h）的值比较接近，可见，在此频率芬迪湾产生了较强的响应。芬迪湾长度约为240km，平均水深约84m（表1），根据，这同模式计算结果非常接近。另外，芬迪湾在频率（周期）2.84d－1（8.5h）和3d－1（8.0h）均出现了响应峰值，相对其他两个频率响应峰值偏小。图6和图7分别为频率（周期）2.84 d－1（8.5h）和3d－1（8.0h）的振幅增益和相变大面图。

图5 频率（周期）1.85d－1（13.0h）对应的振幅增益和相变空间分布图Fig.5 The spatial distributions of the amplitude gain and phase change for the frequency（period）of 1.85d－1（13.0h）

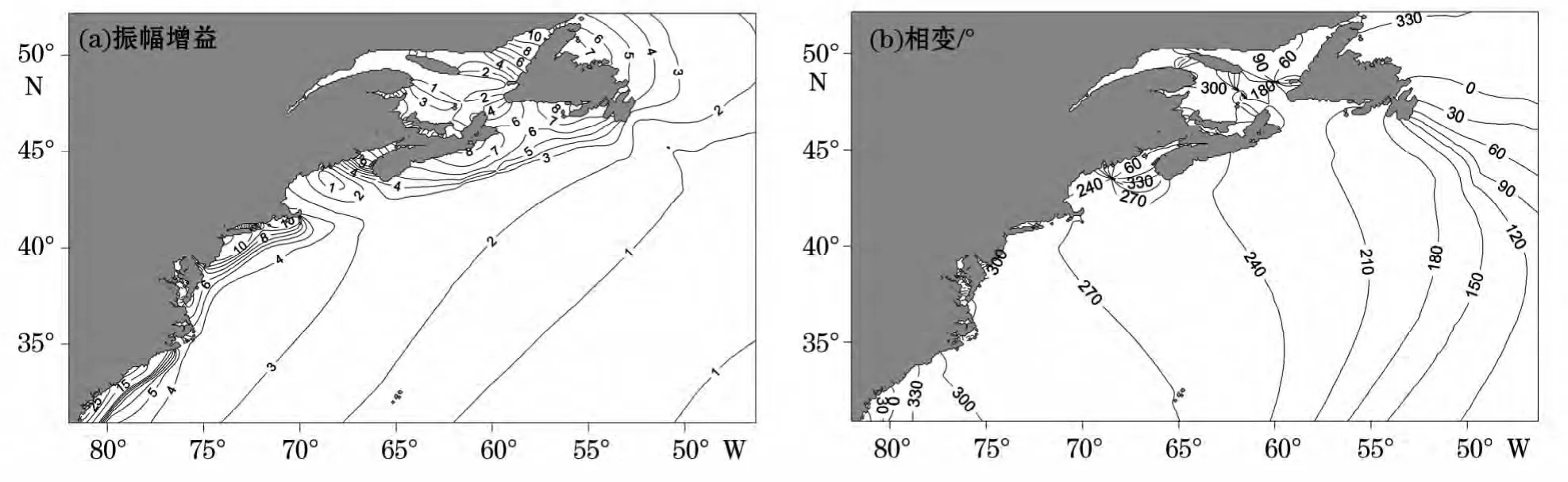
图6 频率（周期）2.84d－1（8.5h）对应的振幅增益和相变空间分布图Fig.6 The spatial distributions of the amplitude gain and phase change for the frequency（period）of 2.84d－1（8.5h）

图7 频率（周期）3d－1（8h）对应的振幅增益和相变空间分布图Fig.7 The spatial distributions of the amplitude gain and phase change for the frequency（period）of 3d－1（8h）

根据振幅增益位于前10%的统计情况（图3d）可以看出，圣劳伦斯湾在频率（周期）2.60d－1（9.2h）也产生了较强的响应，而振幅增益位于前10%的点几乎全部位于圣劳伦斯湾东北部与大西洋连接的狭长海峡（图6a）；对整个海区全部点振幅增益求平均（图3d），可以看出在频率（周期）2.60d－1（9.2h）的响应特征并不十分明显。东北部狭长海峡长度约为570km，平均水深约为130m，根据半波长理论计算共振周期约为8.9h，这同模式计算的结果十分接近。另外，在频率（周期）3.16d－1（7.6h）也存在明显的响应峰值，主要是受来自纽芬兰岛北部海湾波动的影响。图8和图9分别为频率（周期）2.60d－1（9.2h）和3.16d－1（7.6h）对应的振幅增益和相变大面图。

图8 频率（周期）2.60d－1（9.2h）对应的振幅增益和相变空间分布图Fig.8 The spatial distributions of the amplitude gain and phase change for the frequency（period）of 2.60d－1（9.2h）

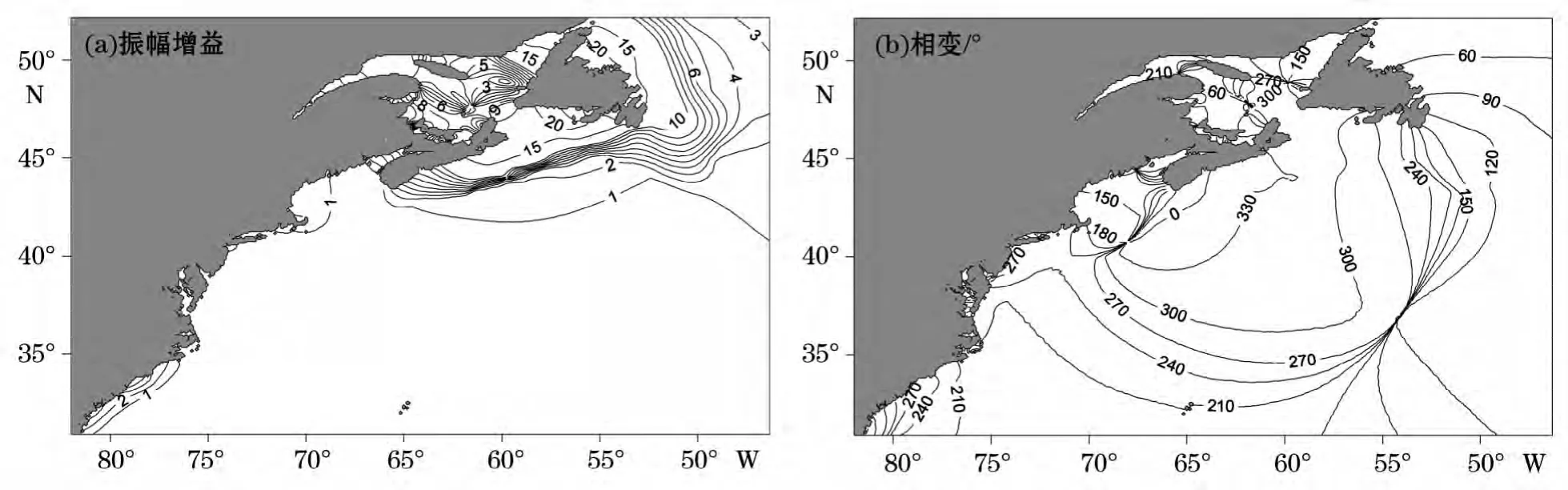
图9 频率（周期）3.16d－1（7.6h）对应的振幅增益和相变空间分布图Fig.9 The spatial distributions of the amplitude gain and phase change for the frequency（period）of 3.16d－1（7.6h）

3 结语

本文采用数值方法研究了芬迪湾、缅因湾和圣劳伦斯湾的潮汐共振情况，并将芬迪湾和缅因湾作为一个系统进行了研究。研究结果发现缅因－芬迪湾系统最强共振的周期约为13.0h，与N2分潮（12.66h）较为接近。其值大约等于Garrett［6］和Godin［10－11］估计值的中数，因而可能更合理。数值与根据陆架共振计算的结果比较一致，因而系由陆架共振所引起。而芬迪湾次强共振的周期约为9.2h，这同芬迪湾四分之一波长共振周期9.3h较为接近。

圣劳伦斯湾的共振现象主要体现在其东北部海区，在这一海区通过海峡与大西洋相连，共振周期约为9.2h，这可能是由半波长共振引起的。由于潮汐不存在这一周期的分潮，故圣劳伦斯湾不存在潮汐共振现象，与 Godin［11］结论一致。

（References）：

［1］LAMB H.Hydrodynamics［M］.Oxford：Cambridge University Press，1993.

［2］PROUDMAN J.Dynamical Oceanography［M］.London：Methuen，1953.

［3］HONDA K，TERADA T，ISITANI D.On the secondary undulations of oceanic tides［J］.The London，Edinburgh，and Dublin Philosophical Magazine and Journal of Science，1908，15（85）：88－126.

［4］RAO D.Natural oscillations of the Bay of Fundy［J］.Journal of the Fisheries Board of Canada，1968，25（6）：1097－1114.

［5］DUFF G.Tidal resonance and tidal barriers in the Bay of Fundy system［J］.Journal of the Fisheries Board of Canada，1970，27（10）：1701－1728.

［6］GARRETT C.Tidal resonance in the Bay of Fundy and Gulf of Maine［J］.Nature，1972，238：441－443.

［7］GARRETT C.Normal modes of the Bay of Fundy and Gulf of Maine［J］.Canadian Journal of Earth Sciences，1974，11（4）：549－556.

［8］PLATZMAN G.Two－dimensional free oscillations in natural basins［J］.Journal of Physical Oceanography，1972，2（2）：117－138.

［9］KU L，GREENBERG D，GARRETT C，et al.Nodal modulation of the lunar semidiurnal tide in the Bay of Fundy and Gulf of Maine［J］.Science，1985，230（4721）：69－71.

［10］GODIN G.The resonant period of the Bay of Fundy［J］.Continental Shelf Research，1988，8（8）：1005－1010.

［11］GODIN G.On tidal resonance［J］.Continental Shelf Research，1993，13（1）：89－107.

［12］DEFANT A.Physical oceanography［M］.Oxford：Pergamon Press，1961.

［13］WEBB D.On the shelf resonances of the Gulf of Carpentaria and the Arafura Sea［J］.OceanScience Discussions，2012，9（2）：443－497.

［14］MUNK W，CARTWRIGHT D.Tidal spectroscopy and predication［J］.Philosophical Transactions for the Royal Society of London.Series A，Mathematical and Physical Sciences，1966，259：533－581.

［15］SUTHERLAND G，GARRETT C，FOREMAN M.Tidal Resonance in Juan de Fuca Strait and the Strait of Georgia［J］.Journal of physical oceanography，2005，35（7）：1279－1286.

［16］ROOS P，VELEMA J，HULSCHER S，et al.An idealized model of tidal dynamics in the North Sea：resonance properties and response to large－scale changes［J］.Ocean dynamics，2011，61（12）：2019－2035.