混合邻域结构的粒子群算法

张泽星

（石家庄经济学院网络信息安全实验室，河北石家庄 050031）

粒 子 群 算 法（particle swarm optimization，PSO）是KENNEDY 和EBERHART 两位博士于1995年提出的新型进化算法［1］，因其具有易于实现、精度高、收敛快等优点，且在解决实际问题中表现优异，自提出以来便受到了学术界的广泛重视［2－3］。然而，标准PSO 算 法 的 缺 点 也 是 明 显 的［4］，首先容易出现陷入局部极值、早熟收敛或停滞现象。其次，PSO 的性能也依赖于算法参数。为此，研究人员分别采用粒子群初始化、邻域拓扑、参数选择和混合策略等改进措施克服上述不足［4］。

为避免由于粒子向自身历史最佳位置和群体历史最佳位置聚集，形成粒子种群的快速趋同效应现象，在分析不同拓扑结构对算法性能影响的基础上，结合全局模型，同时使用无标度网络作为局部邻域拓扑，在标准测试函数上的实验结果表明，该方法可有效平衡算法的开采和挖掘能力，性能良好。

1 全局模型与局部模型

1.1 标准粒子群算法（SPSO）

基本粒子群算法的数学表示如下：设搜索空间为D维，由n个粒子组成种群；用Xti和Vti分别表示第i个粒子在第t步迭代时所处的位置和飞行速度：Xti＝（xti1，xti2，…，xtiD），Vti＝（vti1，vti2，…，vtiD）；记pti和ptg分别为到第t次迭代为止，第i个粒子自身经历的最佳位置和种群经历的最佳位置。

每个粒子的位置按如下公式变化：

式中：w为惯性因子；d＝1，2，…，D；i＝1，2，…，n；t为当前迭代次数；c1，c2为正的常数，称为加速因子；r1和r2为［0，1］区间内的均匀随机数。

式（1）将其他全部粒子视为当前粒子的邻域，pgd是该邻域中粒子的历史最佳位置，该模型被称为全局模型。除了全局模型外，EBERHART［5］等最早提出了局部版的粒子群算法。局部模型将式（1）中的pgd替换为pld，pld代表当前粒子的拓扑邻域中所有粒子的最优位置。目前，已被广泛接受的结论是：邻域结构是决定PSO 算法效果的极重要因素，这是因为邻域结构决定了优秀等位基因的传播和混合，从而影响到搜索性能［6］。前人的研究表明［7］，全局模型收敛速度较快，具有较强的局部搜索能力，但鲁棒性较差；局部模型收敛速度较慢，但具有较强的全局搜索能力，鲁棒性较好。本文将这2种模型结合在一起，设计了一种新的混合模型。

1.2 邻域拓扑分析

式（1）被称为全局模型，该模型中，粒子i的邻域集合为P－｛i｝，其中，P为全体粒子。也就是说，任何2个粒子之间均存在着“联系”，从而，全局模型的邻域拓扑为一个完全图。

局部模型的邻域拓扑主要有［7－8］1）环形拓扑：所有粒子首尾互连构成一个环。2）星形拓扑：以其中一个粒子为中心，该中心与相邻的其他粒子进行信息交换，且其他粒子之间互不联系。3）塔形拓扑：也称K面体结构，粒子分布在K面体的K个顶点上，然后所有K面体再相互连接起来。4）冯·诺依曼拓扑：用三维网格的形式把粒子与它上下左右4个最邻近的粒子相互连接，形成立体网状结构。

上述提到的拓扑结构特点主要有2个：静态性和规则性，即拓扑结构是事先给定的规则图。考虑到个体交互的随机性，研究人员将动态变化或非规则的拓扑结构引入局部模型，做法分为3类：第1类是从空间距离的角度划分邻域。早在1999年，SUGANTHAN［9］引入一个时变的欧氏空间邻域算子：在搜索初始阶段，将邻域定义为每个粒子自身；随着迭代次数的增加，将邻域范围逐渐扩展到整个种群。再如：范成礼［10］等提出了带审敛因子的变邻域粒子群算法，有效避免了常规PSO 算法在复杂多峰函数的求解过程中容易陷入早熟收敛的问题，提高了全局搜索能力。第2类单纯从粒子的社会关系角度进行邻域动态或非规则划分，如：彭虎［11］等将随机拓扑和冯·诺依曼拓扑相结合形成动态社会关系邻域；GONGSUN［12］等将基于小世界网络的邻域结构引入到粒子群优化求解中。还有一类借助子群或簇来建立信息交换的拓扑结构，如：郭文忠［13］等基于“簇”思想，对粒子间距离进行重新定义并给出了相应的动态邻域PSO 算法。再如：倪庆剑［14］等引入了一种粒子群信息共享方式——多簇结构，进而提出了动态可变拓扑策略以协调动态概率粒子群优化算法的勘探和开采能力。针对不同的优化问题，这些拓扑的性能表现各异；但总的来说，随机拓扑往往对大多数问题能表现出较好的性能［4］。

2 混合拓扑模型

2.1 使用混合拓扑的PSO

使用复杂网络作为局部邻域首先要解决的问题是建立复杂网络。建立复杂网络的算法有许多，本文采用无标度网络作为邻域拓扑，建立该类型网络的最知名的算法莫过于BA 网络模型。BA 模型具体描述如下［15］。

假设网络最初有m0个节点。每一次加入一个新节点，每次加入的新节点通过m（m≤m0）条新加入的连接边与网络中已有的m个节点相连。每个新节点与节点i相连的概率∏（ki）依赖于节点i的度ki，且该概率服从如下规则：

重复加入t个节点后，将得到一个有N＝t＋m0个节点和mt条边的网络。

其次，需要建立粒子与网络节点之间的映射，映射的方法有2种：1）当节点数与粒子数相等时，可以采用一对一的映射；2）当节点数大于粒子数时，可以采用多对一的映射，即一个粒子对应网络上多个节点。本文采用的是第2种方式。不妨设映射函数为f：i→N（i），它将粒子i映射到网络节点集N（i）上，N（i）＝｛N1（i），N2（i），…，N｜N（i）｜（i）｝；其中，网络节点Nj（i）（j＝1，2，…，｜N（i）｜）的邻居集合为｛Nj1（i），Nj2（i），…，N｜Nj（i）｜（i）｝。在迭代时，按如下步骤确定粒子i的邻域。

步骤1：借助映射函数，确定i对应的网络节点集合N（i）；

步骤2：随机从N（i）中取一个元素，不妨设为Nj（i）；

步骤3：将Nj（i）的邻居作为i的邻域。

基于无标度网络邻域结构的粒子群算法的主体流程如下。

步骤1：初始化运行参数；

步骤2：初始化速度和位置；

步骤3：计算适应度；

步骤4：创建无标度网络；

步骤5：建立粒子与网络节点的映射关系；

步骤6：WHILE（满足迭代条件）；

6.1 如果最优解没有更新；

6.1.1 为每个粒子产生邻域；

6.2 对每个粒子；

6.2.1 从其邻域中找到最优个体；

6.2.2 更新速度与位置；

6.3 更新个体最优历史；

6.4 更新种群最优历史；

步骤7：返回最优个体。

上述算法中，速度更新公式如下：

式中：Px，Pl，Pg分别代表粒子的历史最优、邻域最优及种群最优；w，c分别为惯性因子和加速因子；r1，r2，r3分别为［0，1］内的3个随机数。

位置更新公式如下：

2.2 算法分析

全局模型的拓扑是一个完全图（规则图）；大量研究结果表明：使用随机拓扑的粒子群算法效果良好。然而，现实中的网络即非规则图也非随机图，大多数现实网络都呈现无标度特性。因此，使用无标度网络作为邻域拓扑使粒子的交互结构更贴近现实。从式（4）来看，速度更新考虑了粒子自身的历史、邻域和种群三方面信息，从另外一个角度来说，本文设计的是介于全局和局部模型之间的混合模型。

从上面的描述来看，粒子的邻域是动态变化的，粒子i映射的网络节点集为N（i）＝｛N1（i），N2（i），…，N｜N（i）｜（i）｝，粒子的邻域取决于：1）从N（i）中随机抽取的是哪个网络节点；2）随机抽取的网络节点（不妨设为Nj（i））的度及其相邻节点。

由于无标度网络符合幂律分布，设在网络中随机抽取到度为k的节点概率为p（k），可以证明［15］：

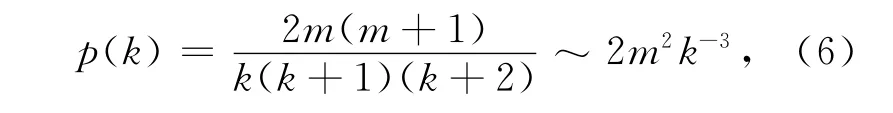
该式说明，度越大的节点出现在网络中的概率越小。也就是说，大多数粒子的邻域规模都比较小。

在空间和时间复杂度方面，与标准粒子群算法相比，本文算法空间上需要额外存储复杂网络；时间上增加了寻找粒子邻域的支出。收敛性方面，由于并未从根本上改变粒子群算法的流程，因此，本文算法的收敛性证明与标准粒子群算法一致。

3 实验结果

借助实验，需要探究的问题包括：1）算法的性能比较；2）算法的收敛情况；3）不同维度与不同运行参数下的算法性能；4）复杂网络节点数与算法性能的关系；5）运行时间的比较分析等等。由于篇幅关系，本文仅针对于问题1）和问题2）进行详细的实验及其结果分析。

3.1 实验设计

实验采用的3个经典测试函数分别描述如下。

这3个函数各有特点，如图1所示，f1有明显的全局最优，梯度变化明显；f2在相对“平坦”的区域有许多局部最优；f3的梯度变化不明显。相比之下，f1的全局最优最容易寻找；f2和f3寻全局最优解则都比较困难，分别要求算法具有较强的逃逸局部最优的能力（也可以说是勘探能力）和持续进化的能力（或说是开采能力）。

比较算法来自于SPSO2011［16］，其源代码从文献［17］获取。每个测试函数上独立运行10次，分别记录：在所有运行中找到最好解（记为HB）、每次独立运行最优解的平均值和方差（分别记为MEAN和STD）。从某种程度上讲，HB越好则算法的开采能力越强。平均数反应的是数据的集中趋势，越集中说明算法性能越稳定；方差反映的是离散程度，从某种意义上讲，越离散说明算法鲁棒性越差。

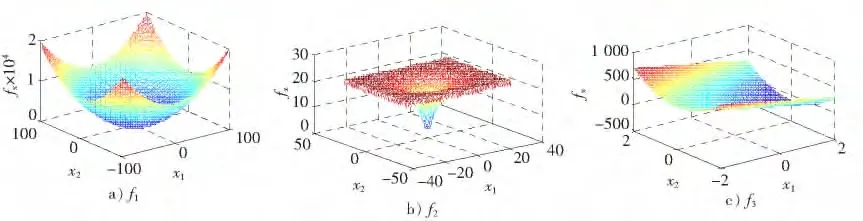
图1 测试函数图形Fig.1 Figure of test functions

3.2 实验结果及分析

实验一：性能比较。函数维度D＝20，网络节点数取为100，粒子个数为30。公平起见，其他参数设置同所比较的SPSO2011 代码［17］。实验结果见表1，方便起见，以下将本文算法简记为NPSO。表1中，指标值更好的结果用黑体表示。不难看出，本文算法全面超过了SPSO。

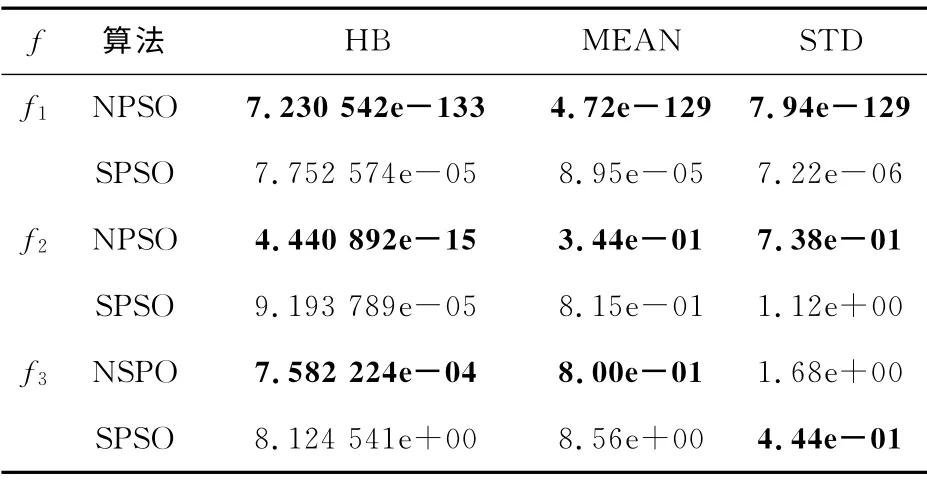
表1 性能比较结果Tab.1 Compared results of performance

从表1来看，在f1上，NSPO 取得的STD 非常小且其MEAN 接近HB，说明NPSO 总能为f1找到非常优异的解。这得益于f1仅有一个全局最优，而且梯度变化明显（见图1）。但尽管如此，SPSO 仅能找到7.752 574e－05这样的解，远次于NPSO 的7.230 542e－133。这可能是因为在f1的“底部”，地势较平坦，尽管全局不存在局部最优，但SPSO 在较平坦的底部地形上，“前进”非常困难，而NPSO针对于这样的地形，寻优能力优越。

在f2上，NSPO 的HB指标值远优于SPSO，但两者均值相差不大。实验中发现，NSPO 在f2上，多数情况下能找到10－15这一数量级的解，偶尔找到100这一数量级的差解。对应的，SPSO 最好解的数量级在10－5，最差解的数量级为100。这反应出NSPO 跳出局部最优解的能力要强于SPSO。但由于f2存在大量的局部最优，尽管NSPO 的勘探能力强于SPSO，但仍有很大提升空间。

在f3上，NSPO 的STD 大于SPSO，但HB 小于SPSO，说明NSPO 具备找到更好解的能力。由于f3的梯度信息不明显甚至存在“误导”的梯度信号，比如：从当前位置向左寻找确实能使得解得以进化，但如果正确的方向应该是向下，则“向左”的梯度可能会误导算法走向错误的方向。如此，则会大大降低算法的搜索效率。正因为此，最好情况下，NSPO只找到了10－4这一数量级的解。

实验二：收敛性实验。收敛性结果可以从某种程度上反应出算法是否早熟；从某种程度上揭示参数对收敛性及性能的影响等。图2给出了NPSO与SPSO 一次独立运行中收敛结果的比较示意图，本实验采用的运行参数完全同于实验一。图2a），c），e）分别是NSPO 在f1，f2，f3上的收敛示意图；图2b），d），f）分别是SPSO 在3个测试函数上的收敛示意图。

图2b）明显反应出SPSO 在f1上存在早熟或停滞现象，最优解仅仅进化了100余次。从图2a）看出，NSPO 在f1上进化了近2 000次。

在f2上，要求算法必须不断地逃逸出局部最优。图2c）和图2d）显示，NSPO 的进化次数是SPSO 的3倍多。这说明NSPO 的逃逸能力要强于SPSO，但终究还是在进化了500余次后陷入了无法逃出的某个局部解。这种情况下，增加迭代次数对提高算法性能显然是无益地。

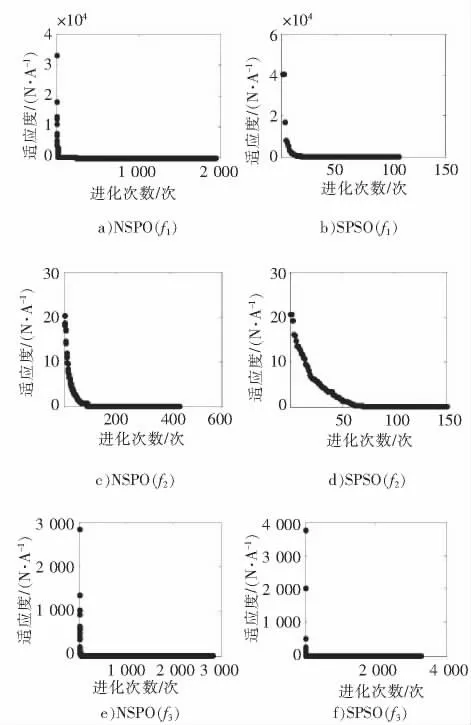
图2 收敛对比结果Fig.2 Compared results of convergence

在f3上，不存在局部最优解，但存在大量的“误导”梯度。从图2d）和图2f）可以看出，2种算法均进化了3 000 余次，在一定的迭代次数内，无论是NSPO 还是SPSO，算法总能进化，但这种持续的进化最终使得2种算法均出现“南辕北辙”的现象。但总体上，NSPO 克服“误导”梯度的能力要更强一些。

4 结 语

本文提出的算法综合了全局和局部模型，粒子的局部邻域拓扑根据无标度网络的结构确定。实验结果表明，借助无标度网络作为邻域拓扑是可行的。与标准PSO 的全局模型相比，本文算法在避免早熟、陷入局部最优、停滞这些缺点上，有较好的改善。新算法的适应性、鲁棒性更强，具有较强的可应用性和拓展性。

／References：

［1］ KENNEDY J，EBERHART R C.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks［C］.Piscataway：IEEE Press，1995：1942－1948.

［2］ RADA－VILELA J，JOHNSTON M，ZHANG M J.Deception，blindness and disorientation in particle swarm optimization applied to noisy problems［J］.Swarm Intelligence，2014，8（4）：247－273.

［3］ SHEN M，ZHAN Z H，CHEN W N，et al.Bi－velocity discrete particle swarm optimization and its application to multicast routing problem in communication networks［J］.IEEE Transactions on Industrial Electronics，2014，61（12）：7141－7151.

［4］ 戴 朝 华.粒 子 群 优 化 算 法 综 述［EB／OL］.http：／／www.doc88.com／p－30490875816.html，2010－05－24.DAI Zhaohua.A Suvery of Particle Wwarm Optimization［EB／OL］.http：／／www.doc88.com／p－30490875816.html，2010－05－24.

［5］ EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory［A］.Proceedings of the 6th International Symposium on Micro Machine and Human Science［C］.［S.l.］：IEEE Xplore，1995：39－43.

［6］ PAYNE J L，GIACOBINI M，MOORE J H.Complex and dynamic population structures：Synthesis，open questions，and future directions［J］.Soft Computing，2013，17（7）：1109－1120.

［7］ KENNEDY J.Small worlds and mega－minds：Effects of neighborhood topology on particle swarm performance［A］.Proceedings of the IEEE Congress on Evolutionary Computation［C］.Washington：IEEE，1999：1931－1938.

［8］ KENNEDY J，MENDES R.Population structure and particle swarm performance［A］.Proceedings of IEEE Congress on Evolutionary Computation［C］.Honolulu：［s.n.］，2002：1671－1676.

［9］ SUGANTHAN P N.Particle swarm optimiser with neighbourhood operator［A］.Proceedings of the IEEE Congress on Evolutionary Computation［C］.Piscataway： NJ，1999：1958－1962.

［10］ 范成礼，邢清华，范海雄，等.带审敛因子的变邻域粒子群算法［J］.控制与决策，2014，29（4）：696－700.FAN Chengli，XING Qinghua，FAN Haixiong，et al.Particle swarm optimization and variable neighborhood search algorithm ith convergence criterions［J］.Control and Decision，2014，29（4）：696－700.

［11］ 彭虎，张海，邓长寿.动态邻域混合粒子群优化算法［J］.计算机工程，2011，37（14）：211－213.PENG Hu，ZHANG Hai，DENG Changshou.Dynamic neighborhood hybrid particle swarm optimization algorithm［J］.Computer Engineering，2011，37（14）：211－213.

［12］ GONGSUN Y J，ZHANG J.Small－world particle swarm optimization with topology adaptation［A］.Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation［C］.［S.l.］：［s.n.］，2013：25－32.

［13］ 郭文忠，陈国龙，洪玉玲.求解TSP问题的动态邻域粒子群优化算法［J］.漳州师范学院学报，2007，20（2）：37－41.GUO Wenzhong，CHEN Guolong，HONG Yuling.Dynamic neighborhoodd particle swarm optimization for TSP［J］.Journal of Zhangzhou Normal University，2007，20（2）：37－41.

［14］ 倪庆剑，张志政，王蓁蓁，等.一种基于可变多簇结构的动态概率粒子群优化算法［J］.软件学报，2009，20（2）：339－349.NI Qingjian，ZHANG Zhizheng，WANG Zhenzhen，et al.Dynamic probabilistic particle swarm optimization based on varying multi－cluster structure［J］.Journal of Software，2009，20（2）：339－349.

［15］ BARABASI A L，ALBERT R.Emergence of scaling in random networks［J］.Science，1999，286：509－512.

［16］ CLERC M.Standard Particle Swarm Optimisation：From 2006 to 2011［EB／OL］.https：／／hal.archives－ouvertes.fr／hal－00764996，2012－09－23.

［17］ OMRAN M G H.Standard PSO Source Code Version 2011［EB／OL］.http：／／www.particleswarm.info／standard＿pso＿2011＿c.zip，2011－11－04.