基于黏性材料的直根抗拔强度研究

申 辉，郭晓晓

（河北省电力勘测设计研究院，河北石家庄 050031）

21世纪初，有关绿色植被和边坡稳定性关系的研究便开始在欧美展开。传统上，一般采取水泥护坡或者土钉墙等手段来对土质边坡进行加固。然而在一些居住环境狭窄的地区，比如中国香港，居民对于窗外随处可见冷色调的土钉墙支护提出了不满［1］。于是，如何通过植被覆盖来提高边坡的稳定性，满足工程需求与居民需求，已成为一个重要的研究方向。

根据TIEN［2］等的研究，树根与土体的接触在树根的生物特性作用下，实际上是与树根接触的那部分土体的属性改变了，使其变成了一种类似胶状的物体。这使得土壤－树根（以下简称为根－土）关系不单单是摩擦模型这么简单。因此，本文通过在已有根－土摩擦模型上添加黏性材料，变相的让直根在拔出过程中承担一部分土体的质量，来对根－土关系和抗拔强度进行模拟，并得出了一些有意义的结果。

1 基本理论

树根的拔出实际上是一种对稳定局面的破坏行为。而定义一个破坏行为需要2个关键标准：破坏在什么标准下启动和破坏启动之后在什么标准下发展，后文简称“两个标准”。图1展示的就是一个典型的基于原位试验的直根拔出力同直根位移的关系曲线［3］。从图1可知，树根的拔出分成3个阶段：峰前阶段、峰值点和峰后阶段。随着拔出力的加大，树根开始逐步被拔出。在到达抗拔力峰值的瞬间，破坏行为开始。之后拔出力沿着破坏发展曲线逐步下降直至降为零，也就是树根被完全拔出。而数值模拟的目标就是对这个曲线进行定性和定量的复盘。

图1 直根拔出力－拔出位移曲线Fig.1 Pull－out strength of tap－root versus displacement

1.1 摩擦模型

Abaqus中的库仑摩擦模型通过下述的2个对应关系来对“两个标准”进行模拟［4］。关系A 定义（第1条标准，也就是广为人知的库仑摩擦定律）：摩擦力跟作用在摩擦面上的正压力成正比。进而可以通过定义摩擦系数或者极限静摩擦力来定义这一标准。关系B 所定义的就是第2 条标准。可以赋予摩擦系数一个衰减值，使得摩擦系数在破坏发生之后逐步下降。然而在之前进行的模拟结果中可以发现［5］：影响峰后阶段的关键因素不仅仅是衰减值，还有滑动速率，如式（1）所示。

式中：μ是摩擦系数衰减曲线；μk是静摩擦系数；μs是动摩擦系数；dc是摩擦系数衰减值；γcq是滑动速率。

当直根的拔出被模拟为通过将总位移分成多个小位移，在多个相同的小时间增量下来施加的时候，滑动速率实际上是不变的。由于本文主要研究根－土关系模拟，不涉及滑动速率的改变，这就直接导致了Abaqus库仑摩擦模型很难对峰后阶段进行修正。同时，因为树根的杨氏模量一般都不大，在拔出力越来越大的影响下，树根直径会发生减小的现象。一旦直径减小到使得根－土之间在某一个点出现空隙，这个点的摩擦力也会瞬间降至为零。上述2个原因就是导致摩擦模型得出的抗拔强度小于理论值的原因。

1.2 黏性材料

Abaqus中的黏性材料是建立在线弹性的牵引分离行为之上。线弹性的牵引分离行为假设一切破坏都是以线弹性作为起始属性。线弹性是通过将接触面的名义应力同名义应变联系起来，组成弹性矩阵来表达的。其中，名义应力是在每一个积分点的应力分量，是一种整体的等效应力，并不是实际作用于结构局部的应力。相同的，名义应变是每一个积分点的各方向的分离值除以原始厚度所得到的。

Abaqus提供了多种标准来定义破坏的启动点，比如通过定义积分点的三向应力、三向应变或者应力应变的平方值。在之后的模型中采取的是最大名义应变标准（maximum nominal strain criterion），破坏将在任意一个最大名义应变比达到1 的时候启动，即

式中：ε代表即时的应变值；ε0代表设定的最大应变值；角标n，s，t分别代表接触面法向方向和接触面的2个切向方向。

在破坏启动之后，就需要定义破坏的发展。Abaqus中的黏性材料是通过弱化材料刚性来达到对破坏发展的定义。具体来说，可以假定一个破坏标量值D，这个值描述了材料整体的破坏程度，并且可以捕捉其他与破坏有关的动态的力学影响。随着破坏的发展，D将会随着接触力的变化逐步从0增长到1。在牵引分离行为中，破坏启动后的法向应力可以定义如下：

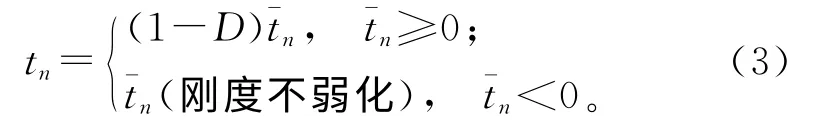
式中是未破坏时的即时应变推算出的法向应力分量，另外2个切向的应力分项与本公式相似。

通过上述表达，本文考虑将摩擦模型同黏性材料有机地结合在一起，以得到更精准的结果。具体来说，因为摩擦模型在峰前阶段，或者树根在滑动开始之前，仍然是基于静摩擦力的接触关系，所以摩擦模型仍然在这一阶段发挥作用。但是正如前文所述，随着拔出力的变大，摩擦模型在一些点也会逐渐失效，所以，在根－土之间加入1层黏性材料，用以模拟被生物特性改变的土体。黏性材料的特性使得当树根的某一点的直径逐步减小时，根－土之间的力学交互关系也不会解除。

2 直根－土体模拟

2.1 概述

本文采用黏性材料对根－土交互关系进行模拟，来弥补库仑摩擦模型的结果偏小的缺陷，并且计算不同几何模型的直根的抗拔强度。根据TIEN 的研究，被树根植物特性改变的那层胶状土非常薄，一般不会超过树根直径的1／10，并且强度也远小于离直根较远的土体的强度。然而，就是这一层胶状土体使得根－土关系不单单是摩擦关系，而变成了树根在克服摩擦力的同时，也要变相承担一部分土体的质量，这也是选择黏性材料进行根－土分析的根本原因。这层黏性材料就如同一组平行排列的没有重力的弹簧，只不过这组弹簧在树根拔出方向的抗拔强度非常低。弹簧开始时全部与直根垂直，并且因为土体侧压力的原因，弹簧全部处于临界压缩状态。弹簧被固定在土体上，但是弹簧与直根的接触关系为摩擦模型。随着直根的拔出，这层弹簧会被向上拉伸，当拔出方向的应变达到了弹簧的抗拔强度，弹簧即刻失效。本文这种设计，使得黏性材料随时都与树根接触，使得摩擦模型不会失效；黏性材料随时根据竖向应变定义的标准，对直根有一个向下的拉力。

2.2 模拟方法

整个数值模拟过程是基于有限元原理构建的Abaqus 6.10 版本。为了方便对黏性材料进行测试，只有直根参与模拟，并且被假定为圆柱体。所以直根和土体都被设定为轴对称、可变形的壳分析构件。考虑到树根可影响的土体范围有限，所有模型的土体亦是圆柱体，半径是土体圆柱体半径的4倍，长度是1.5 倍。并且在直根和土体之间加入了1层黏性材料参与根－土关系模拟，这层黏性材料厚度不超过土体圆柱体半径的1／5，如图2所示。需要说明的是，这层黏性材料并没有作为独立的构件出现，而是将土体的一部分划分出去，并且独立赋值，这样既符合根－土关系的实际情况，亦简化模型复杂度［6］。

图2 根－土模型展示Fig.2 Root－soil model

直根、黏性材料和土体都被假定为弹性材料。根据之前的研究成果，库仑摩擦模型可以很好地模拟树根峰前阶段和峰值，所以树根与黏性材料的交互关系被设定为库仑摩擦模型，摩擦系数为0.5。黏性材料采取最大名义应变标准来定义，因为是单纯的拔出，所以ε0s和ε0n都被赋予了一个较大的值。而ε0t被设定为0.01。具体的输入参数见表1。

表1 物理参数输入表Tab.1 Inputed physical parameters

其中，重力加速度为10 m／s2，侧压力系数为0.43，ε0t＝0.01，摩擦系数为0.5。

有限元分析包括2步：第1步，施加重力，并通过修改inp文件添加初始地应力；第2步，在直根顶部施加一个向上的位移，模拟树根的拔出。整个模型底部被三轴固定，禁止出现三轴方向的位移和转动；模型两侧被X轴固定，禁止出现X轴方向的位移和Y，Z轴的转动。模型整体被划分成四节点双线性轴对称四边形（CAX4）。

2.3 结果输出

为了得到拔出力同拔出长度的曲线，本文提取树根顶部竖向的应力值S22，将其在顶部平面上积分便得到了树根顶部的荷载。因为树根顶部的荷载同拔出力是一对相互作用力，便得到了拔出力。具体计算见式（4）。

式中：S22为竖向应力；r为树根半径。

2.4 模拟结果

首先，在一个直根半径为5 mm、长度为100 mm 的样本上进行了一组可行性极限实验。实验分2次进行：第1次为库仑摩擦模型，土体不添加黏性材料；第2次为添加了黏性材料的库仑摩擦模型。2次实验都将直根全部拔出，并按照前文所述计算了拔出力，见图3。

图3 两种模型拔出力的比较Fig.3 Force－displacement curves for the two models

从图3中不难看出，加入了黏性材料的模型的极限拔出力明显高于未加入黏性模型的拔出力。

研究直根上不同位置节点的竖直力随时间变化曲线，发现库仑摩擦模型的拔出力在抵达峰值后，在某些节点会突变至零，说明根－土之间出现了空隙；然而，加入了黏性材料的模型，这些节点在抵达峰值之后，会逐渐降低。这证实了黏性材料对摩擦模型有积极的修正作用，也说明了在对直根－土体接触面添加1层薄的黏性材料后可以提高模拟的准确度，并且图3也同图1所示的原位试验曲线大致相近。拔出力都是在抵达极限之后，出现了快速式的下降［7］。

本文进行了多次针对几何变化的实验，采用了直径－长度矩阵来对直根与土体做出几何安排，所有模型的黏性材料宽度不超过直根直径的1／5，并且直根皆为圆柱体，详见表2。

表2 直径－长度组几何安排表Tab.2 Diameter－length matrix

本文对表2所示的所有模型都进行了模拟，但限于篇幅，只选取了一些具有代表性的结果展示如下。需要说明的是，因本文关心的是抗拔强度，所以所有实验结果都以是否达到极限抗拔强度为实验终止标准，不再进行将直根全部拔出的实验。

如图4所示，如果直径固定，只改变直根长度，极限拔出力基本成线性增长，这同之前的实验结果是相符合的：拔出力是和直根同土体的接触面积有关。相似的，如果将长度固定，改变直径，也可以得到如图4所示的类似结果。说明在加入黏性材料之后，仅对拔出曲线做出了定量的修改，没有造成不利的影响。

将直根的体积固定为2 500cm3，模型仍然保持为圆柱体，进而改变直根的长度与直径［8－11］。具体模型的几何安排见表3，结果见图5。最大拔出力并未出现在最大长度或者最大直径的样本上，反而是出现在了直径3mm，长度350mm 的样本上，进一步证明了拔出力是由接触面积决定的这一结论。

图4 直径固定组的拔出试验Fig.4 Pull－out test results for diameter－fixed group

表3 体积固定组几何安排表Tab.3 Geometry arrangement table of volume－fixed group

图5 体积固定组的拔出实验Fig.5 Pull－out test results for volume－fixed group

3 结 语

Abaqus中自带的黏性材料可以达到消除根－土之间空隙的效果［12－15］，通过设置一个较低的破坏标准，使得这层黏性材料对结果未有不利影响，反而模拟出较好的结果，进一步修正了之前的摩擦模型。

／References：

［1］ CAMPBELL S D，DIAS A.The Use of Soil Bioengineering Measures to Repair Selected Natural Terrain Landslides in Hong Kong（25th Annual Seminar）［M］.Hong Kong：The HKIE Geotechnical Division，2005.

［2］ TIEN H W，MCOMBER R M，RONALD T E，et al.Study of soil－root interaction［J］.Geotech Eng，1988，114（12）：1351－1375.

［3］ SCHWARZ M，COHEN D，OR D.Root－soil mechanical interactions during pull out and failure of root bundles［J］.Journal of Geophysical Research：Earth Surface，2010，115：403－407.

［4］ The 3DExperience Company.ABAQUS Analysis User’s Manual［M］.［S.l.］：［s.n.］，2011.

［5］ GUO Xiaoxiao.Pull－out strength of root－geological engineering and mining exploration in central Asia［A］.The XVⅢKerulien International Conference on Geology［C］.Aussino：Academic Publishing House，2013：152－170.

［6］ DUPUY L，FOURCAUD T，STOKES A.A numerical investigation into factors affecting the anchorage of roots in tension［J］.European Journal of Soil Science，2005，56（3）：319－327.

［7］ DUPUY L，FOURCAUD T，STOKES A.A numerical investigation into the influence of soil type and root architecture on tree anchorage［J］.Plant and Soil，2005，278（1／2）：119－134.

［8］ SCHWARZ M，COHEN D，OR D.Pullout tests of root analogs and natural root bundles in soil：Experiments and modeling［J］.Journal of Geophysical Research：Earth Surface，2011，116：175－177.

［9］ 孔令伟，陈正汉.特殊土与边坡技术发展综述［J］.土木工程学报，2012，45（5）：141－161.KONG Lingwei，CHEN Zhenghan.Advancement in the techniques for special soils and slopes［J］.China Civil Engineering Journal，2012，45（5）：141－161.

［10］ 王兰民.黄土动力学［M］.北京：地震出版社，2003.WANG Lanmin.Loess Dynamics［M］.Beijing：Earthquake Press，2003.

［11］ 郑宏.严格三维极限平衡法［J］.岩石力学与工程学报，2007，26（8）：1529－1537.ZHENG Hong.A rigorous three－dimensional limit equilibrium method［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（8）：1529－1537.

［12］ ZHENG Yingren，TANG Xiaosong，ZHAO Shangyi，et al.Strength reduction and step－loading finite element approaches in geotechnical engineering［J］.Journal of Rock Mechanics and Geotechnical Engineering，2009，1（1）：21－30.

［13］ 彭玉青，张红梅，何华，等.数据挖掘技术及其在教学中的应用［J］.河北科技大学学报，2001，22（4）：21－24.PENG Yuqing，ZHANG Hongmei，HE Hua，et al.Data mining technology and its application in teaching［J］.Journal of Hebei University of Science and Technology，2001，22（4）：21－24.

［14］ 言志信，宋杰，蔡汉成，等.草本植物加固边坡的力学原理［J］.土木建筑与环境工程，2010，32（2）：30－34.YAN Zhixin，SONG Jie，CAI Hancheng，et al.Mechanical analysis of herbaceous plant strengthening slope［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2010，32（2）：30－34.

［15］ 侍倩.植被对斜坡土体土力学参数影响的试验研究［J］.岩土力学，2005，26（12）：2027－2030.SHI Qian.Test research on influence of vegetation on mechanical parameters of soils［J］.Rock and Soil Mechanics，2005，26（12）：2027－2030.