一种引入参数无需确定聚类数的聚类算法

周其林，雷菊阳，王昱栋，张兰兰

（上海工程技术大学机械工程学院，上海 201620）

聚类分析是一种将没有类别标记的对象集按照某种规则分为若干个类，同一类中各对象的属性尽可能相似，不同类中各对象的属性会有较大差异。聚类分析是一种无监督学习方法，能够通过特征数据挖掘出对象的相似性，它在模式识别、特征提取、数据挖掘等领域都有广泛应用［1－3］。

k－均值聚类算法是聚类分析中的经典算法，具有算法简单、收敛速度快等特点［4］。但也有2个缺点：第一是需要事先知道聚类数；第二是初始种群的选取是随机的。近年来，为了解决这两大缺陷，对k－均值聚类算法进行了很多改进，如结合智能优化算法对k－均值聚类算法进行改进，但改进后的算法通常比较复杂，这就使传统k－均值聚类算法简单高效的特点不复存在，算法的收敛性方面也存在不足［5－7］。

1 传统k－均值聚类算法及其缺陷

1.1 k－均值聚类算法

k－均值聚类算法简单，且聚类速度快，这是其最大的优点。k－均值聚类算法包括2个独立的步骤：第1步就是随机地选择k个数据作为聚类中心，其中k值是已知的；第2步就是计算每个点到这k个中心的距离，距离的计算通常采用欧氏距离，如果第i个点到第j个中心的距离最短，则这第i个点就被划分到第j个类中，当所有点都被划分好后，修改中心点的值为该类所有样本的均值，然后再重新计算距离，重新划分，重新计算中心，直到这k个聚类中心不再变化，算法结束［8－10］。

对于向量x＝（x1，x2，…，xn）和向量y＝（y1，y2，…，yn）的欧氏距离定义为

k－ 均值聚类算法的实现：

输入 聚类数k以及样品x＝｛x1，x2，…，xn｝；

输出k个类中每个类所含的样品λ1，λ2，…，λk。

步骤：

Step1 从样品x中随机选取k个数据作为初始聚类中心μ1，μ2，…，μk。

Step2 对于每个点xi，计算其到各中心的距离。

dic＝‖xi－μc‖2，其中c＝1，2，…，k。将它们归于距离最近的类，直到所有的样品都归类完毕。

Step3 计算各类中所有样品特征值的平均值作为新的聚类中心，对于每个簇

Step4 重复Step2和Step3直到聚类中心不再发生改变，算法结束。

1.2 k－ 均值聚类算法的缺陷

k－均值聚类算法最大的缺陷就是要知道确定的聚类数k，但在实际中聚类数k往往是不易得到的，这就使得算法在解决很多聚类问题上有很大的局限性［11－12］。此外，这种算法的初始种群是随机选取的，而初始种群的选取对聚类结果又会产生很大的影响，使得聚类结果不稳定，甚至导致聚类结果失真。这种算法还有一个缺陷，就是易陷入局部最优，使得聚类结果偏离全局最优。

2 新聚类算法

2.1 算法综述

算法中引入惩罚参数λ，这种算法是基于递增思想的聚类算法。首先让聚类数k为1，则所有的样品都属于这一个类，该类的中心为所有样品特征值的平均值，对于每个点，计算其到该中心的距离。当检测到存在点到该中心的距离大于λ时，聚类数k加1，然后重新计算每个点到这k个中心的距离，将每个点划分到距其距离最短的中心的类中，然后根据每类中的样品修改聚类中心，然后再计算每个点到这k个中心的距离；当检测到存在点到这k个中心的最短距离大于λ时，聚类数k再加1，以此迭代下去，直到k收敛，即k的值不再发生变化，此时所有的样品点到这k个中心的最短距离都小于λ，算法结束。

这种算法最大的特色是事先不需要知道聚类数k，而只需确定惩罚参数λ的值即可（λ值的确定方法将会在后文中介绍），这就解决了传统k－ 均值聚类算法的最大缺陷，拓展了其应用范围。其次，这种算法的初始聚类中心为所有样品特征值的平均值，而且对于新增的类，其聚类中心的选取也是根据一定的算法得到确定的点，使聚类结果具有很大的稳定性，这就避免了传统k－均值聚类算法初始中心随机选择而导致聚类结果不稳定，甚至会出现失真的情形。此外，这种算法具有全局性，可以很好地避免聚类陷入局部最优。

对于向量x＝（x1，x2，…，xn）和向量y＝（y1，y2，…，yn）的欧氏距离定义为

算法的实现：

输入 样品x＝｛x1，x2，…，xn｝，惩罚参数λ；

输出 每个类中所含样品λ1，λ2，…，λn，以及簇的个数k。

步骤：

Step1 初始化k＝1，λ1＝｛x1，x2，…，xn｝，初始聚类中心为全局均值μ1。

Step2 计算每个样品点到各中心的距离dic＝‖xi－μc‖，μc为第c个聚类中心，其中c＝1，2，…，k。

Step3 如果mincdic＞λ，令k＝k＋1，且μk＝xi，重复Step2，然后将各点划分到距其最近的簇，属于第j类的样品放在ℓi中，并根据来修改聚类中心，其中｜ℓj｜表示ℓi中样品的个数。本次计算结束条件是聚类中心不再发生变化或者是达到设定的最大迭代次数，否则进入下一步。

Step4 重复Step2和Step3，直到收敛。

2.2 惩罚参数λ 的确定

惩罚参数λ的确定是这种算法的难点，本文给出了确定λ的一种方法。算法中每给定一个λ就可以得到一个k，这样就能得到随λ变化k也变化的趋势，进而通过观察k的变化特征来确定λ的值。不难理解，当λ很小时，聚类数k就会很大，特别地，对于n个样品，当λ为0时，k等于n，而随着λ的增大k会越来越小，而且k变小的趋势会越来越平缓，其中会有很长一段k的值是不变化的，这一段对应的k值就是合理的聚类数，然后在这一段中选取一个合适的λ值。

新的算法和传统的k－均值聚类算法一样，都对球形簇有较好的聚类效果，所以下面就以2个球形簇的聚类问题来进一步说明这样选取λ的合理性。假设这2个球形簇中较大的一个球形簇的半径为r，当λ小于r时，随着λ的增大k的变化是明显的，而当λ大于r时，此时k等于2，而且在很大范围内，k的值是不变化的，直到λ足够大时，k变为1，在这个很大范围内即可选取对应的一个λ值作为合适的惩罚参数。

本文采用的方法是作出聚类数k随参数λ变化的趋势图，从而确定参数λ的值。为了提高计算的速度，可适当限定λ的范围。当λ很小，甚至为0时，聚类数k就等于样本的个数，这样计算量就很大，很耗时，对计算时间影响最大的就是λ的下限，因此有必要对λ的最小值进行限制。首先计算出所有样本点到初始聚类中心的欧氏距离，记最小距离为dmin，最大距离为dmax。λ的下限取为dmin，这样对判断λ的值没有影响，而且大大缩短了计算时间。为了进一步缩短计算时间，对λ的上限也进行限制，根据实际情况，λ的取值一定不会超过dmax，因此可取λ的上限为dmax。

3 实验一：茶叶分类实验与分析

3.1 实验数据

实验针对不同地区的红茶和绿茶，包含6个分类特征，分别是：纤维素、半纤维素、木质素、多酸、咖啡因、氨基酸，对23个样品进行聚类。数据如表1所示。

表1 两种茶叶的化学分析数据Tab.1 Data of the two kinds of tea’s chemical analysis

3.2 数据预处理

一个样品中不同的特征值往往采用不同的度量单位，其值可能相差较大，因此有必要对数据进行预处理以提高数据质量［13］，首先对这23 个样品的各特征的化学分析数据进行预处理，对数据进行最小－最大规范化：

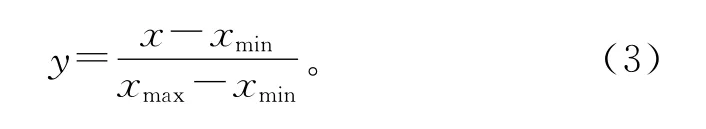
3.3 参数的确定

实验采用Matlab R2008A 开发环境编程实现，如图1所示，以λ为横轴，聚类数k为纵轴建立坐标系，从图1中可以看出，随着λ的增大，聚类数k的值总体上在逐渐减小，当λ的值大于0.14之后，聚类数k的值就稳定在2类，即实验中茶叶的分类数为2类，这与实际情况也是符合的，此时就可以在横轴（0.14，0.22）上选取一个值作为λ的值，不妨取λ等于0.18。

图1 聚类数k随λ 变化的趋势图Fig.1 Trend of k with the increase ofλ

3.4 实验结果

将3.3中得到的λ值0.18输入到Matlab程序中，得到的聚类结果如表2和表3所示。类1代表红茶，类2代表绿茶。

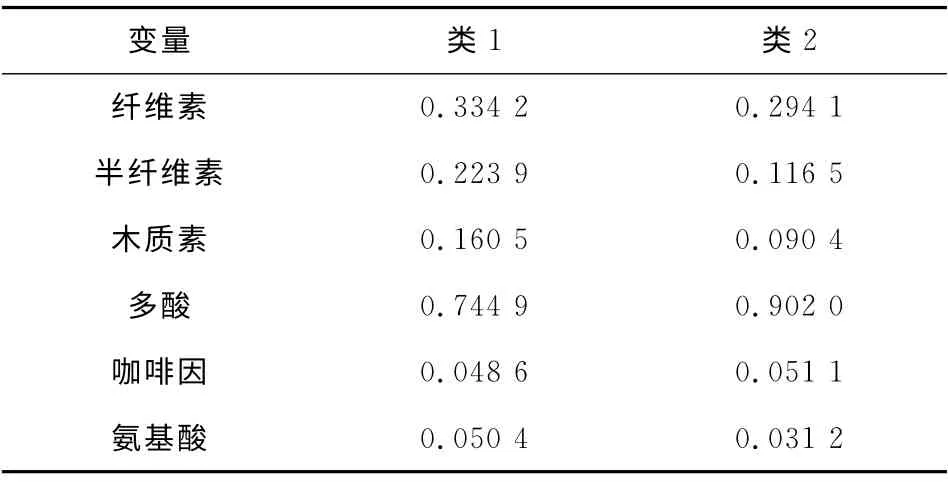
表2 最终聚类中心Tab.2 Final cluster center

3.5 聚类结果分析

由表3的聚类分析最终结果可以看出，这种聚类算法的正确率为91.3%，表现出很好的聚类效果。从表2的最终聚类中心可以看出，红茶（类1）的半纤维素、木质素、氨基酸含量较高，而绿茶（类2）的多酸含量较高，而两种茶的咖啡因和纤维素的含量相差不大。

表3 聚类分析最终结果Tab.3 Final result of cluster analysis

4 实验二：各地区各行业工资水平分析

实验对中国31个不同省、市（不含港、澳、台）的平均工资水平进行了分析，包括15个主要行业的平均工资水平，这15个行业分别是企业、非农企业、事业、农林牧渔业、采矿业、制造业、电力燃气和水的供应业、建筑业、交通运输业、信息传输业、批发和零售业、住宿和餐饮业、金融业、房地产业以及租赁和商务服务业。数据来源于《中国劳动统计年鉴—2010》，具体数据略。

4.1 参数λ 的确定

从图2中可以看出，λ可取0.347 5，此时对应的聚类数k为3。

4.2 实验结果

将λ＝0.347 5输入到Matlab程序中，可得到聚类结果，如表4和表5所示。结果分成3类，由表4可以看出，第1类的平均工资水平很高，第2类居中，第3类较低。

图2 聚类数k随λ 变化的趋势图Fig.2 Trend of k with the increase ofλ

表4 最终聚类中心Tab.4 Final cluster center

表5 聚类结果Tab.5 Final result of clustering

4.3 聚类结果分析

实验的正确率达到100%，实验结果与事实相符，从表5的聚类结果中可知，上海、北京属于第1类，各行业的平均工资水平都高。而天津、浙江、江苏、广东、西藏各行业的平均水平居中，属于第2类。其他的属于第3类，各行业平均工资水平较低。至于为何西藏和另外4个经济较好的省份归为一类，这是因为西藏的物价和人工成本较高，导致平均工资水平较高，符合事实。

5 结 论

传统的k－均值聚类算法是划分聚类算法中最基本的算法，其最大的优点就是简单和高效，因此被广泛应用于各个领域［14］，但这种算法有其固有的致命缺陷，因此其使用受到一定的限制，本文也是针对其最大的2个缺陷对其进行了改进，同时也最大限度地降低改进对其本身优点的影响［15］。改进后算法的特点如下。

1）算法在聚类时不需要知道聚类数k的值，而是引进了参数λ，同时也给出了选择参数λ的具体方法，本文的2个实验也验证了这种方法的可行性。参数λ确定后，将该值输入到Matlab程序中，即可得到聚类数k和聚类结果。

2）算法初始种群的选取不是随机的，而是以全局均值作为初始聚类中心，新增加类的初始中心也是确定的，得到的聚类结果是稳定的。

将这种算法应用到茶叶分类以及各地区各行业平均工资水平分析实验中，也表现出了很好的聚类效果，同时也很好地验证了该算法中惩罚参数选取方法的可行性。

然而，不得不提出的是这种算法和传统的k－均值聚类算法一样，都比较适宜于球形簇的聚类。

／References：

［1］ 李晶皎，赵丽红，王爱侠.模式识别［M］.北京：电子工业出版社，2010.LI Jingjiao，ZHAO Lihong，WANG Aixia.Pattern Recognition［M］.Beijing：Electronic Industry Press，2010.

［2］ 谢娟英，蒋帅，王春霞，等.一种改进的全局k－均值聚类算法［J］.陕西师范大学学报（自然科学版），2010，38（2）：18－22.XIE Juanying，JIANG Shuai，WANG Chunxia，et al.An improved globalk－means clustering algorithm ［J］.Journal of Shaanxi Normal University（Natural Science Edition），2010，38（2）：18－22.

［3］ LIKAS A，VLASSIS M，VERBEEK J.The globalK－means clustering algorithm［J］.Pattern Recognition，2003，36（2）：451－461.

［4］ CHAKRABORTY S J，NAGWANI N K.Analysis and study of incrementalK－means clustering algorithm ［A］.2011 International Conference on communications and Information Science［C］.Chandigarh：Springer－Verlag，2011：338－341.

［5］ ZHONG Wei，ALTUN G，HARRISON R，et al.ImprovedK－means clustering algorithm for exploring local protein sequence motifs representing common structural property［J］.IEEE Transactions on NanoBio Science，2005，4（3）：255－265.

［6］ WANG J T，SU X L.An improvedK－means clustering algorithm［A］.2011IEEE 3rd International Conference on Communication Software and Networks［C］.Xi’an：［s.n.］，2011：44－46.

［7］ 胡伟.改进的层次K均值聚类算法［J］.计算机工程与应用，2013，49（2）：157－159.HU Wei.Improved hierarchicalK－means clustering algorithm［J］.Computer Engineer and Applications，2013，49（2）：157－159.

［8］ 张晓翊，孟德欣，余翠兰.基于K－means算法的学生试卷成绩分析［J］.宁波大学学报（理工版），2010，23（4）：67－70.ZHANG Xiaoyu，MENG Dexin，YU Cuilan.Examination grade analysis based onK－means methods［J］.Journal of Ningbo University（Natural Science and Engineering Edition），2010，23（4）：67－70.

［9］ TIAN Jinlan，ZHU Lin，ZHANG Suqin，et al.Improvement and parallelism ofk－means clustering algorithm［J］.Tsinghua Science and Technology，2005，10（3）：277－281.

［10］ 龙钧宇.基于均值聚类和决策树算法的学生成绩分析［J］.计算机与现代化，2014（6）：79－83.LONG Junyu.Analysis of student’s achievement based on mean cluster and decision tree algorithm［J］.Computer and Modernization，2014（6）：79－83.

［11］ ZHANG Chunfei，FANG Zhiyi.An improvedK－means clustering algorithm［J］.Journal of Information and Computational Science，2013，10（1）：193－199.

［12］ HUANG Xiuchang，SU Wei.An improvedK－means clustering algorithm［J］.Journal of Networks，2014，9（1）：161－167.

［13］ ZHANG Yuhua，WANG Kun，LU Heng，et al.An improvedk－means clustering algorithm over data accumulation in delay tolerant mobile sensor network［A］.2013 8th International Conference on Communications and Networking in China（CHINACOM）［C］.Guilin：［s.n.］，2013：34－39.

［14］ ALIAS M F，ISA N A M，SULAIMAN S A，et al.Modified movingk－means clustering algorithm ［J］.International Journal of Knowledge－based and Intelligent Engineering Systems.2012，16（2）：79－86.

［15］ 王莉，周献中，沈捷.一种改进的粗k均值聚类算法［J］.控制与决策，2012，27（11）：1711－1714.WANG Li，ZHOU Xianzhong，SHEN Jie.An improved roughk－means clustering algorithm［J］.Control and Decision，2012，27（11）：1711－1714.