“RPR教学模式”的实践与探索

金丽萍

摘 要：数学教育历史悠久，教学模式推陈出新，在新课标的改革下，又创造了多种多样的新模式。随着对教学模式研究的不断深入，教师也更加明确没有一种教学模式可以成为固定模板，可以通用于所有数学课。因为每一堂课都有自身的特点，以“三角形的内角和”为例，打造了属于这堂课的“RPR教学模式”。第一步，通过逻辑推理，推导出直角三角形的内角和是180°；第二步，通过动手操作的环节，验证锐角三角形和钝角三角形的内角和是180°；第三步，通过课外知识的拓展——法国数学家帕斯卡的发现，再次用逻辑推理法巩固三角形的内角和就是180°。

关键词：教学模式；推理；实践；三角形；内角和

一、背景分析

中小学的教材中均有“三角形内角和定理”，即“三角形的内角和是180°”。《义务教育数学课程标准（2011年版）》在第二学段4～6年级图形的认识中，对“三角形的内角和”提出了这样的目标：“通过观察、操作，了解三角形内角和是180°。”而在第三学段7～9年级图形的性质中，提出的教学目标是：“探索并证明三角形的内角和定理。”显然，“了解”和“证明”是有区别的。了解是指能够从具体实例中知道或能够举例说明“三角形内角和是180°”的特征，而证明则要根据确实的材料判明“三角形内角和是180°”的真实性。

基于新课标对不同学段的不同目标，在教学设计过程中，就要依据教学目标来完成课堂教学。在小学阶段，需要学生了解这一规律，但并非是直接告诉学生结论，而是通过学生猜想、观察、操作等数学方法，发现三角形的内角和是180°。

二、教材分析

何为教材，顾名思义，即教学材料。教材是完成教学任务的依据，是教学过程的支架。为了上好“三角形的内角和”这一堂课，笔者横向比较了苏教版、北师大版和人教版三种版本的教材。

通过对三种版本教材的剖析，笔者有以下几点思考：

第一，更倾向于北师大版和人教版的安排，对于三角形的内角和，学生最基础的探究方法是量一量、算一算，但在苏教版中并无体现。但苏教版有一个知识点是其他版本不具备的，即导入时，有理论知识的铺垫，可以让学生更快进入角色。

第二，北师大版的引入比较卡通化，符合学生的认知结构，人教版的设计比较直接。相对而言，北师大版的探究方法更具多样性。

第三，三种版本都同样重视“拼一拼”的探究方法，其实这不仅仅是一种方法，更是一种转化思想的渗透。

通过教材对比以及对其他课辅材料的深入研究，确定本次教学重点是探索和发现三角形的内角和是180°，并能利用这一知识去解决相关问题。而难点是如何去证明三角形的内角和是180°，主要依据浙师大版的探究方法。

三、“RPR教学模式”的构建

（一）理论依据

研究表明，10岁孩子的左右大脑前额皮层发育完善，孩子的天性开始消退；相反，大脑抑制能力加强；思维能力的发展处在转折期，推理能力开始形成；培养思维的独立性和发散性在四年级尤为关键。所以在这节课的设计上，我特意设计了两次逻辑推理的环节，有意识地培养孩子的思维以及推理能力。

（二）模式构建

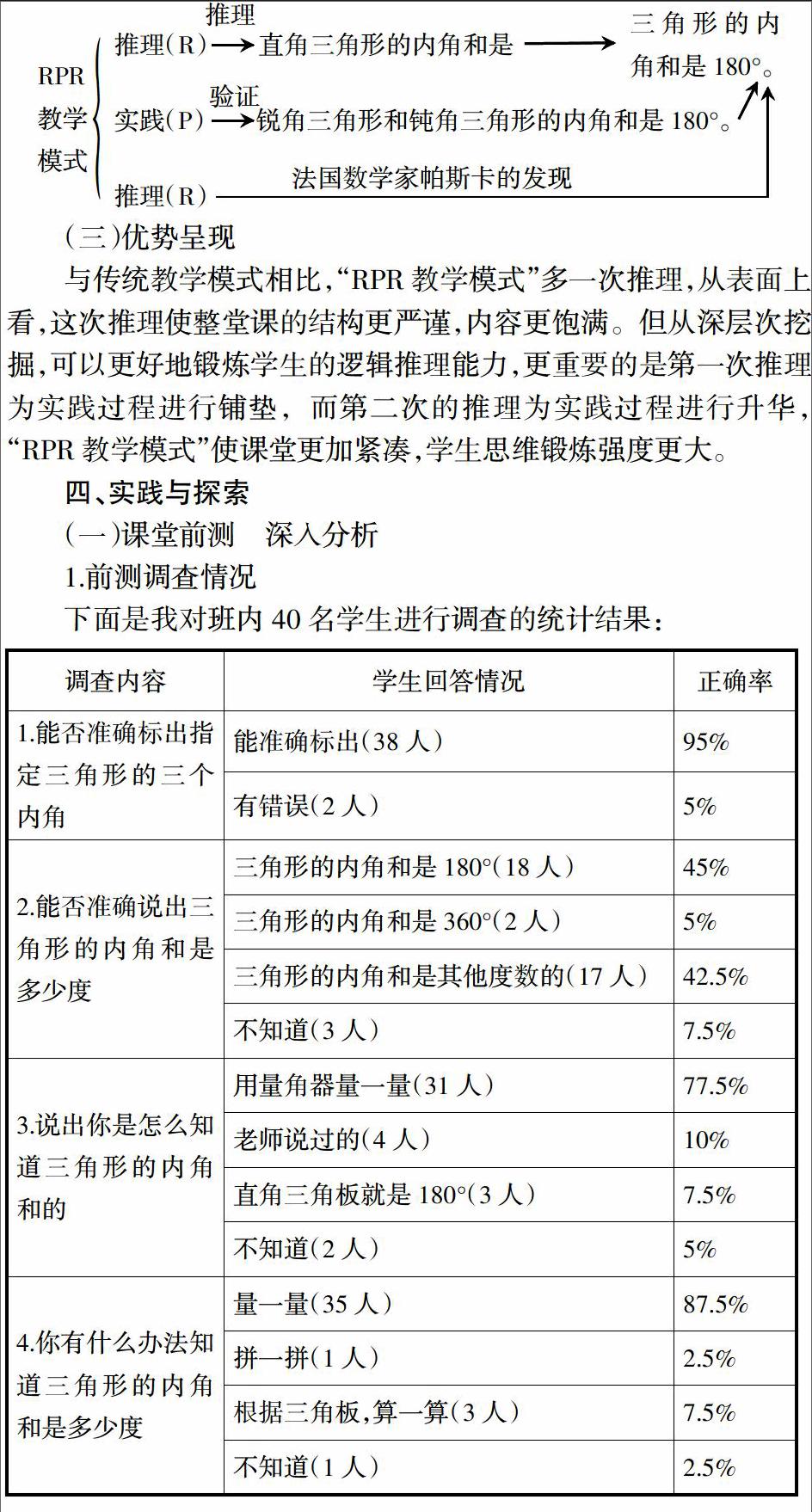
“三角形的内角和”采用了新的教学模式，比上面两种情况更为科学严谨——“RPR教学模式”。到底什么是“RPR教学模式”？即Reasoning（推理）—Practice（实践）—Reasoning（推理）三部曲。如图所示：

（三）优势呈现

与传统教学模式相比，“RPR教学模式”多一次推理，从表面上看，这次推理使整堂课的结构更严谨，内容更饱满。但从深层次挖掘，可以更好地锻炼学生的逻辑推理能力，更重要的是第一次推理为实践过程进行铺垫，而第二次的推理为实践过程进行升华，“RPR教学模式”使课堂更加紧凑，学生思维锻炼强度更大。

四、实践与探索

（一）课堂前测 深入分析

1.前测调查情况

下面是我对班内40名学生进行调查的统计结果：

2.调查结果分析

通过前测，我了解到以下三点：

第一，“三角形的内角”虽然是一个新的概念，但是通过已有的知识经验，95%的学生已经能够准确表达，所以在设计教学过程时，老师只需用一句话带过。

第二，三角形的内角和是180°，全班有45%的学生能够准确说出来，而42.5%的学生却说出了其他答案。通过分析，主要原因是题目1中有一个具体的三角形，大部分学生都想到了用量角器去量一量，由于不可避免的误差，以致学生回答出了五花八门的内角和度数。说明在众多的验证方法中，量一量的方法是最基础的。基于学生的回答，在进行教学设计的时候，我把测量的方法放在了最前面。

第三，除了测量和根据三角板计算的方法，还有学生想到了拼一拼的方法，看看是不是一个平角，能够想到这个方法，学生的思维算是比较活跃的。所以在进行教学设计时，我先把问题抛给学生，除了测量的方法，你还有其他办法来验证吗？

（二）教学初试 产生困惑

1.发现问题

（1）巧妙设疑，揭示课题

在导入部分，我设计了以下六个问题：

①出示长方形，问这是什么？（长方形）

②你们还记得长方形有几个角吗？（4个）

③每个角是多少度？（90°）

④所以长方形的内角和是？（360°）

⑤课件演示，将长方形对角线等分，所得图形的内角和是多少度？（180°）

⑥再继续等分呢？

此时学生的思维产生碰撞，有的学生认为是90°，也有的学生说还是180°，然后揭题，今天我们就来探究“三角形的内角和”。

（2）操作交流，探究知识

①初步猜想

让学生拿出自己的三角板，经历算一算，拼一拼更大的三角形等过程，猜想三角形的内角和是多少度。

②测量验证

师：怎样验证三角形的内角和到底是不是180°呢？你们有什么好办法吗？

生：量一量。

现在每个小组都有形状不同的3个三角形。请小组合作，完成活动记录表。

学生反馈测量的结果，并说说你发现了什么？

教学片段一：

师：通过测量，你发现了什么？（三角形的内角和有180°，也有不是180°）

师：请你观察这些内角和不是180°的，你发现他们都和180°很？（接近）

师：对呀，其实三角形的内角和是180°，只是测量的时候会出现？（偏差）

师：是的。不同的量角器会有误差，测量的时候也有误差，如一个80°的内角，有同学量出来是80°，有同学量出来是81°，所以测量结果并非十分精确。现在你知道三角形的内角和是多少度吗？（可能是180°，或者接近180°。）

学生的答案让我很诧异，不是已经很清楚地说明了测量时是有误差的吗？答案的呈现不应该是齐刷刷的一句“三角形的内角和是180°”吗？但还是有学生说“接近180°”，确实结果是学生自己亲自动手测量的，所以对于自己测量出来的答案早已根深蒂固，对于误差，学生还是不太能接受。

③拼接验证

师：同学们，刚才我们测量的过程中，由于误差的存在，并不能说不是所有的三角形内角和都是180°，那你还有其他办法吗？

请小组交流合作，请生汇报。

④课外拓展

法国数学家帕斯卡的发现。

2.引发深思

通过第一次的教学，我有了以下几点思考：

首先，在导入部分，我故意设计一个“圈套”，让学生产生困惑，当学生的思维产生碰撞时，让学生动手操作，经历探究过程去寻找答案。由于课前做过前测，知道大部分学生都会想到测量的方法，所以课前准备好三个三角形，钝角三角形、直角三角形和锐角三角形各一个，让学生来量一量，在量之前，一定要着重强调操作的规范性。反馈的时候，跟我预设的一样，有180°的，也有接近180°的，

课后，我一直在思考，怎样才能更好地解决误差这个问题。是否应该在操作前给学生一些暗示？但又不能直接告诉他们，这让我对本节课产生了新的困惑。

（三）挖掘教材 解决问题

1.初次推理

当我再次翻阅教本时，我发现练习十四中的第12题的第（2）小题，求长方形和正方形的内角和，这道题目对于学生而言，即使没有学过三角形的内角和，也是会求的，因为长方形和正方形的内角都是直角，90°×4=360°，但是教本的思路肯定是让学生分割成两个三角形，然后180°×2=360°。突然脑海中蹦出一个想法，既然已知三角形的内角和就能求长方形和正方形的内角和，那如果知道长方形的内角和，岂不是能将它分割成两个直角三角形，也能推出直角三角形的内角和？而且在我的教学设计中，本来就是用长方形导入的，如果能用长方形来推出直角三角形的内角和是180°，教学环节更加紧扣，而且让学生的探究过程更加充实，多了一种探究方法。更重要的是这样的探究方法是没有任何误差的。所以在第二次的教学过程中，我改变了教学过程，让学生先用逻辑推理法，得到直角三角形的内角和是180°。

例如，12.（1）用线段分别连接长方形、正方形一组对角的顶点，分别把长方形、正方形分成了两个什么图形？

（2）长方形和正方形的内角和各是多少度？

教学片段二：

课件出示各种形状的长方形和正方形：

师：同学们，今天老师请来了我们的老朋友，它们是？（长方形和正方形）

师：你们还记得长方形和正方形有几个角吗？（4个）

师：很好，我们就把这四个角称之为“内角”，那你们知道长方形和正方形的内角和是多少度吗？（360°）

师：你是怎么知道的？（一个内角是90°，4个内角就是90°×4=360°）

师：是不是所有的长方形和正方形的内角和都是360°呢？

（是的）

课件演示将所有正方形和长方形等分，变成

师：看，老师将它等分，现在我们得到了什么？（直角三角形）

师：那直角三角形内角和是多少度呢？（180°）

师：你是怎么知道的？（长方形和正方形的内角和是360°，进行等分后，就是360÷2=180°）

师：那这5个直角三角形的内角和都是180°吗？（是的）

课件演示 变成

师：好，老师将这个由正方形等分所得到的直角三角形继续等分，我们又得到了什么？（更小的直角三角形）

师：那你知道这个直角三角形，它的内角和是多少度吗？为什么？

生1：90°，因为180°÷2=90°。

生2：还是180°。上面的角和下面的角都是直角等分的，所以都是45°，45°+45°+90°=180°。

师：你听明白了？谁能再来说一遍。

师：如果老师将这个直角三角形继续等分，请问它的内角和是多少度？（还是180°）

课件呈现大小不一、形状不同的直角三角形。

师：通过推导，你现在知道大屏幕上的直角三角形内角和都是？（180°）

师：因为它们都可以由长方形或者正方形？（等分得到）

通过逻辑推理法，学生很好地推出直角三角形的内角和就是180°，没有任何误差。此时再来猜测锐角三角形和钝角三角形的内角和是多少度时，学生的心中已经潜意识地认识到锐角三角形和钝角三角形的内角和也是180°。当然，在学生动手操作的时候还是应该着重强调操作要求，本着科学严谨的态度进行操作，不得凑数，不得弄虚作假。不可否认，测量出来的结果还是会有误差存在，但是因为有了直角三角形的内角和是180°的铺垫，再向学生解释内角和接近180°，是因为误差的存在，学生显得更难接受。

2.动手实践

教学片段三：

师：同学们，刚才我们测量的过程中，由于误差的存在，并不能说不是所有的三角形内角和都是180°，那你还有其他办法吗？

师：同学们，那现在老师给你们一点小小的提示，好吗？请你想想看，我们能不能试着将这三个内角放到一块去呢？

请小组交流合作，请生汇报。

为了使探究方法多样化，除了量一量的方法，我们还应该灌输给学生一种转化的思想，将这三个内角转换为一个平角，即三角形的内角和就是180°。最后通过老师的指导，学生呈现了以下三种方法。

3.再次推理

其实早在300多年前，帕斯卡就已经发现了一种“0误差”的逻辑推理法去验证三角形的内角和，在前面两个环节的铺垫下，再进行课外知识的拓展。对于直角三角形的推导我们已经掌握了，主要是在锐角三角形、钝角三角形内做高，推出锐角三角形、钝角三角形的内角和是180°，虽有一定的难度，但是前面的铺垫够扎实，学生学起来就不那么费劲了。

五、教学体会

通过本次教学，笔者有以下几点思考。

（一）培养学生的综合能力

RPR教学模式中，三部曲的每一个环节都在努力培养学生的能力，第一步，逻辑推理法，顺利推导出直角三角形的内角和是180°。第二步，测量法，通过量一量，推出锐角三角形和钝角三角形的内角和是180°，并且运用转化的思想，把三个角放在一起，转化成一个平角，同样推出三角形的内角和是180°。在整个过程中，学生的动手能力得到了锻炼。第三步，进行课外知识的拓展，即法国数学家帕斯卡的发现。整个探究过程，收放自如，也提供给了学生较大的自我发挥的空间，较好地锻炼了学生的思维能力。

（二）开启新教学模式

推理、实践、再推理的教学模式并非通用于所有数学课，但是在动手实践的课堂上，这样的过程还是非常扎实的。如果没有理论知识的铺垫，学生直接动手操作，可能会有一定的盲目性，所以最好有一定的理论知识的灌输，然后再动手实践，但是往往实践的过程是有误差存在的，所以再一次用理论知识进行分析，最终获得结论。通过这样的三部曲，所得到的知识在学生心中将更加根深蒂固。

（三）推广应用

本次探讨是以“三角形的内角和”为例的，而“RPR的教学模式”既然是一种模式，自然可以推广应用。虽然它不能适用于所有的课堂，但是图形几何方面的课堂还是非常值得研究和探讨的，例如“平行四边形的面积”“多边形的内角和”等等。新的教学模式，自然有不成熟的地方，这需要慢慢磨炼，步步完善。

参考文献：

张苾菁.从实践操作到思想点化：《三角形的内角和》教学有感[J].小学教育教学，2011（04）.

编辑 李建军