基于相关分析的点磨削表面形貌均化特性研究*
2015-11-27邢春生邓延生王雨时修世超
邢春生 孟 竹 邓延生 王雨时 修世超
基于相关分析的点磨削表面形貌均化特性研究*
邢春生 孟 竹 邓延生 王雨时 修世超
(东北大学机械工程与自动化学院 沈阳110819)
机械零件的表面形貌对零件的工作性能以及使用寿命等有很大的影响。应用随机过程的相关分析,利用互相关函数对点磨削试件的表面形貌均化特性进行研究,并分析了点磨削加工对零件表面形貌的影响。研究表明:点磨削加工的零件表面截面轮廓波动平均间距较小,波纹细密性较高;点磨削变量角对零件的表面形貌有显著影响;点磨削加工能够显著提高零件表面形貌的均化特性。
表面形貌 相关分析 点磨削 均化特性
相关分析主要是指对两个以上具有相关性的变量进行定量分析,从而衡量两个变量之间的密切程度的方法,通过相关函数来分析零件表面的微观形貌,既能够反映工件表面截面轮廓的复杂程度,又可以说明其全部的形状特性。在此基础上,结合相关系数值的确定,能够更好的明确工件不同表面截面轮廓之间的相关程度,深入了解零件表面形貌的特征[1-3]。
点磨削是磨削技术中一种集CBN超硬磨料砂轮、数控技术和高速磨削技术于一身的新型磨削加工工艺,可以获得较高的加工精度和很小的表面粗糙度值,由于点磨削纹理与前道切削纹理存在交叉角度,形成了具有多尺度切削与磨削交叉纹理的微观几何特征。因此点磨削形成的工件表面形貌具有区别于普通磨削形成的工件表面形貌的纹理特征[4-5],表面纹理均化特性较好,工件表面的接触特性与摩擦学特性也不同于普通磨削表面。
本文利用相关分析方法对点磨削零件的表面形貌的均化特性进行分析,对于研究点磨削表面的接触与摩擦学特性具有重要意义。
1 点磨削加工参数对表面纹理特征的影响
点磨削主要用于轴类零件的加工,由于砂轮与工件之间存在点磨削变量角,表面磨削纹理的方向随着点磨削变量角的变化而变化,图1为点磨削加工的几何特征模型。
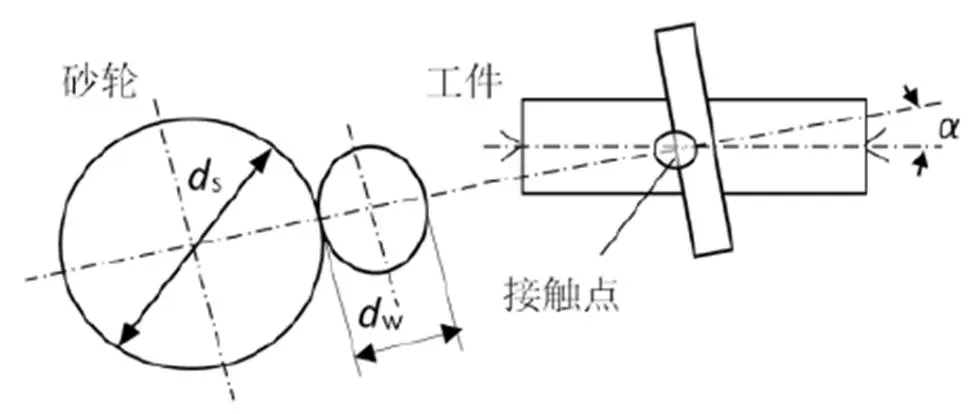
图1 点磨削加工几何特征模型
根据点磨削加工几何特征模型建立点磨削加工零件表面纹理方向模型,如图2所示。
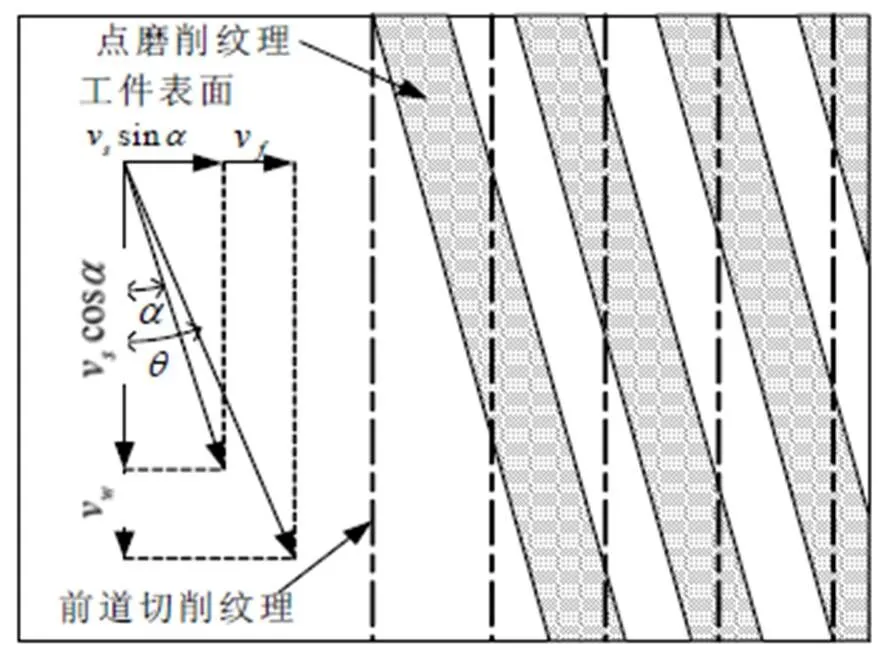
图2 点磨削表面纹理方向
图2中阴影部分为点磨削纹理,虚线为前道切削纹理。砂轮线速度为v,其轴向与径向速度分量分别为vsin和vcos,工件线速度为v,轴向进给速度为v方向如图2中所示。根据速度矢量合成原理,工件表面点磨削纹理方向角的表达式为:

式中,“+”用于顺磨,“-”用于逆磨。点磨削工件表面的纹理方向由砂轮线速度v、工件线速度v以及工件轴向进给速度v三个速度矢量合成得到。点磨削加工常采用逆磨方式,表面纹理方向角将随v和v增大而增大。在点磨削条件下,工件速度v和轴向进给速度v远小于砂轮线速度v,因此点磨削变量角是影响点磨削表面纹理方向的主要因素。
2 零件表面形貌相关分析
2.1 互相关函数
如图3所示,互相关函数用于零件表面形貌的识别,主要是从定量分析的角度表达零件的两个表面截面轮廓模型之间的相似程度,即表示一个没有位移和一个有横向位移的不同表面截面轮廓曲线位移间隔为的相似性。

图3 互相关函数
互相关函数的表达式为[6]:

式中为沿表面截面轮廓的距离;为横向位移;为评定长度。
互相关函数的数字化估计公式为[7]:
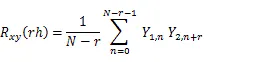

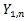
2.2 互相关系数
相关本身并不是一种确定性的关系,相关函数一般只能描述两表面截面轮廓的相似性,而相关程度则通常由相关系数值来表述。相关系数是一个无量纲的量,其中,互相关系数能够反映两个不同表面截面轮廓的相关性。用R()表示互相关函数值,R(0)和R(0)则表示在=0时两个不同的表面截面轮廓的自相关函数值,则互相关系数可由如下计算表达式得到

对于给定的值,互相关系数的具体分类条件如表1所示:

表1 相关程度的界定范围
3 点磨削表面形貌实验研究
3.1 实验原理及试件制作
为增大工件表面纹理的尺度,以便清晰地表述具有点磨削加工表面纹理特征的试件表面特征,试件采用先切削后磨削的方法加工制作。在试件的加工过程中,需要调整砂轮的线速度方向,使砂轮线速度方向与前道切削纹理方向形成符合最终表面要求的夹角,即所形成试件的表面纹理是由较大切深的切削纹理和带有点磨削变量角的小切深磨削纹理叠加而成。其三维表面形貌示意图如图4所示,较大的切深纹理为前道切削加工形成,较小切深纹理为点磨削加工形成。

图4 试件三维表面形貌示意图
具体的加工实验方案如表2所示,每个试件的磨削纹理的方向不同,与前道切削纹理的夹角分别为10°、20°、30°,试件分别编号为1号、2号、3号试件,加工后的试件实物如图5所示。
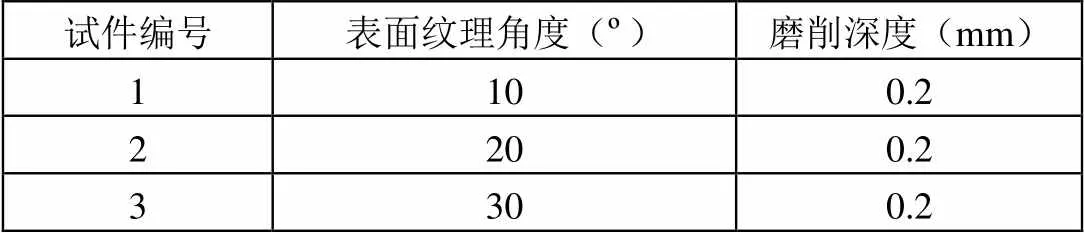
表2 实验加工方案设置

图5 实验用试件(不同纹理方向)
3.2 试件表面截面轮廓曲线提取
采用TR300触针式粗糙度形状测量仪对每个试件分别在垂直、平行于前道切削纹理方向,垂直、平行于点磨削纹理方向的四个方向测量,共计得到12组数据。测量时将试件的取样长度设定为0.8 mm,评定长度为4.0 mm,得到的三个试件在平行于点磨削纹理方向的表面轮廓曲线如图6所示,其他方向的轮廓曲线不再重复给出。
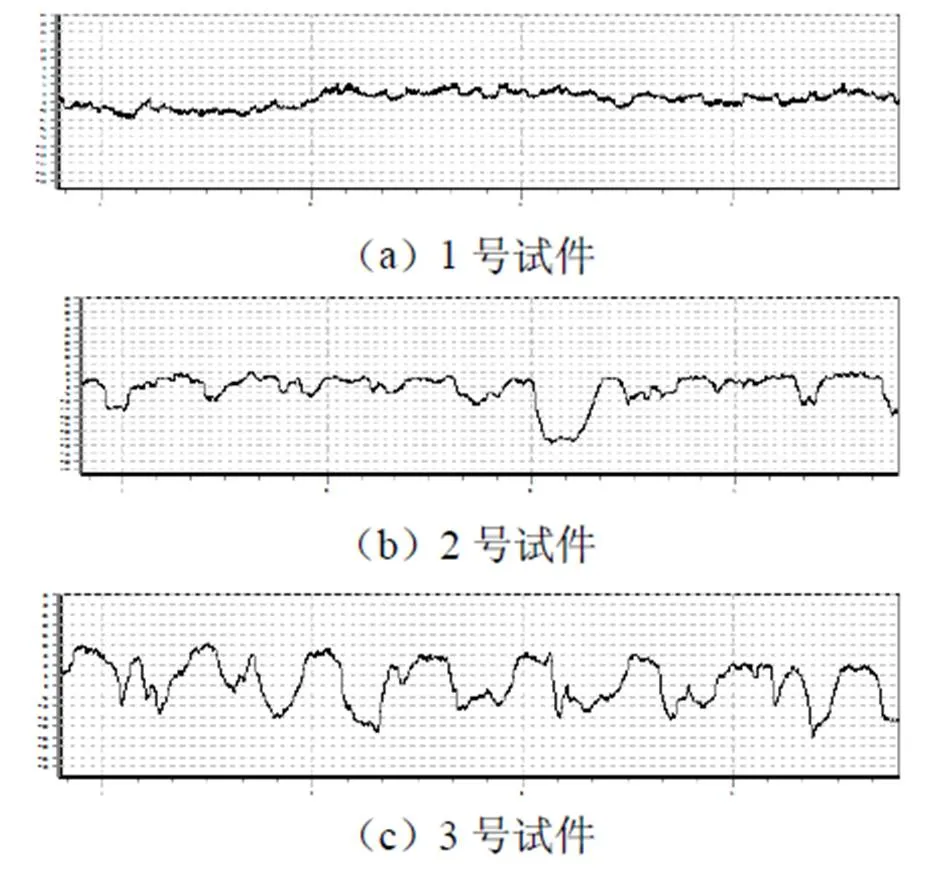
图6 三个试件的表面截面轮廓曲线示意图
(平行点磨削纹理方向)
3.3 对轮廓曲线进行互相关分析
测得轮廓曲线后,对轮廓曲线每隔8×10-3mm进行采样,得到大量的实测数据,将这些数据输入计算机处理,建立数学模型并结合Matlab软件,计算求解三个试件的相关函数曲线、相关函数值及相关系数值。图7为1号试件在四个方向上的表面截面轮廓曲线的互相关函数,其他试件的互相关函数不再重复给出。

表3给出了所有试件的四个表面截面轮廓之间的互相关函数和互相关系数,其中轮廓a、b、c、d分别代表的方向为:垂直前道切削纹理方向、平行前道切削纹理方向、垂直点磨削纹理方向、平行点磨削纹理方向。

表3 试件表面截面轮廓互相关函数和互相关系数
3.4 结果分析与讨论
结合图7和表3对点磨削表面形貌的特征进行分析讨论,得出如下结论:
(1)图7中,试件四个方向的表面截面轮廓之间的互相关函数均随着横向位移的增加出现不衰减的小周期特征,这从定性角度说明了试件在经过点磨削后,表面截面轮廓波动平均间距较小,波纹细密性较高。
(2)表3中,对比三个试件的6组互相关函数可以看出,3号试件的各个互相关函数的绝对值的最大值是三个试件中最大的,这说明了点磨削的加工纹理方向的改变,对零件的表面形貌特征具有显著影响,在工程上应针对具体情况选择合理的点磨削变量角,以达到较为合理的表面形貌特征。
(3)表3中,各个试件的互相关系数的绝对值的最大值均超过了0.6,有的甚至接近1,这从定量的角度充分说明了零件经点磨削后,各方向表面截面轮廓曲线都显著相关,表面纹理均匀一致,各向同性较好,具有均化特性。
点磨削加工表面形貌具有多尺度交叉纹理特征,表面截面轮廓的波动较小,纹理均化特性较好,区别于普通磨削形成的工件表面形貌,因此,点磨削工件表面的接触特性与摩擦学特性也不同于普通磨削表面,研究点磨削表面形貌的均化特性对提高零件表面的接触与摩擦学特性具有重要的指导意义。
4 结语
(1)点磨削表面截面轮廓波动平均间距较小,波纹细密性高,具有较高的加工精度。
(2)点磨削变量角对零件的表面形貌特征具有显著的影响,应针对具体的工况选择最优的点磨削变量角。
(3)零件表面经点磨削后,各方向的表面截面轮廓曲线都显著相关,各向同性较好,具有均化特性。
[1] 邢彦锋,张明,侯仰海.电化学机械光整加工表面相关性分析[J].山东理工大学学报(自然科学版),2003,17(3):23-26.
[2] 李长河.砂轮约束磨粒喷射精密光整加工机理及表面特性的研究[D],沈阳:东北大学,2006.
[3] 李西琴,陈历喜,汪慰军.用互相关函数判别零件表面形貌的特征[J].机械科学与技术,1998,17(1):49-53.
[4] Xiu S C, Cai G Q, Li C H.Study on surface finish mechanism in quick-point grinding[J].IJCAT,2007,29:403-408.
[5] 晁彩霞,王洪远,孔年香等.点磨削纹理特征及对零件摩擦学性能的影响[J].润滑与密封,2014,39(9):4-7.
[6] 张洪亭,高德福.测试技术[M].沈阳:东北大学出版社,1996.
[7] 吴正毅.测试技术与测试信号处理[M].北京:清华大学出版社,1989.
*国家自然科学基金资助项目
编号:51075065
