一种提高振动源扫描算法信噪比的方法

刘双庆，谢 静，王熠熙

（天津市地震局，天津 300201）

0 引言

对产生信号的信号源进行有效定位，是被动式观测系统研究的主要课题。当信号源周边散布多个监测仪器，由信号源同一时刻发出的信号到达各仪器存在较确切的初至时间时，可以利用相应的走时方程进行联合定位。在地震科学中，对地震震源位置进行定位即是其中的一个例子。传统的地震定位，需要较清晰的震相初至到时及明确的震相属性（Pg、Sg、Pn、P、PkP、PKIKP 等等），以便利用恰当的走时方程［1］。对于震相属性不明确，或初至到时不清晰的振动信号，对其产生源进行定位则较困难。为此，一些学者提出了反向投影算法。这种算法基于如下假定：从振动源发出的到达各接收点的信号，其时间序列上存在先后到达顺序。如果消除振动源到达各接收点的传播走时，则时间序列上的信号起始点将排列得很整齐。因此再将这些消除走时差异的信号叠加，将有较高的信噪比。这个高能量的信号即为各接收点反算出的震源点某时刻发出的振动。如果假定的震源点非真实震源位置，则到达各接收点的走时与实际走时不一致，消减这些走时后，各时间序列上的信号起始点排列仍不整齐，叠加后的信噪比较低。因此，在真实震源附近区域对某时刻反算出的信噪比进行成像，可以获得真实震源最可能的位置，即具有最高信噪比的点位。2011年日本MS9.0地震破裂过程反演中，不同频率的振动源强度分布特征研究就使用了反投影算法［2］。SSA（source－scanning algorithm）算法则是反投影算法中的一种计算实现模型，它引入“亮点函数”进行刻画［3］。由于在近场条件及较高频成分中，随着震中距离的改变，从同一震源发出的信号将出现拉长现象，直接矢量叠加效果较差。利用绝对值处理有明显改善，但是对振动型信号进行直接绝对值处理，会引入伪高频成分。其他学者还针对振动拉长现象进行非等间隔重采样处理，但改进效果不是很明显［4］。本文将利用局部极值特性，对地震数据构建较好的包络线，以该包络线作为SSA 计算的预处理数据，讨论这种处理方式的优点，并用白噪声检验其稳定性及其他特性。

1 振动源扫描（SSA）模型

1.1 常用的SSA模型

SSA 模型由Kao和Shan于2004年提出，是一种通过波形对震源分布进行定位成像的方法［5］。假设一个振动事件由N 个台站记录到（如图1 中的A、B、C三个台站），首先归一化每个台站的各通道记录值un，然后计算某个空间点η在τ时刻的亮度函数：

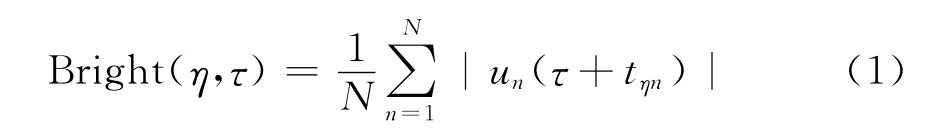
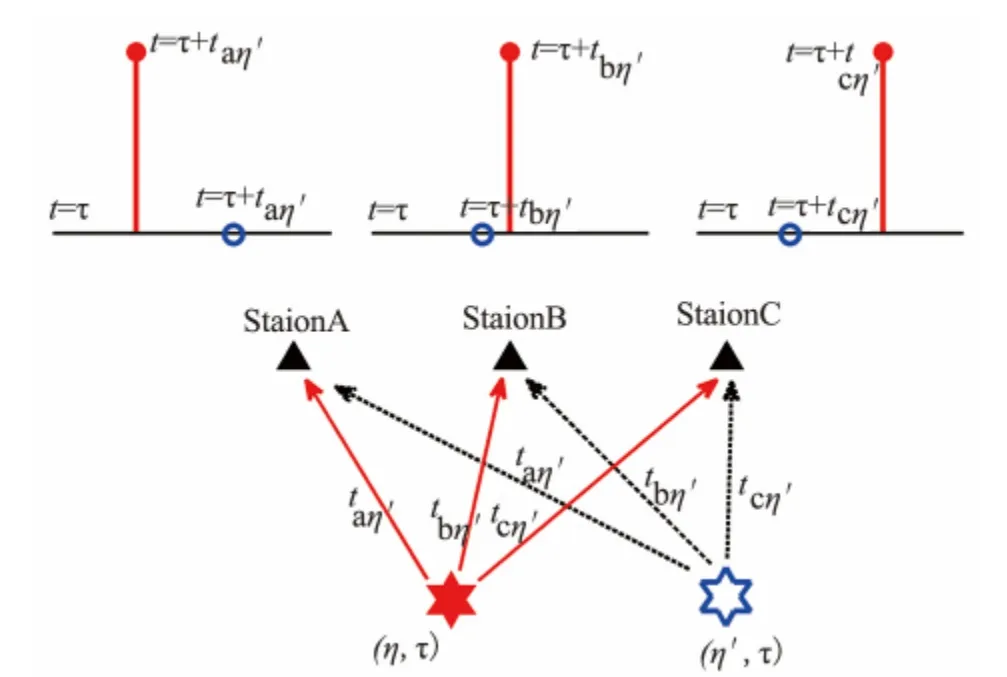
图1 振动源扫描算法原理示意图（据文献［3］修改）空间上的点η在τ时刻的“亮度”可以由相应台站的理论到时（即τ加上相应的走时taη、tbη、tcη）计算给出，如果某处“亮度”大（图中的实六角星），表明这里有事件发生，如果“亮度”小（空六角星），表示这里没有事件发生

式（1）中：un为归一化的地震记录，在本文中取垂直分量的直达震相波列进行分析；tηn为 从 点η到台站n计算的某个最大能量震相走时，如果所有的最大振幅都是由点η和时间τ产生，那么Bright（η，τ）＝1，即图1中红色脉冲都被刚好选择上。如果脉冲信号都没被选上，则Bright（η，τ）＝0，即图1中蓝色空心圈圈定位置。通常情况下，Bright（η，τ）既不等于1也不等于0。另外，由于区域速度模型跟真实地壳结构很难完全一样，为了抑制理论走时误差的影响，需对求和的N点数据进行高斯窗加权处理。

1.2 本文的改进模型

地震仪器记录的地震波列一般呈正负振荡衰减。按式（1）直接将小于0值的数据进行x轴对称翻转，则原在0点附近近似光滑的波形将不再可导，从而人为引入高频成分（图2b）。为此，本文将不直接对负值区振幅取绝对值，而是先拟合数据的包络线。最常用的包络线是对数据先进行等间隔处理，然后提取各间隔区内的最大或最小值作为该区间的代表值，连接这些值所获取的曲线作为原始数据的包络线。由于地震信号是一种非平稳时间序列过程，对间隔长度的不同选择，会对结果有较大影响，而且等间隔选择也不能突出局部非平稳性。鉴于这种情形，本文提出利用光滑后的局部极值特性进行包络线追踪拟合。此外在一般情况下，地震波列还含有环境噪声及地震仪器热噪声等随机干扰，因此，操作过程分以下4步。

（1）按分析的震相（或波列）主要周期段，先进行ButterWorth带通滤波，获取相对光滑的波形；

（2）对光滑后的数据求导，获取导数为0的时间轴点；

（3）按奇数或偶数脚标提取导数为0的时间点及相应的波形数据；

（4）对这些数据进行分段3次埃尔米特插值，获取数据包络线。其中两端无0值导数的数据段按滤波后的数据进行补充（图2a）。

经过上述处理后，再利用式（1）进行SSA 分析（本文所有算例都使用了高斯窗加权处理）。通过以上方式，可以较好地捕捉到原数据的局部极值，同时降低高频成分的引入。

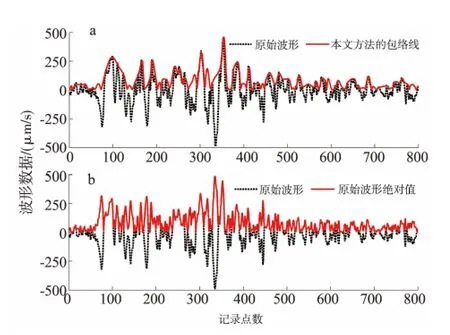
图2 对原始波形进行两种不同处理方式的结果对比

2 振动源事件的SSA 分析

2.1 有源地震震中定位

2014年9月6日18时37分在河北延怀盆地中发生了一次MS4.3 级地震，其震中定位结果为（115.433°E，40.278°N，深度约14km）。首都圈台网中大部分台站对这次地震都有较高的信噪比记录。本节利用该地震对本文的方法进行详细对比。其中，图3a是直接采用绝对值方法给出的结果；图3b为本文引入的方法的结果；图3c为直接使用原始波形进行SSA 扫描的结果，图中的三角形为参与扫描计算的台站。计算结果清晰显示，直接使用原始波形，亮度函数值有正负性，数值很低（0.001的量级）；用绝对值的方法，亮点函数的最大值约0.26；而本文所用方法提高到0.41左右。亮度函数值的空间分布上，本文给出的结果其边缘特征更显著。作者还对扫描求和的长度N 进行调整，其计算的结果相类似。但如果N 很大，比如大于振动时间长度的2倍，则分辨率较低；N 更长时，分辨率更低。N 宜取分析的台站中，95%振动能量持续的平均时间。

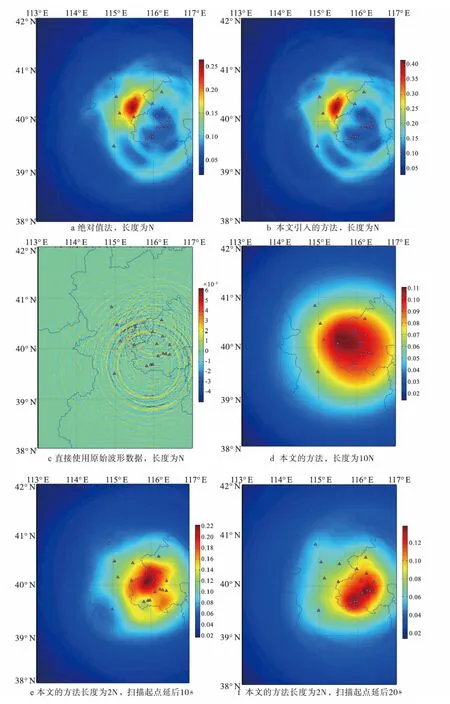
图3 对原始数据进行不同处理后获取的SSA 扫描图像

2.2 无源噪声定位

当存在有源信号时，只要信号发生时刻较准确，并且传播的介质速度模型比较合理，则利用绝对值法和本文的方法进行SSA 分析一般都能获取到信号源的有效位置。但是如果振动源产生的待研究信号的发生时刻未知，信号的信噪比也未明确给出时，对该信号的产生源进行定位则非常困难。因此，评价一个观测系统若干台仪器记录的信号中是否存在可探测的同源信息是一个棘手的难题。在此利用无源白噪声及SSA 算法进行分析，对其部分特征进行表达。无源噪声基础数据采用Matlab软件自带的rand函数进行生成［6］。所使用的仍是图3 中所示的台站，但每个台站的伪随机数生成种子并不相同，以保证各道的随机数列几乎完全互不相关。图4给出了直接利用均匀分布的伪随机分布噪声（图4a）、该噪声绝对值（图4b）、对该噪声处理的本文算法（图4c，扫描长度扩大为2倍）；以及利用噪声绝对值法，改变扫描长度扩大为原长度的2 倍、4 倍、10倍的效果（图4d～图4f）；改变扫描起始时间点10 s、20s后的效果（图4g、图4h）。其中N 为1 201点，如果采样率取100sps，则对应12s长度。

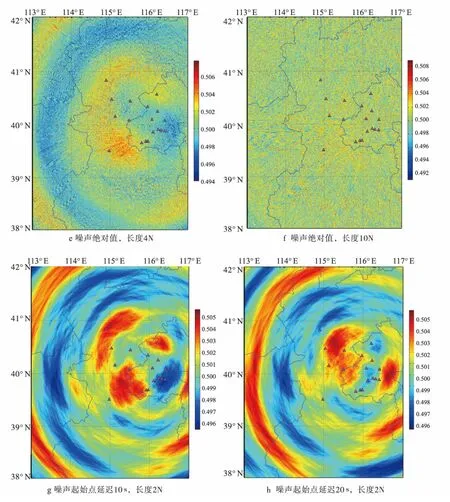
图4 利用均匀分布的噪声对不同扫描长度、起止时间、不同预处理方法的结果对比

通过图3和图4的结果对比，可以获得以下几点主要认识：

（1）当不存在发生源时，不同设置下所计算的亮度函数最大最小值差异都很小，一般在0.02左右。而有源存在时，亮度函数差异在0.2以上，两者相差一个量级。

（2）噪声信号计算出的亮度函数值在0.5左右。

（3）有源信号存在时，直接用绝对值处理的SSA 方法和本文包络线的SSA 方法，两种亮度函数的结果分布形态很相似。而噪声信号，两者的结果差异较大（图4c、图4d）。

（4）扫描长度N 的变化对噪声信号的结果影响更显著，当N 扩大10倍时，几乎显示不出N 未变化时的亮度函数分布特征。

（5）噪声起始点延迟或提前，亮度函数的空间分布近似以台站中心为汇聚或发散点进行汇聚或向外传播。其原因是延后扫描的起始点时间，相当于将噪声数据时间轴提前，因此亮度函数将向台站中心汇聚（图4d、图4g、图4h）。而对于有源信号，延后扫描点将导致只有部分台站能接收到由该源发出的波列的后半部分，而其他台站漏记，因此扫描出的亮点函数将向这些能接收到部分波列的台站中心汇聚（图3b、图3e、图3f）。即有源信号延迟扫描，亮度函数高值区呈有向性偏移。而随机信号以汇聚或发散为主要特征。

（6）扫描起始点偏移，对随机信号的亮点函数值影响不大，仍保持在0.5左右，而有源信号信噪比显著降低。

3 认识及讨论

本文利用局部极值构建地震仪记录的原始数据包络线，在此基础上对振动源扫描算法SSA 的信噪比进行分析。经地震事件扫描检验，本文给出的方法确实能提高SSA 的信噪比，最大值提高约1.6倍，而且亮度函数空间分布的边缘特征更清晰，有利于确定振动源位置。本文的SSA 扫描结果的高值区与地震编目的震中位置很吻合。经过多次测试显示：式（1）中的求和长度N 宜取分析的台站中，95%振动能量持续的平均时间。N 过短可能导致远台未接收到振动的主要能量，N 过长导致非源振动能量进入，且分辨率降低。

本文还对无源均匀噪声进行SSA 扫描，以研究其与有源信号的区别。计算显示，无源噪声扫描的亮度函数值在0.5附近，而且最大最小值差异很小，约0.02左右。而有源信号一般差异为0.2，二者相差一个量级。对有源信号扫描起点变动后，亮度函数的高值区呈方向性偏移，主要偏于能接收到该源部分信号的台站（网）中心。而无源信号扫描起点变动后，亮度函数表现为以台站（网）为中心而进行的发散或聚敛。而且有源信号的亮点函数值显著下降，但随机信号的亮度函数值未出现明显变化。随着扫描长度N 的增长，随机信号的亮度函数空间分布特征持续性较差。

当然，引起SSA 算法的信噪比变化的因素很多，其与信号源的自身特征也有很大的关系。本文从几个主要参数进行对比分析，虽然较清晰地展示了本文提出的方法的优点，以及对无源随机信号判别的一些特征，但对不同信噪比的有源信号的分析仍未进行展开，这是后续需要进一步强化的内容。

［1］ 国家地震局地球物理研究所.近震分析［M］.北京：地震出版社，1978：3－8.

［2］ 姚华建.用基于时间域和频率域的反投影算法研究大地震的破裂过程［R］.北京：中国地震局地震预测研究所学术报告，2013.

［3］ 李文军，李丽，陈棋福.用震源扫描算法（SSA）研究列车源的运动［J］.地球物理学报，2008，51（4）：1146－1151.

［4］ 张瑞红，林大超，乔兰.一种改进的震源扫描算法微震定位［J］.煤矿安全，2011，42（5）：48－51.

［5］ Honn Kao，Shao－ju Shan.The source－scanning algorithm：mapping the distribution of seismic sources in time and space［J］.Geophys.J.omt.，2004，157：589－594.

［6］ Cleve B.Moler.Numerical Computing with MATLAB［M］.America：Society for Industrial and Applied Mathematics，2004：255－264.