自动弹仓回转选弹动力学仿真及优化
2015-11-27魏继卿许耀峰刘小蒙解凤娟鲁玉祥
魏继卿,许耀峰,刘小蒙,解凤娟,鲁玉祥
(西北机电工程研究所,陕西 咸阳 712099)
现代大口径压制火炮为增大威力、减轻乘员工作强度和提高战场生存能力[1],多配备弹药自动装填系统,其中自动弹仓用于装卸、贮存和选择弹丸,并将其传递到弹协调器上[2]。某大口径火炮采用结构紧凑、传动效率高的链式回转弹仓,其链轮只有4个齿,弹筒链运动的多边形效应比较显著[3],导致弹仓运行不平稳,且滚轮在与链轮、导轨接触时存在冲击,对结构产生较大的作用力,造成能量的损耗。笔者采用RecurDyn软件对自动弹仓的回转选弹运动进行仿真分析,并探讨减小冲击的方法的可行性。
1 弹仓建模
1.1 几何建模
RecurDyn的几何建模功能较弱,并不适合复杂模型的构建,因此在UG 中建立自动弹仓的三维模型。建立动力学模型时,忽略一些不影响结构运动的细小特征,简化后的几何模型如图1所示。弹仓由主动链轮、从动链轮、导轨、贮弹筒、弹丸、滚轮和销轴等组成。弹丸在贮弹筒内有很好的固定,故将弹丸与贮弹筒也合并在一起[4]。贮弹筒之间通过销轴连接成弹筒链,滚轮套在销轴上,并与链轮、导轨接触。

1.2 动力学建模
几何建模完成后,输入各零件的质量、质心、转动惯量等属性。设置重力加速度方向为-y,大小为9.86m/s2。
根据各零部件的装配和运动关系,建立必要的约束关系:弹架(导轨)与大地以固定副连接;主从动链轮与大地均以转动副连接;贮弹筒与销轴、销轴与滚轮均以转动副连接;链轮与滚轮以实体接触连接;链轮与导轨以面接触连接。
RecurDyn通过检验几何外形来判断是否发生接触,基于Hertz接触理论计算接触力。接触产生的法向接触力

式中:k为接触刚度系数;c为接触阻尼系数;δ和分别为接触穿透深度及其导数;m1、m2、m3分别为刚度指数、阻尼指数及凹痕指数,用以描述接触的非线性[5]。这些参数的取值取决于相接触物体的材料、形状和尺寸。
1.3 仿真分析
根据实际情况,设定主动链轮角速度满足STEP(time,0,0,0.5,1),即0.5s 内加速到1 rad/s,之后保持匀速。设置仿真时间为7s,这样链轮可以转一圈,能够较好地观察弹仓选弹过程。设置完成后,即可进行仿真计算。
2 仿真结果分析
仿真结束后,计算出的机构运动过程表明,自动弹仓的运动符合实际情况。
图2为从动链轮角速度随时间变化的曲线。0.5s后,曲线围绕1rad/s周期性波动,波动范围为0.707~1.376rad/s,波动周期约等于弹筒平移一个弹距(链轮转动1/4 圈)的时间π/2s,这正是多边形效应的体现。图3所示为主从动链轮转角差变化曲线,转角差围绕0°在-1.840°~1.822°间周期性波动,说明主从动链轮的转动并不同步。贮弹筒平动的线速度也围绕其理论值周期性波动,曲线形状类似从动链轮角速度,运动并不平稳。贮弹筒时刻都处在变速的过程中,因而各贮弹筒之间的作用力也不会保持恒定。

图4展示了链轮与滚轮接触力的变化。两者接触的时间为0.85-4.35s,接触力曲线出现4个波峰,最大值达到11.44kN。接触力不恒定,是由贮弹筒之间作用力不恒定造成的。
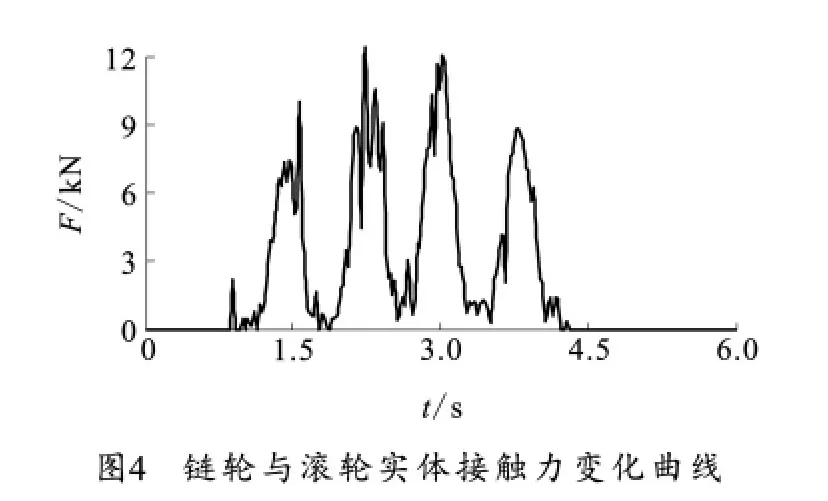
图5展示了滚轮与中导轨接触力y向分量的变化情况。所连接的两贮弹筒均做平动时,由于重力,滚轮只与下导轨接触,中导轨接触力为0;当滚轮前面的贮弹筒开始绕主动链轮转动而后面的贮弹筒依旧平动时,在贮弹筒之间的作用力y向分量作用下,滚轮开始与中导轨接触;随着转角变大,作用力y向分量变大使接触力逐渐变大,最大值为3.758kN;而后滚轮开始与链轮接触,链轮对其的作用力使其与中导轨的接触力变小,直至滚轮脱离导轨,接触力变为0。接触力的变化反映了平动到转动变化过程中的冲击。接触力非0 的时段为1.95-2.50s,这段时间滚轮沿导轨平移了约60mm。

图6展示了主动链轮驱动扭矩的变化情况。在大部分时间驱动扭矩都处在±300N·m 的范围内,发生冲击时会瞬时达到±500N·m。冲击往往发生在滚轮与链轮、导轨的接触和分离时,对弹仓的结构、驱动电机等都是不利的,须设法减小其作用。

3 改进设计的仿真结果分析
3.1 改进导轨设计
模型中上导轨和下导轨起支撑和引导作用,中导轨只起引导作用,约束滚轮使弹筒链的运动符合要求。由图5可知,在贮弹筒由平动变为转动时,中导轨端部限制了滚轮的运动,产生了接触力的冲击。考虑冲击影响的范围,将中导轨左右各缩短60mm。
弹仓运转并未受到导轨缩短的影响。结果表明,速度变化较小,力的变化较大。滚轮与中导轨的接触力变为0,冲击消失,改善了滚轮和导轨的受力状况。
图7展示了改进后链轮与滚轮接触力变化情况。尖峰变为2个,最大值减小为10.652kN。缩短导轨减少了弹筒链运动的约束,因而能改善接触力。

图8为改进后的主动链轮驱动扭矩变化曲线。扭矩最大值减小到±400N·m,且发生冲击的时刻较改进前有所减少。这说明缩短导轨能有效减少冲击,改善弹仓的受力和电机的负载。

3.2 改变链轮连接方式
原模型中链轮与大地以转动副连接,这是一种理想的刚性约束关系,约束的自由度上不能有相对运动。柔性连接考虑了变形的因素,用与两构件相对位移和速度成正比的力阻碍其相对运动。
将从动链轮与大地之间的转动副改为衬套力[6](RecurDyn中的一种柔性连接方式),表现在结构上即将链轮安装座通过可滑动的弹性调节装置与弹架连接,使其可根据受力状况自动调节链轮中心距。
再次仿真后,弹仓运行依旧平稳;链轮与滚轮实体接触力峰值减小为2.448kN;滚轮与中导轨的接触力峰值减小为0.269kN,力的冲击大大减小。
图9为改进后的主动链轮驱动扭矩变化曲线。扭矩最大值减小到±200N·m,说明改变链轮连接方式能有效减少冲击和功率损耗。
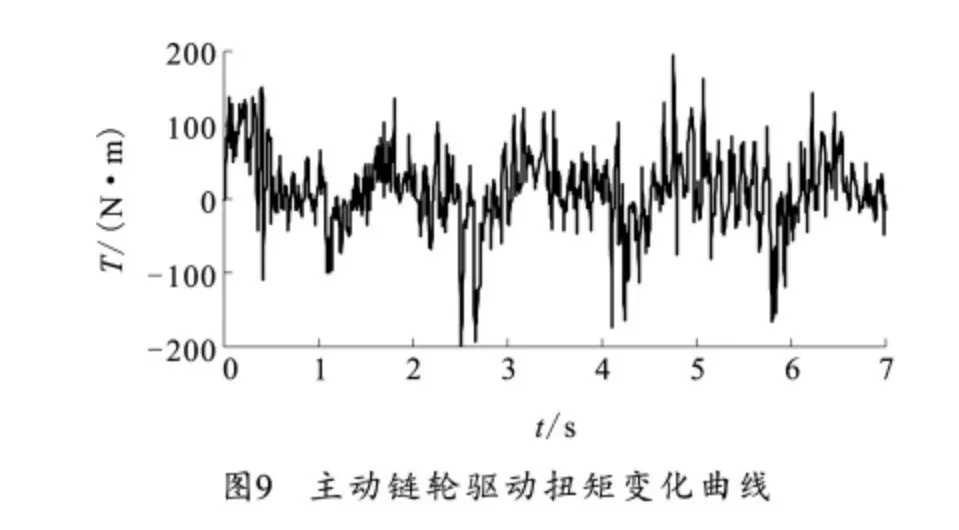
图10展示了从动链轮x方向位移的变化曲线,可以看出,链轮向右的位移周期性波动,峰值为0.377mm。这表明原来的模型弹筒链过紧,张紧力过大,柔性连接可使其适当松弛。

无论是缩短导轨长度,还是将链轮与大地柔性连接,本质上都是减少结构上对弹筒链运动的限制性约束,缓解弹筒链过紧,从而减少力的冲击和功率的损耗。
4 结论
笔者用RecurDyn软件对自动弹仓选弹运动进行了仿真,分析了运动参数和受力的变化情况,表明从动链轮和贮弹筒的速度存在周期性波动,滚轮与导轨、链轮的接触存在冲击;改进导轨和链轮连接方式,可减小冲击的作用和功率的损耗,改善弹仓受力状况,此结论对改进弹仓设计起到一定指导性作用。
(References)
[1]赵抢抢.弹药自动装填系统可靠性初步研究[D].南京:南京理工大学,2013.ZHAO Qiangqiang.Initial research on the reliability of the automatic ramming organ system[D].Nanjing:Nanjing University of Science and Technology,2013.(in Chinese)
[2]侯保林,樵军谋,刘琮敏.火炮自动装填[M].北京:兵器工业出版社,2010:217-218.HOU Baolin,QIAO Junmou,LIU Congmin.Automatic gun feeding[M].Beijing:Publishing House of Ordnance Industry,2010:217-218.(in Chinese)
[3]解凤娟,何宗颖,骆小平,等.基于RecurDyn的链式回转弹仓多边形效应分析[J].火炮发射与控制学报,2013(2):27-28.XIE Fengjuan,HE Zongying,LUO Xiaoping,et al.Analysis of the chain type turns round magazine polygon effect based on RecurDyn[J].Journal of Gun Launch &Control,2013(2):27-28.(in Chinese)
[4]曾军令.齿形链在火炮弹药自动装填系统中的应用研究[D].南京:南京理工大学,2011.ZENG Junling.Research on the application of silent chain in the artillery’s ammunition automatic loading system[D].Nanjing:Nanjing University of Science and Technology,2011.(in Chinese)
[5]刘义.RecurDyn 多体动力学仿真基础应用与提高[M].北京:电子工业出版社,2013:296-297.LIU Yi.RecurDyn multi-body dynamics simulation basic application and improvement[M].Beijing:Publishing House of Electronics Industry,2013:296-297.(in Chinese)
[6]焦晓娟,张湝渭,彭斌彬.RecurDyn多体系统优化仿真技术[M].北京:清华大学出版社,2010:136-137.JIAO Xiaojuan,ZHANG Xiewei,PENG Binbin.RecurDyn technology of multi-body system’s optimization and simulation[M].Beijing:Tsinghua University Press,2010:136-137.(in Chinese)
