基于中国出行特性的公交站距多目标优化模型

刘昕嵘,苏玮辰

(南京城建项目建设管理有限公司,江苏 南京 210000)

基于中国出行特性的公交站距多目标优化模型

刘昕嵘,苏玮辰

(南京城建项目建设管理有限公司,江苏 南京 210000)

为了更好地研究中国的最优公交站间距、揭示不同公交站距对乘客出行及公交系统服务的影响,评价公交站距对平均乘客出行时间、单程公交总运行时间及公交服务区域的影响,建立了一个多目标优化模型。用修正的向量评估遗传算法(MVEGA)和基于遗传算法的模型转化法求解该模型。研究结果表明:MVEGA法的结果要优于模型转化法的。由敏感性分析可知,最优公交站距对平均出行距离和最大步行距离更加敏感。对南京市11路公交的数据进行了实测,得到该线路的最优公交站距(690 m)。选择出行距离分布函数来表征出行距离的变化,研究站距对乘客出行和公交系统运行时间的影响,将公交服务的覆盖引人模型。

公交站距;多目标优化;出行距离;出行时间;遗传算法

公交站点的数量和间距是公交系统一项十分重要的评价指标,也是影响乘客乘车便利程度、车辆运营速度和公交运营调度计划的重要因素[1]。它影响着公交车辆的运营速度、线路的发车间隔、配车数及线路运载能力。优化公交站点的站距能有效提高公交系统的性能。近年来,学者们从2个方面对公交停靠站最优站距进行研究:①从乘客的角度出发,研究单个乘客或者乘客平均公交出行时间,使乘客公交出行的消耗最小,吸引更多的乘客[2—10];②从公交运行者或者公交系统的角度出发,为降低其运营成本或使其运营收人(效益)最大,希望公交单趟运行时间最小[11—15]。Chien[13,15]等人考虑公交车辆的载运能力后,提出公交发车间隔和站距之间的关系模型。Ibeas[16]等人研究由于停靠站地理位置、公交运行、交通拥堵及地区人口属性不同而引起的交通需求变化,建立了最优站距的双层优化数学模型,并将这一模型运用于实例中。

目前,在公交站距方面的研究存在着不足:①很少考虑公交站距对乘客的影响;②没有一种合适的转化函数能映射出中国当前的时间价值;③以往研究的模型及其参数取值均与中国的实际情况存在着较大的差异。

作者拟从乘客出行时间、公交服务率及公交系统运行角度出发,分别分析站距对其的影响,评价现今中国交通体系中不同公交站距的优劣所在,建立多目标规划站距模型,用不同算法求解模型和进行敏感度分析,以提取适合中国国情的公交最优站距。

1 模型建立

建立多目标优化模型包括4个步骤:①计算乘客平均公交出行时间;②计算公交运行消耗时间;③计算公交服务的覆盖面积;④建立多目标优化模型。

1.1 中国居民的公交出行特征分析

在最优站距的研究中,考虑到居民的出行特征和公交系统的运行要求,从模型的假定到建立,与以往的研究有2点不同:

1)以往的公交站距研究将居民的出行距离简化为某一固定值。但实际中,居民的出行距离往往和城人口结构与城市规模有很大的关系。例如:小城市居民的出行距离往往小于大、中型城市的,老龄化人口很多的城市居民出行距离往往小于新兴城市的。在本研究中,采用出行距离函数来反映中国居民出行的距离分布。

2)以往的公交站距研究假定是公交车在停靠站可以跳站。但实际中,公交系统的运营者(公司)明确规定了公交车必须逢站必停、不允许跳站。在本研究中,公交的停靠为逢站必停。

经过对中国20个大、中城市的居民出行调查,得知居民出行距离的分布近似符合皮尔逊Ⅲ型分布,即Γ分布,其概率密度函数为:

假设乘客步行到达(离开)公交线路出行,沿公交线路出行的距离分布也符合Γ分布,在模拟居民采用公交出行方式的出行距离过程中,取r= 2[10],则

对于研究的不同点2),在进行乘客出行时间和公交运行时间计算时,遇到公交停靠站,就会考虑公交车辆在站点的停靠行为。根据公交乘客的分布累加公交的停靠时间,反映公交不允许跳站的特征。

1.2 公交站距对乘客出行时间的影响

设i为乘车车站区间,1≤i＜int(L/D),则出行距离介于i D—X～i D+Y的概率为:

乘客乘坐公交全程的概率为:

乘客步行到达公交线路的距离为:

进而,乘客平均公交出行时间为:

式中:Tp为乘客车外总出行时间;Tb为乘客车上总出行时间;T1为乘客从出行起点(O点)到达公交车站的时间;T2为乘客在公交车站候车的时间;T3为乘客从公交车站到达出行终点(D点)的时间;T4为乘客车内匀速运行时间;T5为停车上(下)客时间。

乘客由起点步行到达公交站点的时间与周围道路网密度、公交线路网密度及设站的距离密切相关。将乘客步行到站过程分解为从起点步行到达公交线路和沿公交线路步行到达公交车站2个部分。乘客步行到达公交线路的时间为:

式中:T11为乘客从起点步行到达公交线路的时间;vw为乘客步行速度。

对于乘客沿公交线路步行到达公交车站的时间,则要分析乘客与相邻2个公交车站的距离和分界距离的关系,如图1所示。

图1 乘客沿公交线路步行示意Fig.1 Illustration of walking critical distance

假设乘客在选择公交车站时按出行时间最小选取车站,则上车前乘客沿公交线路到车站的时间为:

式中:TR为公交车匀速运行1站的时间。

对式(8)取两边相等,得相邻2车站的选择分界线:

进而得到乘客选择站点的临界距离:

则乘客沿平行公交线路方向的步行平均距离为:

乘客沿公交线路方向的步行时间为:

则乘客从O点到公交车站的时间和乘客从公交车站到达出行终点的时间分别为:

乘客的候车时间与乘客的到达分布和公交车的发车频率等因素密切相关。因此,在乘客随机到达车站的情况下,假定其平均候车时间为发车间隔的一半,即乘客平均候车时间为:

式中:h为平均发车时间间隔。

乘客公交车内运行时间是公交车在公交车站间以匀速行驶所消耗的时间,这与公交车的运行车速有关。根据乘客出行距离概率,得乘客平均车内运行消耗时间为:

式中:vb为公交车辆的平均速度;Pi为乘客选择站点i的概率。

公交车减速进站、候车及加速离站的运行过程如图2所示。对于加速离站和减速进站的过程,为方便分析,假设为匀加(减)速运动。因此,公交车减速进站、候车及加速离站所消耗的时间为:

式中:a为公交车到站的加速度;b为公交车离站的减速度;tas为车辆平均上、下客时间。

将出行各个部分的时间代人出行总耗时公式,得乘客乘公交车出行所消耗的平均时间:

图2 公交车运行示意Fig.2 Illustration of bus running

1.3 公交站距对公交出行时间的影响

公交出行时间可表示为:

式中:Ta,d为公交加速(减速)所消耗的时间;Ts为公交站点停靠延误所消耗的时间;Tc为由于信号控制引起公交所消耗的时间;To为公交在正常行驶所消耗的时间;Tm为其他没有列举的延误所消耗的时间。

在中国,规定公交车必须在其线路上的每一个停靠站停靠,因此,公交加速(减速)所消耗的时间为:

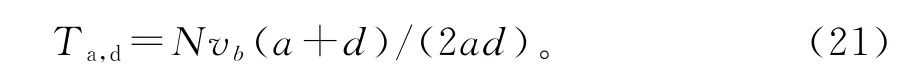
式中:N为公交停靠站数量;a为公交加速度;d为公交减速度。

公交站点停靠造成的延误为:

式中:qs为期望小时公交客流;t为每位乘客的上(下)车平均服务时间;k为平均开、关门时间。

公交正常行驶所消耗的时间为:

式中:L为单程公交行驶距离。

在进行最优站距的研究时,由于已知公交线路的长度和走向,无论站距如何变化,都不会对交通管控延误以及其他延误产生影响,因此,可假设两者为定值,则

因此,最终的公交出行时间为:

1.4 公交站距对公交服务面积的影响

作为社会福利与解决城市交通拥堵问题的重要手段,在进行站距优化设计时,不仅要从乘客的角度出发考虑单个乘客的出行时间最小,从公交运行公司的角度出发考虑公交车运行时间最小,还应从社会的角度出发考虑公交服务覆盖尽可能大的城市面积。由于公交服务是通过停靠站的上(下)客和乘客换乘实现的,对单个停靠站来说,其服务覆盖半径一定,因此,站距的大小将影响整条公交线路的服务面积。公交的服务面积为:

单位长度公交服务覆盖面积为:

1.5 多目标优化模型

在确定了公交线路的长度和走向后,不同的站距取值将会影响乘客的出行时间、公交的运行时间及公交服务的覆盖面积。基于此,建立多目标规划模型:

2 求解算法

求解多目标规划模型之前,必须标定一些相关的参数。经过调查,获得了南京市居民的步行极限可接受距离为465 m,平均公交出行距离为5.6 km。

对于多目标规划模型,本研究采用了2种解决方法:①转化法,即通过转化,将多目标规划转变为单目标规划,之后采用遗传算法判敛并求解;②直接求解法,即直接对现有多目标规划问题求解。在现有向量评估遗传算法(Vector Evaluated Genetic Algorithms,简称为VEGA)的基础上进行修正,通过修正后的MVEGA算法求解,给出问题的最优解。在居民出行距离分布函数中,参数λ的标定采用牛顿二分搜索法确定。

求解方法 ①的思路是对多目标规划的目标进行转化,将涉及到的3个目标通过乘除法转化为单目标。对转化得到的单目标利用遗传算法判敛并输出站距。

求解方法②的思路是不改变多目标规划问题,在现有向量评估遗传算法的基础上进行修正。对修正后的MVEGA算法进行求解,得到问题的最优解。该求解流程如图3所示,求解方法包含6个步骤:

图3 求解流程Fig.3 Flowchart of direct solution method

1)计算不同站距D时的Tbus,T和P。

2)初始化种群,设i=0,种群大小M=60。定义目标函数f1为min Tbus,f2为min T,f3为max P。

3)结束判断。当i=N时,得到了最优的站距D,算法停止;否则,进人4)。

4)i=i+1。将种群均分为3个子种群,对应目标函数f1,f2和f3。各个子种群的大小为20,对应目标函数分别计算其适应度。

5)个体选择。采用轮盘赌的方式,分别从各个子种群中选择个体。

6)交叉、变异。将3个新的子种群合并,选择合适的交叉、变异概率,得到新的种群。

这些求解方法均采用Microsoft Visual C++6.0实现,其结果和案例见敏感性分析。

3 敏感性分析

敏感性分析可以用于挖掘影响公交站距各种参数之间的相关关系。每个参数的变化均是基于参数的基础数值及其计算得到的最优值而开展的。部分参数由南京市2路和11路公交的调查得:a=1.0 m/s2,d=—1.2 m/s2,vb=8 m/s和vp=1.2 m/s。

在敏感性分析中,采用OD矩阵反映公交系统运行的需求和公交线路的发车间隔。为了更方便地进行敏感性分析计算,引人一个新的变量Tad来代表平均停靠时间。假定每个站点的平均停靠时间均为定值,则其值可由Tad=qsτ+k计算得到。

公交线路长度为15 km,步行极限距离R= 400 m时,不同平均出行距离和平均停靠时间下的最优站距见表1。从表1中可以看出,当乘客平均出行距离较小时,2种求解方法的结果接近。当乘客平均出行距离较大时,转化法的求解结果比直接求解法的保守,其值变化不明显(Lc=5 km与Lc=6 km时转化法的结果相同),因为采用转化法时,将3目标转化为单目标后,单目标对乘客出行时间的小变化并不敏感,会出现对乘客出行时间最小这一目标不敏感的现象。因此,除求解方便外,为更好地反映最优站距与3个规划目标间的关系,用直接求解法分析。

表1 最优站距(R=400 m)Table 1 Optimum spacing of different solution algorithms(R=400 m)

公交线路长度为15 km、步行极限距离R= 500 m时,用直接求解法得到的不同平均出行距离和平均停靠时间下的最优站距见表2。从表2中可以看出:当居民平均出行距离一定时,最优站距随平均停靠时间的增加而增加;同样,在平均停靠时间一定时,最优站距随居民平均出行距离的增加呈增加的趋势。

不同步行极限距离下的最优站距如图4所示。从图4中可以看出,随着步行极限距离的增加,最优站距也随之增加,两者呈线性相关。因此,采用回归分析,得到两者之间的线性回归函数及相关性。

表2 最优站距(R=500 m)Table 2 Optimum spacing of different solution algorithms(R=500 m)

图4 最优站距和步行极限距离的关系Fig.4 Optimum spacing and limited walking distance for various bus line lengths

式(30)～(33)分别为公交路线长度为12, 14,16和18 km时的回归函数。该结果证明了最优站距和居民步行极限距离之间的关系。

不同居民平均公交出行距离下的最优站距如图5所示。同理,两者呈线性相关,回归分析的结果为:

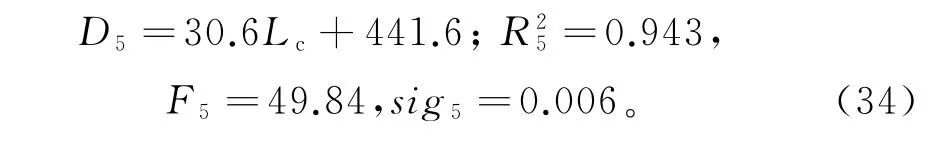
图5 最优站距和平均出行距离的关系Fig.5 Optimum spacing vs.average travel distances for various limited walking distances

最优站距与平均停靠时间的关系如图6所示。在线路长度一定的前提下,最优站距随停靠时间的增加呈增加的趋势。

图6 最优站距和平均停靠时间的关系Fig.6 Optimum spacing and average stop interval for various limited walking distances

以南京市11路公交车为例,说明本研究提出方法的可行性。11路公交车开始于鼓楼区龙江新城市广场,终点站位于栖霞区月苑小区,总长为14.3 km。11路是南京最为繁忙的一条公交线路,共有站点23个,现状站距为650 m。11路的运行参数为:L=14.3 km,a=1.0 m/s2,d=—1.2 m/s2,vb=8 m/s,vp=1.2 m/s,h=300 s,Tad=14 s,R=465 m,Lc=5.6 km。

根据运行参数,建立了南京市11路公交最优站距的多目标优化模型。采用直接求解法求解,得到了站距的优化值为690 m,略大于现有值。

4 结论

MVEGA法要优于模型转化法。基于敏感性分析发现,公交车最优站距对平均出行距离和最大步行距离更加敏感。通过南京市11路公交的实测数据,验证了作者提出的最优站距确定方法的准确性。选择用出行距离分布函数来表征出行距离的变化,研究站距对乘客出行和公交系统运行时间的影响,并将公交服务的覆盖引人模型。本研究提出的最优公交站距模型可以较好地模拟中国出行特性下公交站距的设置,并确定符合多种出行需求最优站距的取值。

本研究存在部分缺陷。在后续的研究中,①应该考虑更多的接驳方式的模型假设,如:采用私家车和地铁等交通方式与公交接驳等;②因为接驳方式的多样性,后续研究对公交服务半径的定义将被大大扩充,由此而引起的公交服务覆盖半径的确定方法有待研究。③现有研究方法是在遗传算法基础上修正的,其准确性有所提高,但在后续研究中希望能找到一种更简单、快速与准确的求解方法。

[1] Lwsley.Optimum bus spacing:Part 1[J].Traffic Engineering and Control,1976,17(11):399—401.

[2] Vuchic V R,Newell G F.Rapid transit interstation spacings for minimum travel time[J].Transportation Science,1968,2(2):303—309.

[3] 戴炳奎.快速公交站点布局设计优化研究[D].成都:西南交通大学,2012.(DAI Bing-kui.Optimization and planning of stop spacing for bus rapid transit [D].Chengdu:Southwest Jiaotong University,2012. (in Chinese))

[4] 陶永俊.中心城区道路交叉口公交站点设置优化研究[D].湘潭:湖南科技大学,2013.(TAO Yong-jun.Optimization of bus stops at intersections of downtown areas[D].Xiangtan:Hunan Science and Technology University,2013.(in Chinese))

[5] 葛宏伟.城市公交停靠站点家头影响分析及其优化技术研究[D].南京:东南大学,2006.(GE Hong-wei.A-nalysis and optimization technology of the influence of bus stops on traffic[D].Nanjing:Southeast University,2006.(in Chinese))

[6] 覃商.轨道交通枢纽规划与设计理论研究[D].上海:同济大学,2002.(QIN Yu.Rail transit planning and design theory[D].Shanghai:Tongji University,2002. (in Chinese))

[7] Gleason J M.Set covering approach to the location of express bus stops[J].Omega,1973,3:605—608.

[8] 胡刚.城市公共交通网络及站点优化技术研究[D].南京:东南大学,2003.(HU Gang.Research for optimization practical technology of urban public transit network and stop[D].Nanjing:Southeast University, 2003.(in Chinese))

[9] 周葵,黄奕皓,罗小东.基于公交系统费用最小的公交站距优化模型[J].公路与汽运,2014(4):44—47. (ZHOU Kui,HUANG Yi-hao,LUO Xiao-dong.Bus stop spacing optimization model based on minimized cost of transit system[J].Highway and Automotive Applications,2014(4):44—47.(in Chinese))

[10] 杨晓光,徐竞琪,刘好德,等.基于乘客平均出行时间最小的公交站距优化模型[J].吉林大学学报:工学版,2008,38(4):802—807.(YANG Xiao-guang,XU Jing-qi,LIU Hao-de,et al.Stop spacing optimization model based on minimizing average travel time of passengers[J].Journal of Jilin University:Engineering and Technology Edition,2008,38(4):802—807. (in Chinese))

[11] Anthony A S.Model for determing optimum busstop spacing in urban areas[J].Journal of Transportation Engineering,2001,127(3):195—199.

[12] 李英帅,姚红云,秦雷.基于站点取消与合并原理的公交站距优化方法[J].重庆交通大学学报:自然科学版,2011,30(6):1370—1374.(LI Yin-shuai,YAO Hong-yun,QIN Lei.Bus station optimization method based on the principle of station canceling and station combining[J].Journal of Chongqing Jiaotong University:Natural Science Edition,2011,30(6): 1370—1374.(in Chinese))

[13] Chien S,Yang Z.Optimal feeder bus routes with irregular street networks[J].Journal of Advanced Transportation,2000,34(2):213—248.

[14] Chien SI,Qin Z,Liu R.Optimization of the bus stop location for improving transit accessibility[J]. Transportation Planning and Technology,2004, 27(3):211—227.

[15] Chien S,Yang Z,Hou E.A genetic algorithm approach for transit route planning and design[J]. Journal of Transportation Engineering,2001,127(3): 200—207.

[16] Ibeas A,Dell’Olio L,Alonso B,et al.Optimizing bus stop spacing in urban areas[J].Transportation Research:Part E,2010,46:446—458.

A multi-objective optimization model to determine the bus stop spacing in urban areas of China

LIU Xin-rong,SU Wei-cheng
(Nanjing Urban Construction Management Co.,Ltd.,Nanjing 210000,China)

In order to better understand the optimum stop spacing in China and the influence of different stop spacing on passenger and bus travel time as well as transit system, a multi-objective optimization model is developed to estimate the relationship between stop spacing and average passenger travel time,one-way total bus travel time and bus service area,respectively.Then the modified vector evaluated genetic algorithm method (MVEGA)as well as a transformation method with genetic algorithm is introduced to solve the model.The results show that MVEGA method is better than the transformation method.A sensitivity analysis is demonstrated that the optimum spacing is more sensitive to the average travel distance and the limited walking distance,and an example of No.11 bus in Nanjing is used to verify the model with the optimum stop spacing of 690 m.Compared with previous studies.A travel distance distribution function to calibrate the probability of different travel distance is introduced.The impacts of stop spacing on the passenger and bus travel time correspondingly are estimated.The bus service areas are taken into account.

stop spacing;multi-objective optimization;travel distance;travel time;genetic algorithm

U491.1+7

A

1674—599X(2015)04—0081—07

2015—05—18

江苏省研究生创新基金项目(CXZZ12_0116);东南大学优秀博士学位论文基金项目(YBJJ1345)

刘听嵘(1987—),男,南京城建项目建设管理有限公司助理工程师。