路段容量约束下路网结构与OD分布的最优匹配
2015-11-26张晓艳王丽娇
张晓艳,王丽娇
(长沙理工大学 交通运输工程学院,湖南 长沙 410004)
路段容量约束下路网结构与OD分布的最优匹配
张晓艳,王丽娇
(长沙理工大学 交通运输工程学院,湖南 长沙 410004)
基于路段容量约束,寻找与路网布局相匹配的OD分布,探索解决交通供需矛盾的途径。将城市路网分为若干交通小区,假设每一交通小区之间的OD为未知量,并且定义了合适路径这一新的概念。利用合适路径理论,找出若干条满足条件的各个小区之间的出行路径,建立线性规划模型,并求解出每条路径流量以及各个交通小区的OD量与路网布局匹配的OD分布,得到路网的最大容量,分析了路网容量与合适路径待定系数之间的变化关系。对交通规划路网流量分析、交通小区开发强度控制和交通组织具有一定的参考价值。
路段容量约束;路网布局;路网容量;OD分布
交通是城市经济社会的命脉。通畅、便捷的城市交通对实现城市的功能和促进社会经济的发展起着至关重要的作用[1]。随着城镇化进程的加快,城市人口的不断增长,出行机动化水平越来越高,随之而来的交通拥堵问题也越来越严重[2]。由于早期城市规划和交通规划知识的缺乏,造成城市规划和交通规划的盲目性[3]。这种盲目性存在着很多弊端(例如:造成客、货源的集散点与路网结构的不匹配,即OD分布与路网结构不匹配,导致交通供给与交通需求的不均衡),是造成交通拥堵的根本原因。现在,交通拥堵已经成为最困扰城市发展的城市病之一。要想解决交通问题,不能靠限号出行、多修路及限购新车等治标不治本的措施。因此,必须从交通规划开始,让每一个城市拥有一个健康可持续发展的交通网络,从根源上解决交通供需的矛盾。与路网布局匹配的OD分布对现有路网的交通规划和城市规划都具有很好的指导作用,对路网改造和交通小区的开发强度控制也具有现实指导意义,同时,使交通拥堵在一定程度上得到缓解。
1 基本原理
交通网络是典型的复杂网络,而且是由道路网络和出行网络组成的双层复杂网络,因此交通网络的容量(简称为路网容量)不仅得考虑道路条件,还得考虑出行网络的布局,考虑两者之间的互相影响[4]。
路网容量是指在一定的道路和交通条件下,交通个体遵循出行费用最少的原则,单位时间内所能处理的最大OD流量之和。路网容量反映城市道路网总体建设水平,是交通供给能力的宏观体现。它既是衡量道路交通供需平衡、决定投资方向的决策指标,也是城市总体规划以及城市道路规划中的一项基础资料和重要决策指标[5—6]。基于路段容量约束,以路网容量的大小为标准,判断路网结构与OD分布是否匹配。即当路网容量最大时,OD分布为与路网结构最匹配的OD分布形态。很显然,当交通小区出行距离越短时,路网容量越大。这时车辆占用的道路资源最少。可见,道路服务的车辆总数越大,即路网容量越大。但实际情况并非如此。人们的出行并非只是在距离最短的区间内进行,它由人们的生产活动决定。人们的出行网络是一种复杂的出行网络。因此研究与路网结构匹配的OD分布具有现实意义。
2 模型的建立
设:xa为路段a上的交通流量;frsk为出发地(r)与目的地(s)OD之间第k条路径上的交通流量;δrsa为0~1变量(如果路段a在出发地(r)与目的地(s)OD之间的第k条路径上,则δrsa=1;否则,δrsa,k=0);Z为路网容量;Ca为路段a上的通行能力;N为网络中节点的集合;L为网络中路段的集合;R为网络中出发地的集合;S为网络中目的地的集合;ψrs为r与s之间所有路线的集合。
模型的约束条件:路网容量应等于OD交通量即OD间各条路径上的交通总量。其公式为:

模型的非负约束条件为:

路径交通量frsk与路段交通量xa之间的关系式为:

实际生活中,人们出行不全会选择最短路径,会根据自己获得的信息选择一条比较合理适合自己的路径。例如:人们通常会选择路程比较短、费用比较少的路段。除了最短路以外,这样满足条件的路径还存在若干条,它们的一个共同点是:路程与最短路在一定范围内相比较,不会无上限地增加。人们选择合适路径的制约因素是路程、费用及时间[7]。在3个因素中,路程是决定费用和时间的最重要因素。本研究仅考虑路程对路径的影响,选择用路程来控制合适路径。合适路径的约束条件为:

式中:n为待定系数;s最短路为出行距离最短的路径。
由于人们选择的路径不会小于最短路的长度,也不会无限制的增加。因此n为一个大于1的数,该系数的取值与人的行为有关。例如:当一个城市的交通拥堵比较严重,人们可以接受绕远到达目的地时,取值就比较大;当一个城市交通不拥堵,人们去哪里都可以选择最短路时,取值就比较小。人们很难接受超过3倍最短路距离的路径,因此本研究的待定系数小于3。
因为普通路段都是双向通车的,并且每个方向的车道数与通行能力一致,且与其他道路条件也一致,所以用这种算法求解出的OD分布一定是对称的,可以只计算一个方向的OD分布。例如: A—B的OD流量与B—A的OD流量是一样的。
3 模型的计算
在路网条件已知的情况下,即路段的通行能力已知,在不考虑节点通行能力的基础上,求解与路网结构匹配的OD分布[8—11]。
1)根据约束条件,选择合适路径。
2)基于最大流理论,以路网容量最大为目标函数,建立线性规划模型。
目标函数:

约束条件:
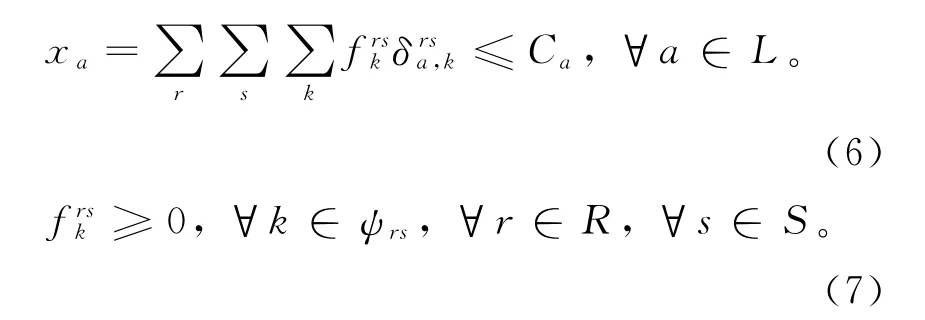
3)运用Matlab软件,根据单纯形法求解此线性规划,即得到在路网结构已知的情况下每条合适路径上的流量,此时的路网容量达到最大。
4)得到路径流量后,求出OD分布矩阵。在此OD分布下,将求得的路径流量代人式(3)中。如果路径流量之和小于路段通行能力,则说明该道路资源没有被充分利用,可设法引导车辆在该道路上行驶,以减轻其他道路的交通压力;如果路径流量之和等于路段通行能力,则说明该路段为瓶颈路段[12]。要想提高路网通行能力,则需要扩容;或者引导车辆走其他不拥堵的路段。
4 算例
已知路网如图1所示,有A,B,C和D 4个交通小区,11条路段,路段的长度和通行能力见表1,求解与此路网结构匹配的交通小区的OD分布。

图1 路网布局结构Fig.1 The layoutstructure of the road network

表1 路段长度数据Table 1 Data of the link length
1)取合适路径的待定系数为1.5,则合适路径的约束条件为:合适路径≤1.5×最短路径长度。
求解出此路网的合适路径为:A—B:2,1—4; A—C:3,1—6;A—D:1—5—9,2—7—11,3—10, 1—4—7—11,1—6—10,2—4—5—9;B—C:4—6; B—D:7—11;C—D:10,8—9。
2)OD对间的流量分别为OA—B,OA—C,OA—D,OB—C,OB—D和OC—D;每条路径上的流量分别为和;路段上的流量分别为x1,x2, x3,x4,x5,x6,x7,x8,x9,x10和x11;路段上的通行能力分别为C1,C2,C3,C4,C5,C6,C7,C8,C9, C10和C11。
以路网容量最大为基本原则,求出最优的路径流量。
目标函数为:

约束条件为:
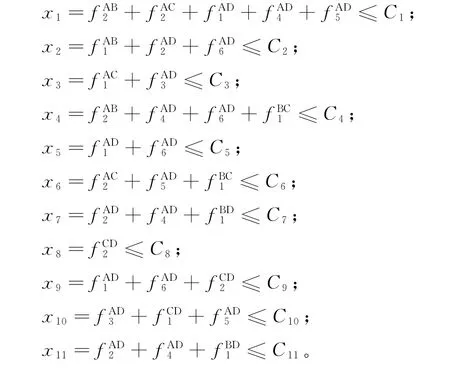
3)这是一个线性规划问题,利用单纯形法原理,运用Matlab软件求解。
求解出的结果为:

最大路网容量max(Z)=10 000。
当合适路径的待定系数为1.3时,最大路网容量为9 000;当合适路径的待定系数为1.8时,最大路网容量为10 400;当合适路径的待定系数为2.1时,最大路网容量为10 400。
4)从计算结果中可以看出,假设的合适路径不一定会有车走;路程越短的路径上分配的流量越多,这样才可以节约道路资源,使路网容量达到最大。而且随着合适路径数量的不同,路网的最大容量也会变化,但是总有一个极限。
5 结论
通过本研究建立的模型,求解与路网结构匹配的OD分布,能够有效解决交通供需矛盾,对交通规划与城市规划具有重要的现实意义。在城市规划时,在现有路网的基础上,计算出匹配最优的OD分布。与实际OD分布对比,对于未饱和的交通小区,增加其开发强度;对于已经饱和的交通小区,则抑制其开发强度。当路网结构发生变化(如:某条道路处于维修阶段)时,路网通行能力受到的影响可以通过该模型计算出来;也可以发现路网当中比较重要的路段或者制约路网容量增加的瓶颈路段;同时也可用该模型做出一些交通诱导措施,使很多车辆避免通过同一交通瓶颈路段。
[1] 李炳林.基于路网服务水平的路网容量研究[D].长沙:长沙理工大学,2008.(LI Bing-lin.Research on the capacity of the road network based on the level of the network service[D].Changsha:Changsha University of Science&Technology,2008.(in Chinese))
[2] 张晓婷,吴兵.考虑特定OD分布形态的路网容量双层规划模型[J].交通运输工程与信息学报,2012(4): 116—123.(ZHANG Xiao-ting,WU Bing.Level programming model for the road network capacity based on the existed OD distribution[J].Journal of Transportation Engineering and Information Technology, 2012(4):116—123.(in Chinese))
[3] 杨晓萍,杨国志.基于网络最大流的城市道路网容量计算[J].上海公路,2012(2):53—56.(YANG Xiaoping,YANG Guo-zhi.Based on the network maximum flow of the urban road network capacity calculation[J].Shanghai Road,2012(2):53—56.(in Chinese))
[4] 邢晓欢,程琳.路网布局结构对路网容量的影响研究[J].交通运输工程与信息学报,2008(3):109—114. (XING Xiao-huan,CHENG Lin.Research of road network layout structure influence on the road network capacity[J].Journal of Transportation Engineering and Information Technology,2008(3):109—114.(in Chinese))
[5] 李波,陈金山.基于OD反推的路网承载能力分析及应用[J].西华大学学报:自然科学版,2012(2):38—41.(LI Bo,CHEN Jin-Shan.The network bearing capacity analysis and application based on OD estimation[J].Journal of Xihua University:Natural Science Edition,2012(2):38—41.(in Chinese))
[6] 郑志鹏,卢守峰,王杰.一种基于开源软件的OD反推求解算法[J].交通科学与工程,2015,31(1):98—102.(ZHENG Zhi-peng,LU Shou-feng,WANG Jie. An OD estimation algorithm based on the opensource package[J].Journal of Transport Scienc and Engineering,2015,31(1):98—102.(in Chinese))[7] 陈新.城市交通网络布局与优化策略研究[D].武汉:华中科技大学,2005.(CHEN Xin.The strategy of the optimization and planning for the urban traffic network[D].Wuhan:Huazhong University of Science and Technology,2005.(in Chinese))
[8] 杨晓萍,杨国志,赵方,等.多起终点交通流的城市道路网容量计算[J].华东公路,2005(4):18—20. (YANG Xiao-ping,YANG Guo-zhi,ZHAO Fang,et al.Multiply end of the traffic flow of the urban road network capacity calculation[J].East Iva Highway, 2005(4):18—20.(in Chinese))
[9] 崔晧莹,寇玮华,丁振.多品种流交通网络的最大流算法研究[J].交通运输工程与信息学报,2014(2):77—82.(CUI Hao-ying,KOU Wei-hua,DING Zhen.Study of the maximum flow algorithm for the multicommodity flow traffic network[J].Journal of Transportation Engineering and Information Technology,2014(2):77—82.(in Chinese))
[10] 谢辉,于晓桦,晏克非.城市道路交通网络系统容量评估模型[J].中国公路学报,2012(3):129—134, 146.(XIE Hui,YU Xiao-hua,YAN Ke-fei.Evaluation model of urban road network system capacity [J].China Journal of Highway and Transport, 2012(3):129—134,146.(in Chinese))
[11] 苏镇洪,赵文秀,龙科军.道路网络容量的多端最大流算法[J].交通科学与工程,2012,28(1):84—88. (SU Zhen-hong,ZHAO Wen-xiu,LONG Ke-jun.A-nalysis of the road network capacity based on multiterminal network maximum flow algorithm[J]. Journal of Transport Scienc and Engineering,2012, 28(1):84—88.(in Chinese))
[12] 朱森来,程琳,许项东.基于储备容量的交通网络潜在瓶颈路段识别[J].系统工程理论与实践,2014(6): 1572—1577.(ZHU Sen-lai,CHENG Lin,XU Xiang-dong.Identifying bottleneck links in transportation networks based on the reserve capacity[J]. Systems Engineering-theory&Practice,2014(6): 1572—1577.(in Chinese))
The optimal matching based on the link capacity constraints to find network structure and OD distribution
ZHANG Xiao-yan,WANG Li-jiao
(School of Traffic and Transportation Engineering,Changsha University of Science&Technology,Changsha 410004,China)
Based on the link capacity constraints,the OD distribution which is matched with the road network layout and explore how to solve the contradiction between traffic supply and demand is found.The urban road network are divided into some traffic areas, and the OD between each traffic area is assumed as the unknown number,at the same time that the new concept of the right path is defined.The theory of the right path is applied to find out the article number of paths between the areas and also meet the conditions,while the linear programming model is established.Each way runoff and the OD of each traffic area are solved.The OD distribution which is matched with the road network layout is obtained.The maximum capacity of the road network is calculated.The variable relationship between the road network capacity and the undetermined coefficient of the appropriate path are analyzed.This research will play a role in the analysis of road network traffic,traffic planning,road network traffic analysis,the control of traffic area development-intensity and organization in traffic.
link capacity constraints;road network layout;road network capacity;OD distribution
U491.1+2
A
1674—599X(2015)04—0077—04
2015—06—03
国家自然科学基金项目(51338002)
张晓艳(1989—),女,长沙理工大学硕士生。
