氨基酸疏水性对蛋白质结构的影响
2015-11-26史小红
史小红 范 倩
氨基酸疏水性对蛋白质结构的影响
史小红 范 倩
本文应用计算机模拟方法对蛋白质折叠结构进行分析,研究了在二维的HP模型下,采用Monte-Carlo算法,运用F-P法、K-D法、沃氏法、埃氏法及米氏法,几种常见的对氨基酸残基疏水特性的不同划分方法,从序列的正反两个方向对真实蛋白质折叠结构进行计算机模拟研究。研究结果表明,同一种疏水特性值从序列的正向或是其反方向开始折叠,蛋白质折叠的最小能量构象的能量值相等;各疏水特征参考值求得的最小能量构象及能量值存在差异。
从蛋白质的序列出发研究蛋白质的折叠结构,是现代生物信息学研究的一个重要的目标。生物体的遗传信息是由DNA转录为RNA后,再有RNA翻译而成为各种具有稳定功能的蛋白质,以完成各种生命活动。所以,研究蛋白质折叠结构有助于我们了解蛋白质空间结构与其功能的关系,帮助我们破译遗传信息这一生命之谜。蛋白质的折叠结构决定蛋白质的功能,错误的折叠会形成无活性的蛋白,从而引起阿尔茨默、帕金森、亨廷顿等蛋白质的折叠疾病。研究蛋白质的折叠结构机理,可以帮助我们在蛋白质工程、药物设计和筛选、基因疾病的治疗等方面,对天然蛋白质结构进行有目的的改变,从而改变蛋白质的功能,达到对基因疾病的控制。
据美国的蛋白质结构数据库有关数据的统计,到目前为止,约有十万种蛋白质分子被发现,但已测定结构的蛋白质数量仅约一万种,约占总量的10%。实验在研究蛋白质折叠时,现常用的方法一般为X射线衍射法和多维核磁共振法,但由于蛋白质分离提纯化技术要求非常高,蛋白质晶体难以培养,晶体结构测定周期长等因素,从而制约了蛋白质研究的进展。所以利用计算机技术模拟蛋白质结构折叠,采用理论预测的方法来研究蛋白质的结构,可以帮助我们解决序列与结构在数据上差别越来越大的问题。
研究蛋白质的折叠,需要明白蛋白质折叠的机理。假如一个蛋白质为仅含有100个氨基酸残基,为简化计算,若每个氨基酸的残基在折叠结构的二维空间位置用两个几何参数来表示,那么必须引入200个特定的几何参数才能把折叠的蛋白质完整的表达出来,假定每个参数只取两个数值,则这个100个氨基酸残基组成的小蛋白质,折叠出现的可能构象就有2200=1.6×1060,假如从蛋白质的一个折叠结构到另一个折叠结构需要10~13s,那么确定一个合适的折叠结构,总的探索时间将需要1.6×1060×10~13s,大约为5×1039年。但实际的蛋白质折叠时间一般仅需几分钟甚至几秒钟就能完成。这一现象表明,蛋白质的折叠是一个高度定向且多因素控制的过程。
蛋白质的折叠是一个非常复杂的过程,受到组成蛋白质的20种氨基酸残基的影响。影响蛋白质结构的维持和稳定的因素一般有静电作用、氢键、范德华力、残基的亲水性和疏水性、配位键、二硫键等其他因素。在建模时必须尽可能的简化模型,所以只考虑对蛋白质折叠结构影响最大的因素研究。现在越来越多的人已经认识到,氨基酸残基的亲疏水作用力是维持和稳定蛋白质构象的主要作用力,即在求最小能量函数时,仅考虑疏水作用力。
本文基于20种氨基酸残基的疏水性特征值的几种不同划分法,采用二维的HP模型,搜索方法采用Monte-Carlo法,模拟真实蛋白质的一级氨基酸残基序列从正反两个方向来搜索蛋白质折叠的最小能量构象。
研究方法
1.数据集
本文从真实蛋白质1AEP中,截取其中13个一级氨基酸残基序列,其序列为为LEU THR ASN VAL GLY HIS GLN TRP GLN ASP ILE ALA THR。真实蛋白质1AEP的数据从美国的蛋白质结构数据库(RCSBProtein Data Bank,简称RCSB PBD)中下载。网址http://www.rcsb.org。
文中对20种氨基酸残基疏水特性的参数参见表1。
表1是根据文献4的表4改编而成。其中K-D法和埃氏法是同时考虑了氨基酸在有机溶剂和水中的分配系数,以及氨基酸在蛋白质结构中的分布情况而确定的;米氏法只考虑了氨基酸在蛋白质结构中的分布;F-P法的实验基础是氨基酸在辛醇和水中的分配系数;沃氏法则是测量了氨基酸从水到蒸汽时的自由能△G后,推算所得。在表1中,负值越大,疏水性越弱,亲水性越强。括号中的数字是按这种方法得出的疏水性由强到弱的序列。在沃氏测量法中,未确定脯氨酸的亲疏水特性参数,我们根据前四种分类方法,在进行HP转化时将其视为亲水性氨基酸残基。
模型与算法
模型
考虑影响蛋白质结构的维持和稳定的主要因素,即在计算最小能量函数时只考虑疏水性作用力的影响。1989年,Dill提出了疏水性-亲水性(HP)模型,本文将蛋白质序列视为一列由疏水性氨基酸(用方格表示,记为H)和亲水性氨基酸(用圆圈表示,记为P)组成的链,即将原有的链转化为了一条只含有H和P组成的序列。将二维空间作等距离划分,连接网格线,HP链上的每个节点可向前、后、上、下四个方向90°旋转。即在二维折叠空间中,有四个折叠方向,分别用两位二进制数表示,00表示向右,11表示向左,01表示向上,10表示向下。如图1所示。
定义能量函数为:每一对非直接相连但相邻的疏水性残基(记为H:H)间相互作用的能量为-1,其他为0。用此能量函数,寻找到最小能量的构象为一个疏水核聚集在结构内部的紧凑构象。能量函数记为Eh。即

其中,δi表示肽链上第i个氨基酸残基,可取H或P,γi表示第i个小球,若γi-γj表示H没有直接相连但相邻,则Φ(γi-γj),否则为0。
运用此模型求得的最小能量构象以及最小能量值均与前人所求得的结果相符。如图2所示,为一条由13个氨基酸序列HHPHPHPHPPHPH的最小能量的可能构象,其最小能量值为-6。这种结构符合人们对蛋白质构象的认识:疏水性氨基酸残基一般深藏于蛋白质分子的内部,而亲水性氨基酸残基则暴露在蛋白质表面,以便于与水接触。
算法
从计算的角度来讲,蛋白质结构折叠的构象搜索的问题为典型的NP难题。解决这一问题现常用的算法有遗传算法、模拟退火法、蚁群算法及Monte-Carlo算法等。本文所用的搜索算法为Monte-Carlo算法。Monte-Carlo算法,简称MC法,为一种随机搜索算法。它是根据所求解问题的变化规律,先构造一个合适的概率模型,再根据模型进行大量的统计试验,它的某些统计参考量,正好是待求解问题的解。它的优点在于收敛速度与问题的维数无关,且误差容易确定。
本文用于搜索蛋白质折叠的最小能量可能构象的MC方法可描述如下:
第一步 从一个随机的构象S1出发,随机产生一个种群数为200的初始种群数,计算能量值Eh;
第二步 找出初始种群数中能量最小的构象Si,并计算最小能量值Ehi;
第三步 对Si的某个残基定向进行随机改变,形成新构象Sj,并计算其能量值Ehj;
第四步 如果Ehi>Ehj,接受构象Sj,使之成为当前构象;否则,不接受Sj,则仍使Si为当前构象;
第五步 当达到最大迭代次数时,输出当前能量值最小的构象及其最小能量值;如果不满足停止准则,则重复第二步到第四步。
结果及分析
实验中用真实蛋白质1AEP中的一段氨基酸残基序列作为测试的目标序列,此段序列为:LEU THR ASN VAL GLY HIS GLN TRP GLN ASP ILE ALA THR。将此段残基序列分别用沃氏法、F-P法、埃氏法、KD法以及米氏法转换为亲疏水性的HP模型。采用MC算法分别从序列的正向及其反向搜索其最小能量构象,并求取最小能量值,探讨从序列的正反方向开始搜索,对蛋白质折叠的最小能量值及其构象是否有影响。

表1 描述20种氨基酸残基疏水特性参数

图1 残基走向演示图
序列与最小能量值比较
实验结果表明,在各种疏水性特征参考值下求得最小能量值如表2所示。由此可以看出同一种疏水性特征参考值正向和反向折叠所得的最小能量值相同;不同疏水性特征参考值在同一段氨基酸残基序列下得到的能量最小值存在一定的差异,且相差较大。

图2 序列长度为13个残基的肽链的最小能量的可能构象

表2 序列与最小能量值
最小能量值与其构象比较
各疏水性特征参考值所得到的蛋白质最小能量构象存在一定的差异,同一种疏水性特征参考值正向和反向折叠所得的最小能量构象也存在不同程度的差异,如图3所示。由图3可以看出,氨基酸残基的序列,在不同的疏水性特征参数的影响下,最小能量相差较大。
在寻找最小能量构象时,我们采用的是随机搜索的MC算法。由图3中的(1)和(2)在经过顺时针旋转90°完全相同;沃氏法和K-D法在序列相同的情况下,图3中的(7)、(8)、(9)、(10),在相等的最小能量值下,所寻找到的最小能量构象因随机性的影响,图(7)、(9)、(10)完全相同,与图8存在差异。
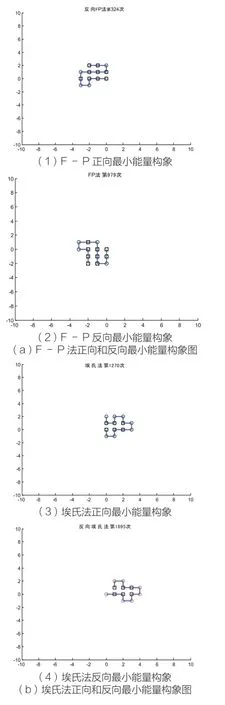


图3 各疏水性特征参数最小能量构象图
由以上结果我们可以大胆的推测,由于蛋白质的折叠是一个高度定向且多因素控制的过程,在仅考虑亲疏水性对蛋白质折叠构象的影响因素上,从序列的正反方向开始折叠,对蛋白质折叠的最小能量及其构象无影响。
结束语
对蛋白质折叠结构的计算机模拟可以很好的解决实验测定蛋白质结构的困难,它将增进我们对蛋白质折叠结构的进一步认识,帮助我们更好的了解结构与功能的关系。模拟的实验结果表明,对于同一列氨基酸残基序列,运用几种常见的对氨基酸残基疏水性特征参考值的不同划分方法,所得到的蛋白质最小能量构象和最小能量值均不相同。人们已经知道,维持蛋白质构象的最小能量越低,其构象越稳定。那么,哪一种疏水性参考值能更好的反应真实蛋白质折叠结构,我们将对其继续进行下一步的研究探索,以期了解更多有关几种常见的对氨基酸残基疏水性特征参考值,对蛋白质结构的维持和稳定影响的大小。

史小红 范倩西安工业大学理学院
10.3969/j.issn.1001-8972.2015.07.001
