基于旋转变换的二值形态算子的研究

段 汕，樊金东，赖国琴，贾梦真，黄 珍

(中南民族大学数学与统计学学院，武汉430074)

数学形态学是一门图像处理与分析的学科，其基本思想是利用一个称之为结构元素的“探针”在图像内部移动，探测收集图像的信息.在二值形态学中，将图像视为集合，结构元素以平移变换的方式在图像内部移动，对于图像内部信息的收集则是通过集合的包含关系(序关系)和集合的交、并、余等运算为主要工具建立的二值形态算子实现的［1-4］.这样意义的二值形态算子也称为平移形态算子.

本文在文献［5］的基础上，将结构元素移动的方式通过平面旋转变换来实现，建立称之为旋转形态算子的相关理论，引入了基于旋转变换的二值形态腐蚀、膨胀、开、闭算子，并对其性质进行了较为详尽地研究.

1 预备知识

考虑E2=R2{0}，其上的点用极坐标(r，θ)表示，其中r＞0是极径，θ是以2π为模的角度(0≤θ＜ 2π)，在 E2上定义点乘运算(r，θ)·(r'，θ')=(rr'，θ+θ')，显然该运算满足交换律.对于集合A⊆E2进行(r，θ)的旋转变换及其逆变换，分别表示为:

旋转变换的全体 T={τr，θ|r ＞ 0，0≤ θ＜ 2π}构成一个Abel群.在文献［5］中，给出了基于T的腐蚀和膨胀:

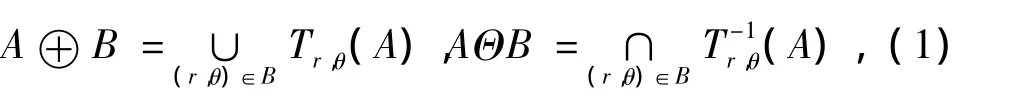
其中A，B⊆E2.对于集合A进行关于b=(r，θ)的旋转变换 τr，θ(A)及其逆变换 τ－1r，θ(A)也可以用点乘运算表示:

2 基于旋转变换的二值腐蚀、膨胀算子的表示及性质

基于旋转的腐蚀、膨胀定义(1)是通过集合的交并运算来描述的，可以证明这种定义方式具有如下的等价代数表示形式.

性质1

性质2

对二值数学形态学而言，腐蚀与膨胀是其基本运算，利用(2)、(3)式可以推导出与平移形态算子类似的性质.

利用平面点乘运算的可交换性，可得出基于旋转变换的二值膨胀满足交换律.

性质3 A⊕B=B⊕A.

性质4 ①A⊕(B⊕C)=(A⊕B)⊕C，②AΘ(B⊕C)=(AΘB)ΘC.

证明 只证②:对∀x∈(AΘB)ΘC，有∀c∈C，x·c∈AΘB，对∀b∈B，有(x·c)·b∈ A，所以x·(b·c)∈ A，x∈ AΘ(B ⊕ C)，故(AΘB)ΘC ⊂AΘ(B⊕C);

对 ∀x1∈AΘ(B ⊕ C)，有 ∀b1∈ B，c1∈ C，x1·(b1·c1)∈ A.所以(x1·c1)·b1∈ A，x∈(AΘB)ΘC，故 AΘ(B ⊕ C)⊂ (AΘB)ΘC，② 式成立.

由性质4可以看出基于旋转变换的二值膨胀满足结合律.

性质5 ①(AΘB)c=Ac⊕，②(A⊕ B)c=AcΘ，其中={|b∈ B}.

证明 ①(AΘB)c={x|x·b∈A，∀b∈B}c={x|B·x⊂A}c={(B·x)∩Ac=∅}c={x|B·x∩Ac≠∅}.A⊕B={x|x=a·b，a∈A，b∈ B}={x|x·∈A，b∈B}={x|x·∩A≠∅，b∈B}={x|(·x)∩A≠∅}.所以Ac⊕={x|(B·x)∩Ac≠ ∅}，即(AΘB)c=Ac⊕.

②(A⊕B)c={x|(·x)∩A≠∅}c={x|(·x)∩A=∅}={x|(·x)⊂Ac}，又AΘB={x|B·x⊂ A}，故{x|(·x)⊂ Ac}=AcΘ，即(A ⊕ B)c=AcΘ.

该性质表明基于旋转变换的二值腐蚀与膨胀满足对偶性.

性质6 ①(A·x)⊕B=(A⊕B)·x，②(A·x)ΘB=(AΘB)·x.

证明 ①(A·x)⊕B=(A⊕{x})⊕B=(A⊕B)⊕{x}=(A⊕B)·x.

② ∀y∈(A·x)ΘB，对∀b∈B，有y·b∈A·x，则 ∃a ∈ A，使得 y·b=a·x，即 y=(a·)·x，所以 y=(a·)·x∈ (AΘB)·x，故(A·x)ΘB ⊂(AΘB)·x;∀y1∈(AΘB)·x，∀b1∈ B，有(y1·)·b1∈A，所以(y1·b1)·∈A，y1∈ (A·x)ΘB，故(AΘB)·x⊂ (A·x)ΘB，即(A·x)ΘB=(AΘB)·x.

此性质说明了基于旋转变换的二值腐蚀、膨胀关于目标对象满足旋转不变性，也可以说，关于目标对象，基于旋转变换的二值腐蚀、膨胀运算与点乘运算是可以交换的.

性质7 ① A⊕ (B·x)=(A⊕ B)·x，②AΘ(B·x)=(AΘB)·.

证明 ①A⊕(B·x)=(B·x)⊕A=(A⊕B)·x.

② AΘ(B·x)=AΘ(B ⊕ {x})=AΘBΘ{x}=∩ {AΘB·|x∈ {x}}=(AΘB)·.

该性质表明基于旋转变换的二值膨胀关于结构元素也满足旋转不变性.

·x)Θ(B·x)=AΘB，其中 x∈ E2.

基于旋转变换的二值膨胀运算，目标对象与结构元素相反方向的旋转不会改变膨胀运算的结果，而基于旋转变换的二值腐蚀运算的结果不会因目标对象与结构元素的同向旋转而改变.

性质9 若单位元(1，0)∈B⊂E2，则 ①AΘB⊂A，②A⊂A⊕B.

证明 ①对∀x∈AΘB，有∀b∈B，x·b∈A，又因为(1，0)∈B，所以 x·(1，0)∈ A，即x∈A，故AΘB⊂A.

② 对∀a∈A，b∈B，有a·b∈A⊕B，又因为(1，0)∈B，所以a·(1，0)∈A⊕B，即a∈A⊕B，故A⊂A⊕B.

从该性质看出当单位元属于结构元素时，基于旋转变换的二值腐蚀是非扩展的，即目标对象经过腐蚀运算后变小，而基于旋转变换的二值腐蚀是满足扩展性的，即膨胀运算会使目标对象变大，这与基于旋转变换的腐蚀、膨胀的定义相对应.

性质10 如果A⊂B，则 ①A⊕C⊂B⊕C，② AΘC⊂BΘC.

证明 ①对∀x∈A⊕C，则∃a∈A，c∈C，使得x=a·c，又A⊂B，所以有a∈B，x∈B⊕C，故A⊕C⊂B⊕C.

② 对∀x∈AΘC，∀c∈C，有x·c∈A，又A⊂B，所以有 x·c∈ B，x∈ BΘC .故 AΘC ⊂BΘC.

此性质说明了基于旋转变换的二值腐蚀、膨胀关于目标对象满足递增性.

性质11 如果B⊂C，则①A⊕B⊂A⊕C，②AΘC⊂AΘB.

证明 ①A⊕B=B⊕A⊂C⊕A=A⊕C.

②对∀x∈AΘC，∀c∈C，有x·c∈A，故对∀b∈B，因为B⊂C，所以b∈C，故x·b∈A.又因为b∈B，所以 x∈ AΘB.故 AΘC⊂ AΘB.

此性质说明基于旋转变换的二值腐蚀与膨胀关于结构元素也满足递增性.

性质12 ① (B∩C)ΘA=(BΘA)∩(CΘA)，②AΘ(B∪C)=(AΘB)∩(AΘC)，③A⊕(B∪C)=(A⊕B)∪(A⊕C).

证明 ① 对 ∀x∈ (B∩ C)ΘA，∀a∈ A，有x·a∈B∩C，即x·a∈B且x·a∈C，所以x∈BΘA且x∈CΘA，即x∈(BΘA)∩(CΘA)，所以(B∩C)ΘA⊂(BΘA)∩(CΘA).

对∀x∈(BΘA)∩(CΘA)，有a1∈A，x∈BΘA且x∈CΘA，使得x·a1∈B∩C即x∈(B∩C)ΘA，所以(BΘA)∩ (CΘA)⊂ (B∩ C)ΘA，即(B∩C)ΘA=(BΘA)∩(CΘA).

②对∀x∈AΘ(B∪C)，对∀y∈B∪C有x·y∈A，y∈B或y∈C.对∀y∈B，x·y∈A，可知x∈AΘB.对∀y∈C，x·y∈A，可知x∈AΘC.故x∈(AΘB) ∩ (AΘC)，AΘ(B ∪ C) ⊂ (AΘB)∩(AΘC).

对 ∀x∈(AΘB)∩(AΘC)，有x∈AΘB且x∈AΘC.对 ∀b∈ B，c∈ C，有x·b∈A，x·c∈A，所以{x·b}∪{x·c}=x·{b∪c}∈A，因为b∪c∈B∪ C，所以 x∈ AΘ(B∪ C)，得(AΘB)∩(AΘC)⊂AΘ(B∪C)，即AΘ(B∪C)=(AΘB)∩(AΘC).

③ A⊕(B∪C)=∪{A·x|x∈B∪C}=［∪{A·x|x∈B］∪［∪{A·x|x∈C}］=(A⊕B)∪(A⊕C).

此性质说明对基于旋转变换的二值腐蚀运算，目标对象求交集运算满足可分解性，对于基于旋转的二值腐蚀、膨胀，结构元素关于求并运算是可分解的.对目标对象或结构元素进行分解，能简化运算对象，提高运算效率［6］.

性质13 ①(AΘC)∪(BΘC)⊂(A∪B)ΘC，② (AΘB)∪(AΘC)⊂AΘ(B∩C).

证明① 对∀x∈(AΘC)∪(BΘC)有x∈AΘC或x∈BΘC.由x∈AΘC和A⊂A∪B有x∈(A∪B)ΘC，所以(AΘC)∪(BΘC)⊂(A∪B)ΘC.

② 对∀x∈(AΘB)∪(AΘC)，有x∈AΘB或x∈AΘC.由x∈AΘB知:对∀b∈B，有x·b∈A，由x∈AΘC知:对∀c∈C，有x·c∈A.即对∀y∈B∩C，有x·y∈A，所以x∈AΘ(B∩C)，故(AΘB)∪(AΘC)⊂AΘ(B∩C).

性质14A⊕(BΘC)⊂(A⊕B)ΘC.

证明 对∀x∈ A⊕ (BΘC)，有 a∈ A，y∈BΘC，使得 x=a·y.对 ∀c∈ C，有 y·c∈ B，所以(y·c)·a∈A⊕B，即(y·a)·c∈A⊕B.故y·a∈(A⊕B)ΘC，即x∈(A⊕B)ΘC，所以A⊕(B⊕C)⊂(A⊕B)ΘC.

性质15 A⊂BΘC⇔A⊕C⊂B.

证明 对∀x∈A⊕C，有a∈A，c∈C，使得x=a·c.又A⊂BΘC，所以a∈BΘC，故对∀c∈C，有 a·c∈B.又c∈C，所以a·c∈B，即x∈B，从而A⊕C⊂B.

对于∀a1∈A，c1∈C，有a1·c1∈A⊕C，又A⊕C⊂B，所以 a1·c1∈ B，又 c1∈ C，所以 a1∈BΘC，故 A⊂ BΘC.

该性质表明基于旋转变换的腐蚀和膨胀构成一对附益算子.

3 基于旋转变换的二值开、闭算子的表示及性质

在E2中，给定集合A，B，将B对A先腐蚀后膨胀的运算称为B对A的开运算，记为A·B，即A·B=(AΘB)⊕B.将B对A先膨胀后腐蚀的运算称为B对A的闭运算，记为A·B，即A·B=(A⊕B)ΘB.利用前面已证明的性质，可以推导出以下基于旋转变换的开、闭算子的基本性质.

性质16 A·B=∪{B·x|B·x⊂A}，其中x∈AΘB.

证明 对∀y∈(AΘB)⊕B，∃x∈AΘB，b∈B，使得 y=x·b，对 ∀b1∈ B，有x·b1∈ A，又 b∈B，所以 x·b∈A，即y=x·b∈A，y∈∪{b·x，b∈B}，y∈∪{B·x|B·x⊂A}，即(A·B)⊂∪{B·x|B·x⊂A}.

对 ∀y∈∪{B·x|B·x⊂A}，有y∈B·x⊂A，所以对 ∀b∈B，有b·x∈A，所以x∈AΘB.又∀y∈∪{B·x|B·x⊂A}，∃b1∈B，使得y=b1·x，所以y∈(AΘB)⊕B，即y∈A·B，所以∪{B·x|B·x⊂A}⊂(A·B)，即A·B=∪{B·x|B·x⊂A}.

目标对象A作基于旋转的开运算后所得的集合是其本身的子集.由此性质可以直观地理解基于旋转的开运算的效果:B·x就是相当于旋转结构元素，将结构元素B放入集合A当中，不断地旋转结构元素B，结构元素B所能达到的所有区域的并集就是利用结构元素B对集合A作开运算的结果.此性质提供了一种实现基于旋转的开运算的算法［7］.

性质17 (A·B)c=Ac·，(A·B)c=Ac·，其中={|b∈B}.

证明 由性质5有:

(A·B)c=［(AΘB)⊕B］c=(AΘB)cΘ=(Ac⊕)Θ=Ac·.

(A·B)c=［(A⊕ B)ΘB］c=(A⊕ B)c⊕=(AcΘ)⊕=Ac·.

基于旋转变换的二值腐蚀、膨胀满足对偶性.二值开、闭是腐蚀、膨胀的复合运算，因此基于旋转变换的二值开、闭也满足对偶性.

性质18(A·x)·B=(A·B)·x，(A·x)·B=(A·B)·x，其中 x ∈ E2.

证明 由性质6有:

(A·x)·B=［(A·x)ΘB］⊕B=［(AΘB)·x］⊕B=［(AΘB)⊕ B］·x=(A·B)·x.

(A·x)·B=［(A·x)⊕ B］ΘB=［(A⊕ B)·x］ΘB=［(A ⊕ B)ΘB］·x=(A·B)·x.

该性质表明基于旋转变换的二值开、闭运算关于目标对象满足旋转不变性，即关于目标对象，基于旋转变换的二值开、闭运算与旋转运算是可交换的.

性质19A·(B·x)=A·B，A·(B·x)=A·B，其中 x∈ E2.

证明 A·(B·x)=［AΘ(B·x)］⊕(B·x)=［(AΘB)·］⊕(B·x)=(B·x)⊕［(AΘB)·］=B⊕(AΘB)=(AΘB)⊕B=A·B.

A·(B·x)=［A⊕(B·x)］Θ(B·x)=［(A⊕ B)·x］Θ(B·x)={［(A ⊕ B)·x］ΘB}·={［(A⊕B)ΘB］·x}·=A·B.

此性质说明在旋转变换下，结构元素的位置变化不会对开运算或闭运算的结果产生影响.只要结构元素的类型和大小一定，不管结构元素的位置，开、闭运算的结果都是确定的.这与腐蚀和膨胀的运算不一样，腐蚀和膨胀的运算结果和结构元素的位置有密切的关系.结构元素是否包含单位元，腐蚀和膨胀的结果是不一样的［8］.

性质20 A·B⊂A，A⊂A·B.

证明 对∀x∈(AΘB)⊕B，∃x1∈AΘB，b1∈ B，使得 x=x1·b1.对 ∀b∈ B，有 x1·b∈ A，又b1∈ B，所以 x1·b1∈A，即x∈ A，故 A·B ⊂A.

对∀a∈A，b∈B，有a·b∈A⊕B，又b∈B，有a∈(A⊕B)ΘB，即a∈A·B，故A⊂A·B.

这个性质表明基于旋转变换的二值形态开运算是非扩展的，而基于旋转的二值闭运算是扩展的.

性质21 如果A⊂B，则A·C⊂B·C，A·C⊂B·C.

证明 因为A⊂B，由性质11有AΘC⊂BΘC，(AΘC)⊕C⊂(BΘC)⊕C，即A·C⊂B·C.

因为A⊂B，由性质11有A⊕C⊂B⊕C，(A⊕C)ΘC⊂(B⊕C)ΘC，即A·C⊂B·C.

该性质说明基于旋转变换的二值开、闭运算关于目标对象满足递增性.

性质22AΘB=(A·B)ΘB=(AΘB)·B.

证明 令A1=AΘB，A2=A1⊕B，A3=A2ΘB.由A1=AΘB可知A1⊂AΘB，由性质A⊂BΘC⇔A⊕C ⊂B，有A1⊕B⊂A，即A2⊂A.由A2=A1⊕B有A1⊕B⊂A2，同时有A1⊂A2ΘB，即A1⊂A3.由A2⊂A和性质11可得A2ΘB⊂AΘB，即A3⊂A1，所以有A1=A3，即 AΘB=A2ΘB=(A1⊕ B)ΘB=［(AΘB)⊕B］ΘB=(A·B)ΘB.

AΘB=［(AΘB)⊕Β］ΘB=(AΘB)⊕BΘB=(AΘB)·B.

此性质给出了基于旋转变换的二值腐蚀的两种等价运算.

性质23A⊕B=(A⊕B)·B=(A·B)⊕B.

证明 令A1=A⊕B，A2=A1ΘB，A3=A2⊕B.由A1=A⊕ B可知 A⊕ B⊂ A1，由性质 A⊂BΘC⇔A⊕C⊂B得A⊂A1ΘB，即A⊂A2.由A2=A1ΘB有 A2⊂ A1ΘB.同时有 A2⊕ B ⊂ A1，即 A3⊂A1.又A⊂A2和性质11可得A⊕B⊂A2⊕B，即A1⊂ A3，所以有A1=A3，故A⊕B=A2⊕B，A⊕B=(A1ΘB)⊕B=(A·B)⊕B，即A⊕B=(A⊕B)·B=(A·B)⊕B.

该性质给出了基于旋转变换的二值膨胀的两种形式.

性质 24A·B=(A·B)·B，A·B=(A·B)·B.

证明 由性质22得(AΘB)⊕ B=［(A·B)ΘB］⊕B，即A·B=(A·B)·B.

由性质23得A⊕B=(A·B)⊕B，(A⊕B)ΘB=［(A·B)⊕ B］ΘB，即 A·B=(A·B)·B.

该性质表明了基于旋转变换的二值开、闭运算满足等幂性，即用同一个结构元素对原集合作两次(或两次以上)的开运算(或闭运算)得到的结果与用此结构元素作一次运算的结果相同.

4 结束语

本文从二值形态学入手，将结构元素移动的方式通过平面旋转变换来实现，给出基于旋转变换下的二值形态腐蚀、膨胀、开、闭算子的等价表示形式，并研究了旋转变换下的相关性质.研究结果表明:旋转形态算子保留了平移形态算子诸如对偶性、等幂性、附益性等基本性质.

［1］崔 屹.图像处理与分析数学形态学方法及应用［M］.北京:科学出版社，2000:1-86.

［2］唐常青，吕宏伯，黄 铮.数学形态学方法及其应用［M］.北京:科学出版社，1990:1-31.

［3］向朝森，段 汕.基于二值形态学的形态变换方法及应用［D］.武汉:中南民族大学，2011.

［4］段 汕，梅建新.基于数学形态学的图像处理方法［J］.中南民族大学学报:自然科学版，2003，22(4):67-70.

［5］Heijmans H.Morphological image operators［M］.Boston:Academic Press，1994:147-149.

［6］段 汕，向朝森.本影变换与灰值形态变换［J］.中南民族大学学报:自然科学版，2010(1):111-114.

［7］段 汕，梅建新，秦前清.基于不同代数结构的图像形态滤波［J］.湖北大学学报:自然科学版，2003(4):283-286.

［8］王 坤，高立群，郭 丽，等.多尺度结构元素的数学形态学边缘检测新方法［J］.东北大学学报:自然科学版，2008(4):473-476.