机器人辅助的三维点云自动配准

孙 威 黄 惠

（中国科学院深圳先进技术研究院 深圳 518055）

机器人辅助的三维点云自动配准

孙 威 黄 惠

（中国科学院深圳先进技术研究院 深圳 518055）

针对三维扫描时不同扫描仪坐标系下三维点云配准困难且耗时过多的难题，提出一种利用机器人转换扫描仪坐标来进行点云配准的算法。该算法主要有两步：第一步为粗配准，将三维扫描仪固定在服务机器人的机械臂末端，在三维扫描过程中实时记录扫描仪的姿势，并利用此信息将不同扫描仪坐标系的点云转换到机器人基底坐标系；第二步为精细配准，以第一步的结果作为改进的迭代最近点算法的初始值，再利用加权的稀疏迭代最近点算法对机器人基底坐标系下不同帧的点云进行精细配准。实验证明，相比其他基于仪器的配准方法和直接利用迭代最近点算法进行配准的方法，该方法能有效提高配准成功率、减少配准时间、提高配准精度。

点云配准；迭代最近点算法；坐标变换；三维扫描；机器人

1 引 言

近年来，三维激光扫描仪的快速发展使得获取真实场景的高精度三维点云越来越便利，对真实场景进行三维扫描和重建得到了越来越多的关注。通常进行三维扫描时，扫描一次只能得到被扫描物体在扫描仪视野范围内的点云数据。要想得到整个物体完整的几何形状信息，需要从多个视角进行扫描。由于在不同视角下进行扫描时的参考坐标系不同，为了得到物体整个表面的完整点云数据，必须将多个视角下得到的点云配准到同一个坐标系。

目前，三维点云配准主要有手动配准、基于仪器的配准和自动配准［1］三种方法。其中，后两种方法较为常用。基于仪器的配准方法通过计算扫描系统硬件的坐标关系将多帧点云转换到同一坐标系下，该方法不依赖于点云的特征，配准速度快，但对系统硬件的设计搭建具有较高要求。自动配准也就是直接利用诸如迭代最近点［2］及其各种改进算法［3，4］进行配准，要求要配准的两帧点云数据有足够的重叠区域（共同特征）来确定初始对应点集。而在实际应用中，这样的要求往往以牺牲扫描效率为代价，甚至可能无法完成对物体的完整扫描。例如，在基于最佳下一视角［6-9］的自动扫描中，往往需要配准的两帧点云数据之间很可能只有较小的重叠区域甚至没有重叠的区域。在这种情况下，就需要一个粗配准的方法将不同坐标系下的点云转换到同一坐标系下。现有的粗配准方法主要有基于旋转平台的方法［10-12］，基于标志点的方法，基于扫描物体曲面特征的方法［13］等。但这些传统的方法往往很难满足精度要求，不能为随后的精细配准算法提供良好的初始值。大部分基于旋转平台的方法，主要利用计算机视觉中的轮廓线重构方法或序列影像重构方法，而这些方法中对旋转平台进行标定的方法一般都是从图像中提取标定物的特征平面，再根据平面相交于旋转轴的约束条件进行参数的求解。这些方向需要特征提取的步骤并且还需要标定相机的步骤。此外，利用转台扫描模型对复杂模型的顶部和底部的扫描和配准比较困难。而基于标志点的方法，需要往扫描物体上贴大量标签，当进行大规模物体扫描或被扫描物体表面几何特征比较复杂时，该方法效率低下且配准精度较低。

针对上述问题，本文提出一种利用机器人辅助快速进行点云数据配准的自动化方法：利用机器人记录扫描仪位姿信息（包含旋转矩阵 R 和平移矢量 t）并将其用于粗配准，将粗配准所获得的结果作为加权的稀疏迭代最近点算法［5］的初始值，完成点云数据间的精确配准［14］。

2 机器人辅助的点云粗配准

本文所用的机器人为 PR2 机器人（图1）。PR2 来自专业的机器人研发公司 Willow Garage，被称为全球首个可完成综合性操作的智能机器人。PR2 是下一代家庭服务机器人的雏形，在其头部、颈部、肘部、钳子上分别安装有深度摄像头、激光测距仪、高分辨率摄像头、触觉传感器等丰富的传感设备。PR2 的底部有两台8 核电脑作为机器人各硬件的控制和通讯中枢，并安装有Ubuntu 和 Robot Operating System。PR2 依靠底部的四个轮子移动；其有两条手臂，每条手臂七个关节，手臂末端是一个可以张合的钳子。

图1 本文提出的三维扫描系统Fig. 1 The proposed 3D scanning system

在本文的三维扫描系统中，三维扫描仪固定在机器人手臂的末端，并将其固定的位置添加到机器人的描述文件当中，固定之后扫描仪成为整个机器人系统的一部分。我们在机器人底部中心位置建立如图2 的基底坐标系，根据机器人描述文件中定义的机器人各关节相对位置，就可以获得机器人各关节的坐标系之间的关系，也即可以实时获取不同视角下扫描仪坐标系与机器人基底坐标系之间的转换关系。

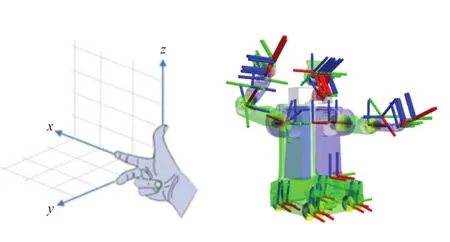
图2 机器人坐标系Fig. 2 The robot coordinate system

在扫描仪坐标系 S 下，记点云数据 PS，根据机器人扫描仪坐标系 S 与机器人基底坐标系 B 之间的转换关系 ，可得在机器人基底坐标系 B下的点云数据为：

对不同视角 i（i = 0， … ， n）下扫描得到的所有点云数据均做如上的变换即能将点云 PSi统一到机器人基底坐标系 B 下：

由于机器人定位精度、运动抖动等因素的影响，利用机器人转化坐标的配准方法无法确保较高的精度。这一粗配准得到的结果在两组点云的重叠部分容易出现匹配不准的现象。为解决这一精细配准的问题，本文采用了改进的稀疏迭代最近点算法来进行优化。

3 精细配准算法

3.1 经典的迭代最近点算法

用集合 P 和 X 分别表示点云 pi和 xi的集合。其中，集合 P 中点的个数为 NP；X 中点的个数为NX。迭代最近点算法（Iterative Closest Point，ICP）本质上是基于二乘法的最优匹配方法，是一个不断进行原始数据与旋转平移数据反复迭代替换的过程，最终要达到一个匹配正确的收敛状态。该算法的根本目的是得到点云间的刚体变换，并用矢量表示，使得误差函数

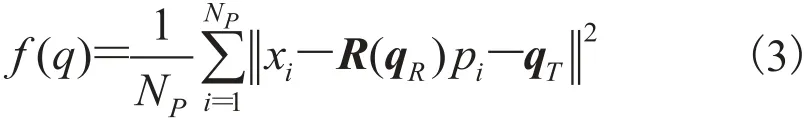
最小。其中，qR为用四元数表示的旋转变换；qT表示刚体变换的平移变换；R（qR）表示将四元数qR转换为旋转矩阵。

经典 ICP 算法描述如下：

初始迭代时，设点云初始位置为 ，当前迭代次数 时，迭代执行如下步骤，直到目标函数收敛于给定的阈值 ：

①由当时点云初始位置，利用公式（ 3 ）计算最近点点集 Yk；

②在 Yk基础上，计算配准向量（qk，dk），其中，qk代表平移分量，dk代表旋转分量；

④如果满足给定的误差阈值，即 ，则终止迭代，否则 ，并执行①。

3.2 改进的稀疏迭代最近点算法

Li 等［13］提出了稀疏 ICP 算法，用稀疏范数p-norms 来替换原来的 2-范数，获得了比传统ICP 算法更好的配准效果。该法将经典 ICP 问题转化为：

其中，p∈［0， 1］；R 为旋转矩阵；t 为平移向量；x 为源点云数据中的点；y 为目标点云数据中的点。两帧点云数据之间转换的刚性通过将旋转矩阵 R 约束到特殊正交群 SO（k）来确保，这一约束利用指示函数 IA（b）实现。当 b∈A 时，指示函数IA（b）=0；其他情况下，IA（b）接近于正无穷。

但其改进后的 ICP 仍然是一种局部优化算法，不能保证收敛到全局最优解，只有当点云的初始相对位置接近真实的位置时，ICP 算法才能得到真实的全局配准。因为粗配准方法已经能保证两帧点云的初始相对位姿接近真实位置了，所以稀疏 ICP 算法比较适合本文所述的精细配准过程。与此同时，为了提高算法的运算效果，本文对该算法提出一些改进措施。

通过给对应点赋予权值的方法来剔除无效点对，即剔除权值大于给定阈值的点对。传统的ICP 算法中，在搜索最近点时须计算每个点，因为点云中的每个点都有相同的权重，这一设定降低了 ICP 算法的效率。本文对点云中的对应点采用权重策略采样［15］，点对的距离越远，赋给它的权值 w 越小。

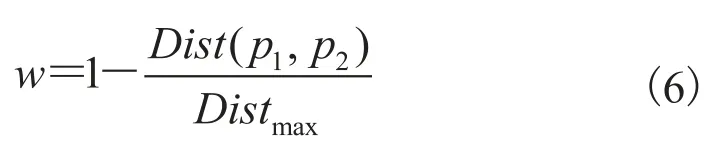
其中，表示对应点间的欧式距离； 表示对应点距离的最大值。由公式（6）可对每个对应点赋予不同的权值。

4 算法流程图

如图3 所示，整个算法的流程如下：每次扫描仪完成扫描后，实验平台与机器人利用 socket进行通信，将得到的点云数据转换到机器人基底坐标系下，再采用改进的稀疏 ICP 算法对点云进行精细配准。由于扫描通常得到是含有稀疏噪声的点云数据，有可能严重干扰配准结果使之陷入局部极值。此外，每帧点云的数据量通常都很大，为后续配准计算所需空间以及时间带来了巨大的负担。因此，为了能够加快配准算法的精度和计算速度，在进行粗配准之前，对点云进行降采样和去噪预处理工作。

采用距离统计去噪音法，是通过对点云中每个点的邻近点进行欧式距离统计，利用统计得到的距离信息去除那些局外的噪声点［16］。该方法的主要思路是使用 k 近邻搜索邻点，k为设定值。对每一个点，计算该点到它的所有邻点的平均距离和标准差。假设点云符合一个给定平均值 α 和标准差 σ 的高斯分布，该平均值 α 和标准差 σ 由点的全局平均距离决定。如果一个点到所有相邻点的平均距离和标准差分别超过了 α 和 σ，则被视为噪声点，即被移除。

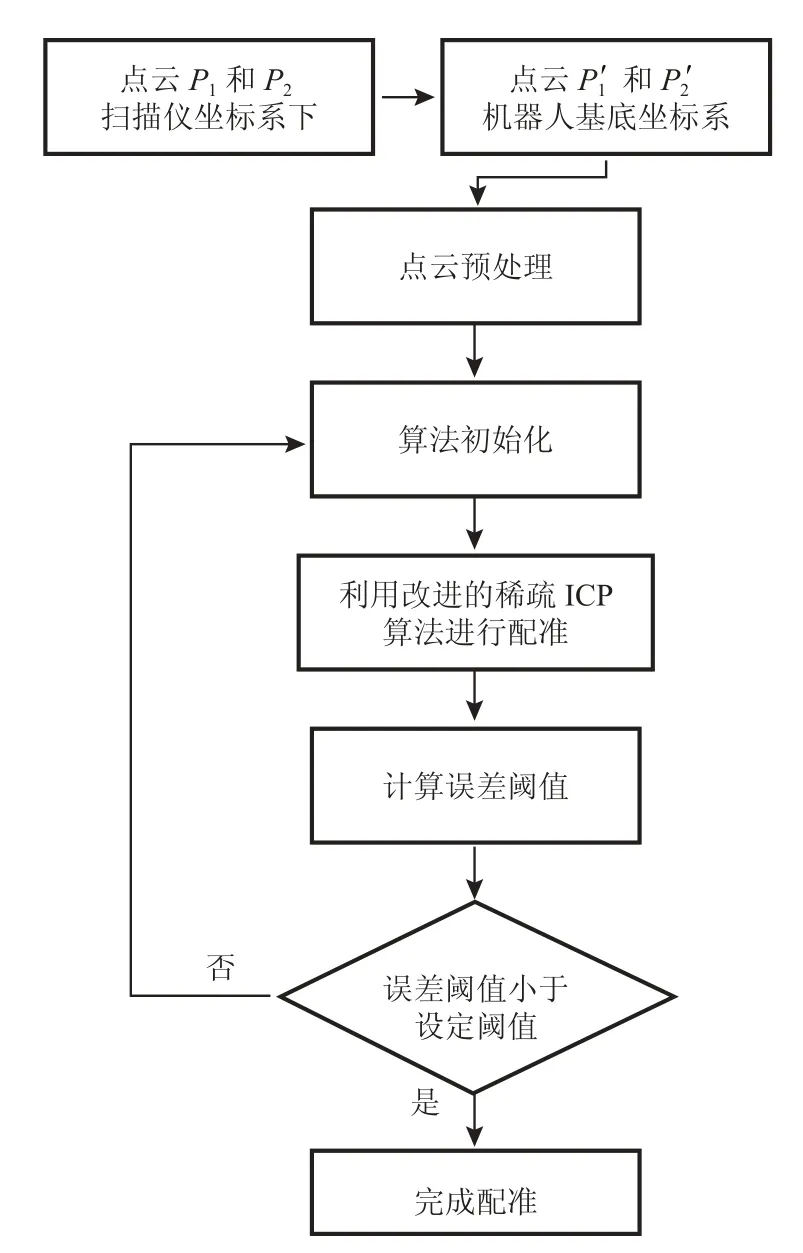
图3 算法的流程图Fig. 3 The flow chart of the proposed method

本文采用均匀降采样算法［17］来保证输入数据的相对密度和形状不变。对输入原始点云中的每个点，在其邻域内搜索 k 近邻点，去除这些邻近点以实现均匀降采样。该方法的关键在于如何确定查找 k 近邻时的搜索范围以及尽可能最小化该搜索范围以节约时间，提高效率。本文将 k-d 树［18，19］用于对点云中的点进行最近邻搜索。k-d 树是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的二叉树结构。k-d 树沿着垂直于相应轴线的超平面把空间划分为不同的子空间，并将所有非叶子节点分割到特定维。在 k-d 树中为每个点进行 k 近邻搜索，找到 k 个最近的点并去除。即每 k 个点中只保留一个点，数据量缩小为原始数据的 1/k 倍。

5 实验结果及分析

5.1 结果

根据本文提出的方法，进行了多个实验以证明该方法的有效性和鲁棒性。

图4、5 和 6 显示了本算法处理一些数据集的中间结果。图4 显示了去噪前后的数据，噪声（4（a）中间的红色区域）被移除。图5 显示了本算法点云降采样前后的数据。可以看到，降采样后的点云数据密度更均匀。图6 显示了机器人辅助的点云粗配准的结果，可以看到，变换坐标系后，两帧点云数据的位置已经比较接近，为后续的改进稀疏 ICP 算法提供了良好的初始值。

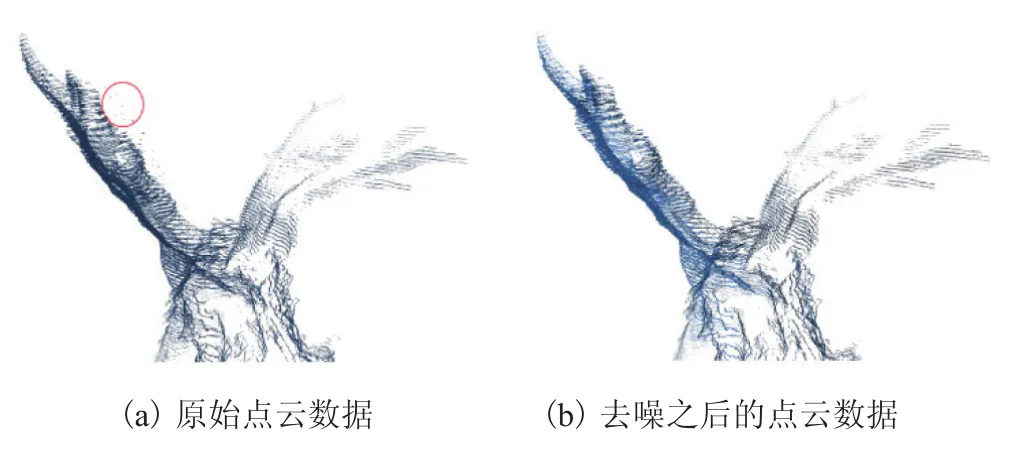
图4 点云去噪前后对比Fig.4The comparison between the raw point clouds and the data processed by outliers removal algorithm

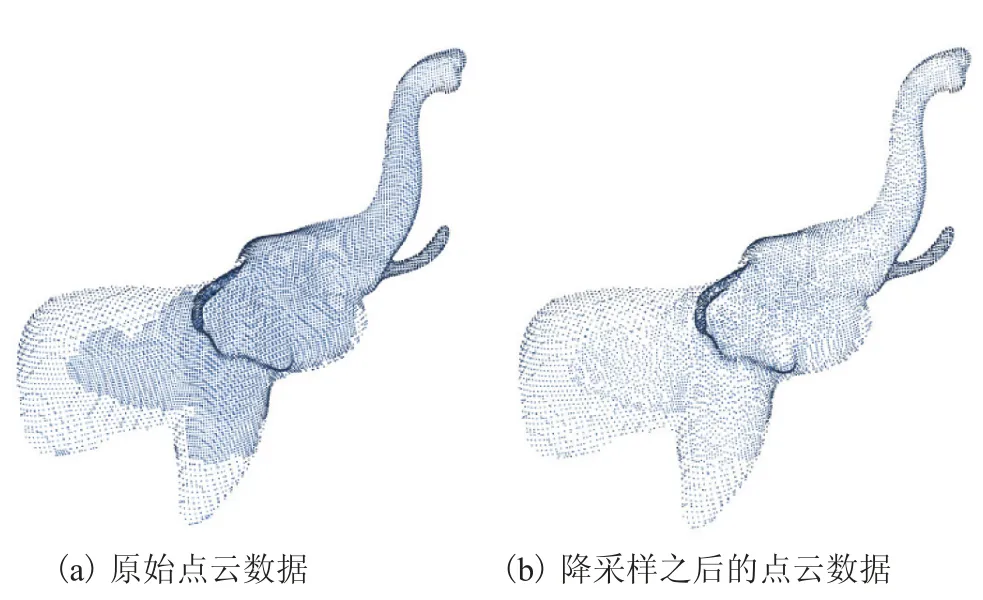
图5 点云降采样前后对比Fig. 5 The comparison between the raw point clouds and the downsample by outliers removal algorithm

图6 机器人辅助转换前后的两帧点云数据Fig. 6 The comparison between the point clouds data before and after transformation with robot-assisted

图7、8 和 9 对比了本文提出的算法与以往算法对两帧或多帧点云进行配准的结果。7（a）、8（a）和 9（a）显示了对模型进行三维扫描得到的数据。首先将机器人辅助的粗配准结果与目前常用的基于主成分分析［20］的初始配准方法进行了比较，如图7（b）（c）、8（b）（c）、9（b）（c）所示。可见主成分分析法无法达到令人满意的配准精度。随后，对比了使用经典 ICP 算法［2］进行精细配准和利用改进的稀疏 ICP 进行精细配准，结果如图7（d）（e）、8（d）（e）、9（d）（e）所示。可以观察到狮子的尾部、小提琴琴弓处、赛亚人模型的脸部均出现了分叉的现象，从对比中可以看出本文的方法能得到更为准确的结果。

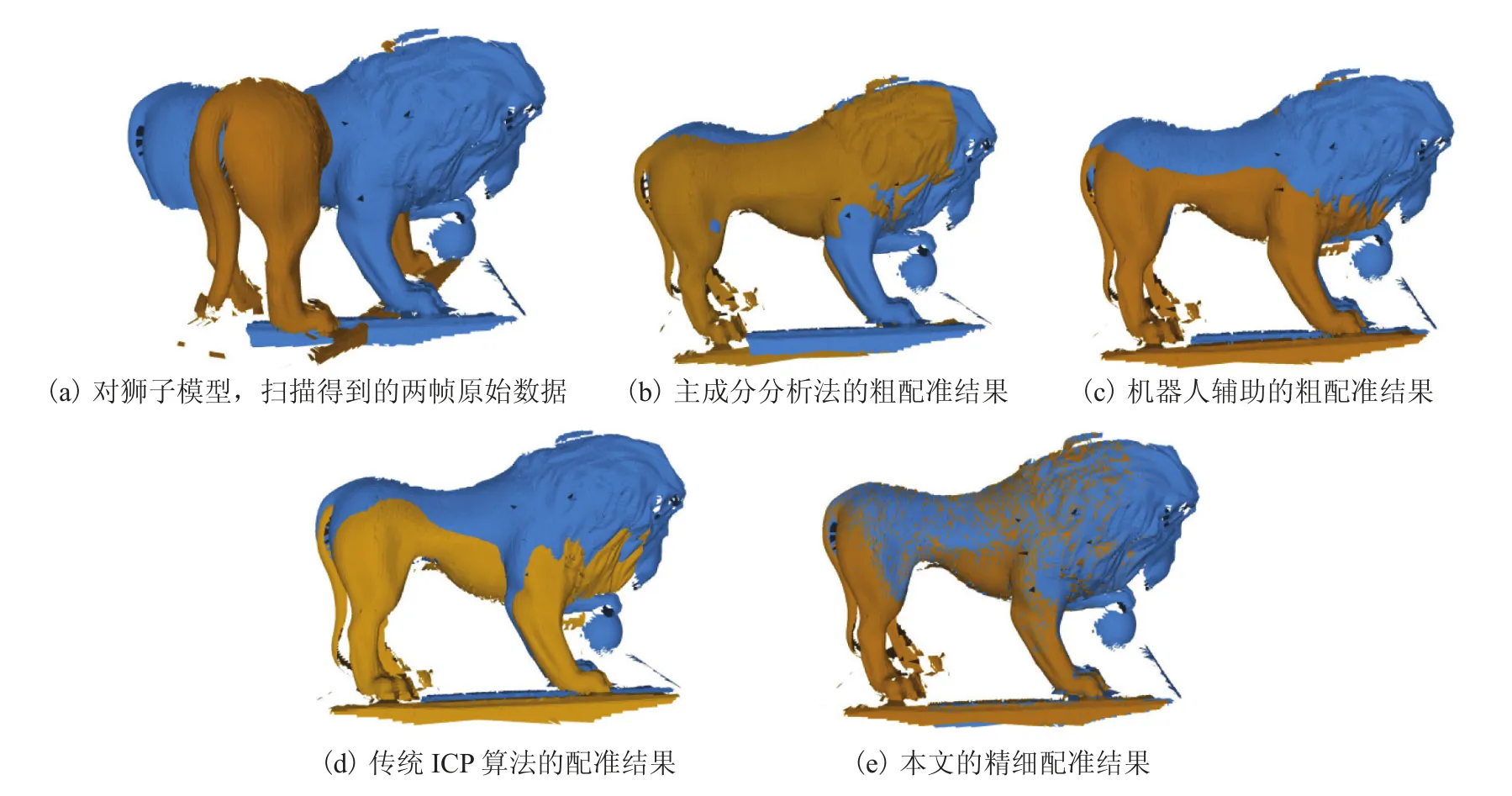
图7 狮子模型的配准结果及对比Fig. 7 The registration result and comparison with other methods of the lion model

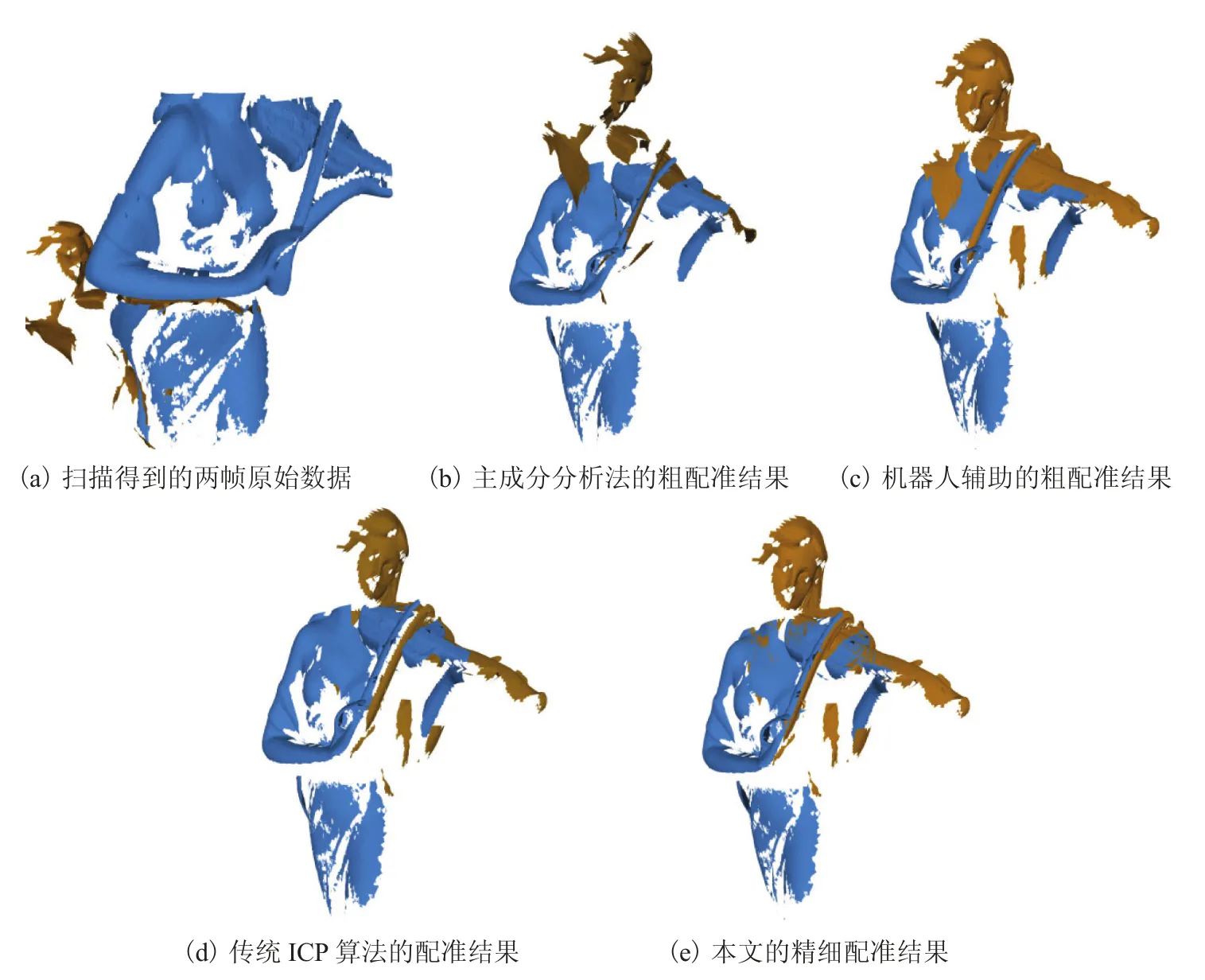
图8 拉小提琴的女人模型的配准结果及对比Fig.8 The registration result and comparison with other methods of the violin woman model

此外，如图10 所示，对于特征较少的点云数据（图10（a）），无论是经典 ICP 算法还是各种改进的 ICP 算法（图10（b））都很容易陷入局部极值而无法获得较好的配准结果，但利用本文提出的方法可以得到较高精度的配准结果（图10（c））。由此可见，即使两帧点云数据之间的重叠区域很小，本文提出的方法也能较为精确地对两帧点云进行配准。

5.2 分 析

为了比较不同算法的配准精度，引入配准精度度量 ε：

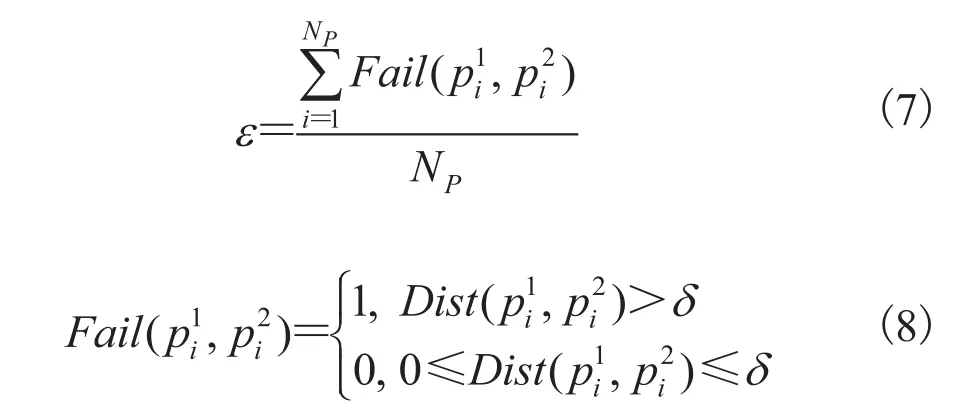
其中，表示配准后两帧点云中对应点对的距离； 表示给定的精度；表示该点对未达到给定的精度要求，NP为点云数量；ε 表示整个点云中未达到精度要求的点所占比例。

为了比较不同算法的速度，我们记录了不同算法的配准时间。所有时间数据均在 Microsoft Windows 7 操作系统，Intel Xeon CPU E5-2637@ 3.50 GHz，32 G 内存的图形工作站作为运行平台测试得到。

表1 记录了包括传统 ICP 算法、稀疏 ICP 算法以及本文算法在配准精度和耗时的统计数据。由表可知，与直接使用 ICP 算法相比，本文所提出方法进行配准的计算时间更短，配准精度更高。

6 总 结

图9 赛亚人模型的 17 帧点云数据配准结果及对比Fig. 9 The registration result and comparison with other methods of the Saiya model （included 17 frames point clouds）

图10 盒子模型的配准结果及对比Fig. 10 The registration result and comparison with other methods of the box model

本文提出了一种机器人辅助的三维点云自动配准算法。首先，结合机器人自动记录扫描仪姿态信息的特性解决了初始配准的问题，然后在稀疏 ICP 算法基础上，通过施加对应点对的权重值以降低算法的执行时间。本文提出的方法能解决点云具有较少共同特征时的配准问题，且比直接使用 ICP 算法进行配准的计算时间要短，配准精度更高。由多个实验结果可以证明，该算法在配准精度和收敛性能上比直接使用 ICP 的配准方法有较大的提高且具有良好的实时性。由于只需进行一次坐标转换，本文的方法耗时更短，可以达到实时粗配准的效果。

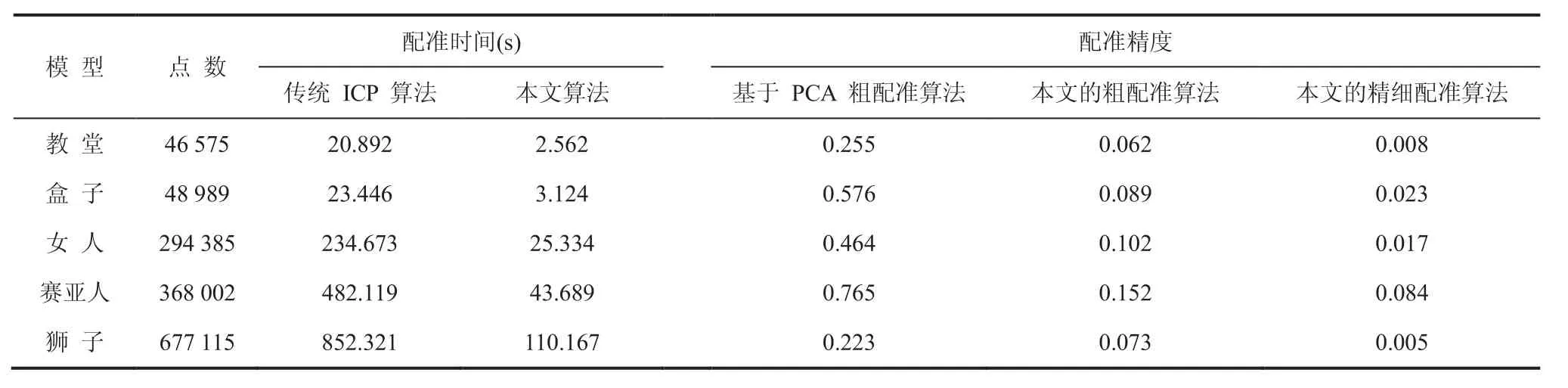
表1 本文配准算法和其他粗配准方法及原始 ICP 算法性能比较Table 1 The comparison between the registration algorithm proposed in this paper and other coarse registration and classical ICP algorithm

本文提出的方法还存在一定的局限性。例如，需要比较精确地标定扫描仪与机器人手臂末端的位置关系。但是，本系统一旦准确标定完成后，就不需要其他人工干预完成，可以自动进行扫描—粗配准—精细配准的整个三维扫描过程。该方法十分便捷，非常适合工具零件、玩具公仔、模型手办和馆藏文物等物品的自动精细快速三维建模，具有较强的实用价值。

［1］ Makadia A，Patterson A，Daniilidis K.Fully automatic registration of 3D point clouds ［C］ // The 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2006：1297-1304.

［2］ Besl PJ，McKay HD.A method for registration of 3-D shapes ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（2）：239-256.

［3］ Rusinkiewicz S，Levoy M.Efficient variants of the ICP algorithm ［C］ // Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling，2001：145-152.

［4］ 戴静兰， 陈志杨， 叶修梓. ICP 算法在点云配准中的应用 ［J］. 中国图象图形学报， 2007，12（3）：517-521.

［5］ Bouaziz S，Tagliasacchi A，Pauly M.Sparse iterative closest point ［J］. Computer Graphics Forum，2013，32（5）：113-123.

［6］ Wu S，Sun W，Long P，et al.Quality-driven poissonguided autoscanning ［J］ // ACM Transactions on Graphics，2014，33（6）：1-12.

［7］ Banta JE，Levine JA， Dumont C， et al. A nextbest-view system for autonomous 3D object reconstruction ［J］. IEEE Transactions on Systems，Man and Cybernetics，Part A：System and Humans，2000，30（5）： 589-598.

［8］ Blaer PS，Allen PK. Data acquisition and view planning for 3-D modeling tasks ［C］ // IEEE/RSJ International Conference on Intelligent Robots and Systems，2007：417-422.

［9］ Connolly C.The determination of next best views［C］ // Proceedings of 1985 IEEE International Conference on Robotics and Automation， 1985：432-435.

［10］ Sadlo F，Weyrich T，Peikert R，et al.A practical structured light acquisition systemfor point-based geometry and texture ［C］ // Proceedings of the Second Eurographics/IEEE VGTL Conference on Point-Based Graphics，2005：89-98.

［11］ Zhang L，Alemzadeh K.A dental vision system for accurate 3D tooth modeling ［C］ //Proceedings of the 28th IEEE-EMBS Annual International Conference on Engineering in Medicine and Biology Society，2006：4799-4802.

［12］ Park SY，Subbarao M.A multiview 3-D modeling system based on stereo vision techniques ［J］. Mach Vision and Application， 2005， 16（3）： 148-156.

［13］ Li X，Guskov I.Multi-scale features for approximate alignment of point-based surfaces ［C］ // Proceedings of the 3rd Eurographics Symposium on Geometry Processing，2005：217-226.

［14］ Gelfand N，Mitra NJ，Guibas LJ，et al. Robust global registration ［C］ // Proceedings of the Third Eurographics Symposium on Geometry Processing，2005： 5.

［15］ Godin G，Rioux M，Baribeau R.Three-dimensional registration using range and intensity information［C］ // Photonics for Industrial Applications，1994：279-290.

［16］ Sotoodeh S.Outlier detection in laser scanner point clouds ［J］. International Archives of Photogrammetry，Remote Sensing and Spatial Information Sciences， 2006，36（5）：297-302.

［17］ Gelfand N，Ikemoto L，Rusinkiewicz S，et al. Geometrically stable sampling for the ICP algorithm［C］ // Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling，2003： 260-267.

［18］ O'Leary G. KdTree search ［EB/OL］.［2015-6-21］.http：//pointclouds.org/documentation/tutorials/.

［19］ Nüchter A，Lingemann K，Hertzberg J.Cached k-d tree search for ICP algorithms ［C］ // Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling，2007：419-426.

［20］ 钟莹， 刘丰华. 复杂模型三维点云自动配准技术的研究 ［J］. 世界科技研究与发展， 2014，36（2）：120-123.

Robot-Assisted Automatic Registration of Three Dimensional Point Clouds

SUN Wei HUANG Hui

（ Shenzhen Institutes of Advanced Technology， Chinese Academy of Sciences， Shenzhen 518055， China ）

Automatic registration of point clouds is a challenging task especially when the overlap between them is too small to initialize the traditional iterative closest point algorithm directly. A method for registering 3D point clouds in different coordinates was proposed by using the scanner's pose information， recorded by a robot. This method consisted of two steps： firstly， 3D scanner was set on the end effector of the robot，which recorded the 6D pose of the scanner when an object was scanned in real time. Using this recorded pose information， the captured point clouds from different scanner coordinates were transformed to robot base coordinate. Secondly， the weighted sparse iterative closest point was used to align the point clouds in robot base coordinate which refines the result of the first step. This method was tested on various data and situations. The experiment results show that the proposed method could align point clouds with lower overlapping ratio，and is more accurate， faster and more robust to outliers than existing methods.

point cloud registration； iterative closest point algorithm； coordinate transformation； 3D scanning； robot

TP 301

A

2015-06-13

2015-06-23

国家自然科学基金（61379091）；科技部863 项目（2015AA016401）；深圳市可视计算与可视分析重点实验室（CXB201104220029A）；深圳市基础研究项目（JCYJ20140901003939034， JCYJ20140901003938994）

孙威，硕士研究生，研究方向为计算机图形学；黄惠（通讯作者），研究员，博士生导师，研究方向为计算机图形、图像处理和科学计算，E-mail：hui.huang@siat.ac.cn。