Agricultural Production Structure Adjustment Scheme Evaluation and Selection Based on DEA Model for Punjab (Pakistan)

Zeeshan　Ahmad,　and　Meng　Jun

College　of　Economics　and　Management,　Northeast　Agricultural　University,　Harbin　150030,　China

Agricultural Production Structure Adjustment Scheme Evaluation and Selection Based on DEA Model for Punjab (Pakistan)

ZeeshanAhmad,andMengJun*

CollegeofEconomicsandManagement,NortheastAgriculturalUniversity,Harbin150030,China

DEAisanonparametricmethodusedinoperationresearchesandeconomicsfieldsfortheevaluationoftheproduction frontier.Ithasdistinctintrinsicwhichisworthcopingwithassessmentproblemswithmultipleinputsinparticularwithmultiple outputs.ThispaperusedDεC2RmodelofDEAtoassessthecomparativeefficiencyofthemultipleschemesofagriculturalindustrial structure,attheendwechosethemostfavorablealsoknownas"OPTIMAL"scheme.Inadditiontothis,usingsomefunctional insightsfromDEAmodelnonoptimalschemesorlessoptimalschemeshadalsobeenimprovedtosomeextent.Assessmentand selectionofoptimalschemesofagriculturalindustrialstructureusingDEAmodelgaveagreaterandbetterinsightofagricultural industrialstructureandwasthefirstofsuchresearchesinPakistan.

agriculturalindustrialstructureadjustment,agriculturalproductionstructure,linearprogramming,DEA,punjab

Introduction

Dataenvelopmentanalysis(DEA)isalatestresearch area,whichinrealityisacombinationofoperational research,managementsciencesandeconometrics (CharnesandCooper,1978).Sincethen,ithadbeen usedindifferentcountriesasaresearchtool.

ThefirstbookonDEAwaspublishedin1988 (Wei,1998).DEAisalinearprogrammingtechnique whichmeasurestheefficiencyofmultipledecision makingunites(DMUs),whentheproductionprocess isastructureofmultipleinputsandmultipleoutputs. AssessingtheefficiencyofaDMUfromtheobserved dataisequivalenttoanalyzewhetherDMUison productionfrontierornot.PetersenandAndersen (1993)developedthesuper-efficiencyapproach,in whichtheefficientunitscanreceiveascoregreater thanone,throughtheunit'sexclusionfromthecolumn beingscoredinthelinearprogram.However,eachunit isevaluatedbyitsownweightasopposedtothecrossefficiencyconceptinwhichalltheunitsarecompared usingthesamesetsoftheweights.

DEAhasmanymerits,overseveralotherassessmentmethods.Assaidearlier,itwasanonparametricstatisticalevaluationmethod.Inadditionto DEAmodel,italsoprovidedwithusefulinsightsof managementinformationwitheconomicbackground, whichothermodelsdidnotprovide(Seiford,1996). Recently,DEAmodelhadbeensuccessfullyapplied inmanyotherresearchfields,likemanagement sciences,economics,andmilitaryaffairs.Apart fromthesesectors,DEAwasalsobeingregularly usedbypublicorganization,aswellasnonprofitorganizationi.e.hospitals(KuntzandVera,2007; VeraandKuntz,2007)orpublicadministrations departments,likepolice(Aristovniket al.,2013) toassesstheirefficiency.Recently,DEAhadalso beenusedintransportationforproductivityandpolicy andregulationsetting(Menachemet al.,2013). Recently,DEAtechniquehadbeenusedincaseof measuringoperationefficiencyofthebankingsectorin Serbia (Maletić et al.,2013).Alongwiththesesector researches,interonaltouristhotelindustrywasalsoa DEAmodelforidentifyingthecriticalinput-output combinationsfortheireachDMU(JieandLiang,2012).

Inthismanuscript,weappliedDEAmodelto analyzethecomparativeefficiencyofdifferentstructuraladjustmentschemesofagriculture,attheend,we chosethemostoptimalone.

Materials and Methods

Theoretical insight of DEA method

C2R (Charnes-Cooper & Rhodes) model and its definition

SeveralmodelsofDEAhadbeendevelopedbyseveral researchersafteritsinitialmodel,butstillC2Rwasthe firstandmostusedmodelpresentedbyCharnesand Cooper.Whichassumedthattherewerenorganization ordepartmentseachknownasseparatedecision makingunitsmentionedasDMU,eachofwhichhadm kindsofinputsandskindsofoutputs.Mathematically, respectivelymentionedastheinputandoutputvectors ofDMUjbyX=[xj1,xj2,…,x1(jm1)]T＞0andYj=(yj1, yj2,…,yjs).Whereas,xij(i=1,2,…,s)wastheith amountofoutputofDMUj,andyrj(r=1,2,…,s)was therthamountofoutputofDMUj.Thus,C2Rmodel forassessmentofDMUjwasasthefollowings:

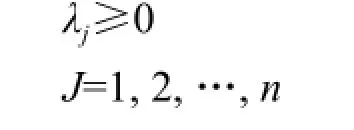
Fortheoptimalsolutionassumedthatoptimal solutionofthemodelwasθ0and,n.Now,if θ

0andsatisfied

Then,itmeantthatDMUj0representedaDEA efficientDMU.However,practicallyspeaking,applyingDEAC2RmodeltodetermineDEAefficiency usuallycounteredseveralhurdlesanddidcounter thoseissuesCharnesintroducedtheconceptofnon-ArchmediasvalueofDEAmodel.Therefore,new DEAmodelwithnon-Archmedianvalue"ε"was givenbelow:

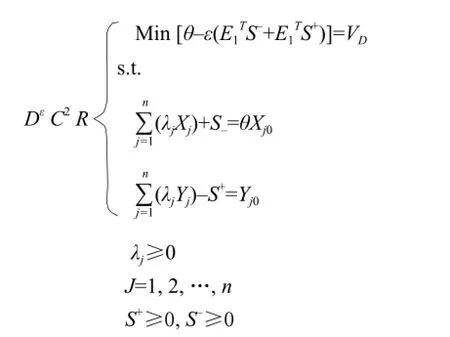
Whereas,E1=(1,1,…,1)T1×m,E=(1,1,…,1)T1×s. Theorem

SupposethattheoptimalsolutionsofmodelDεC2R wereλ0,S0–,S0+,andθ0.

1)Ifθ0=1andS0–=0,S0+=0,thenDMUj0wouldbe DEAefficient.

2)Ifθ0=1,thenDMUj0wouldbeweakDEA efficient.

3)Ifθ0＜1,thenDMUj0wouldbenotDEAefficient.

EconomicsimplicationofDEAefficient

Aspertheabovementionedtheorem,DMUsthat wereDEAefficientunderthemodelC2Rwereonthe productionfrontierofcorrespondingpossibilitiesset (Zhaoet al.,2002).Theyweretechnicalefficientas wellasscaleefficient,whichintermsmeantinthe productionpossibilityset,anditwasimpracticalto reduceanykindsofinputsbykeepinganykindsofoutputsassame,orincreasinganykindsofinputswith anykindsofoutputsremainingconstant.

DMUgotoptimaloutputswiththeprovidedinputs. Despitethefactthat,ifDMUunderthemodelC2R wasweakDEAefficient,weshouldbecertainwhether ornotitsslackvariableswereallequivalentto0.If S0–≠0, S0+=0,andthenitmeantthatundertheconstant outputsituation,fewbutnotallofitsinputscould shrink.Meanwhile,ifS0–≠0, S0+≠0, then this meant that fewoftheoutputscouldbetweakedpositively,while theinputsremainedunchanged.Evidently,DMU couldbemademuchbetterbyadjustingitsinputsor outputslogically.NotDEAefficientDMUwasnoton theproductionfrontier,itmustberemovedfromthe decisionmakingindexsetorifitcouldbeimproved, anditshouldbeuntilorunlessbecomingDEAefficientDMU.

Results

Multiple schemes assessment based on DEA method

Basedonthecharacteristicsofthedomesticstructure oftheagriculture,selecteddecisionmakingvariables forthemanuscriptwere:plantingacreageforcrops, fertilizerconsumption,andthetotalcostofproduction consideredasinputswhereastotalincome,total productionvalue,thetotalproductionofstockholdings, thetotalproductionofeconomiccrops,andthetotal productionofcornhadbeentakenasoutput.Inthe research,ontheagriculturalindustrialstructure ofPunjabProvince,Pakistan,amultipleobjective optimalprogrammingmodelwasdevised.Keeping multiplestrategiesinmind,weproposedfourschemes paralleltothemodel.Eachschemehadmultiplekinds ofinputsandoutputs.Itwascomplicatedtochoose theoptimaloneusingqualitativecomparisonorsome otherstraightforwardeasyquantitativeanalyses.In thismanuscript,weusedDεC2RmodelofDEAto assessthecomparativeefficiencyofmultipleschemes ofagriculturalindustrialstructure,attheendwechose themostfavorablealsoknownas"OPTIMAL"scheme toinstructandputintopractice.

i. Identifying DMUs

EachschemewasconsideredasaDMUj(whereas j=1,2,3,4).Theycontainedsimilarkindsofinputs andoutputs;additionallytheywereunderthesimilar productionconditions,whichsatisfiedalltheprerequisitesofDEAmethod.

ii. Opting input-output index of DMUs

Weoptedthreemaininputsandfiveoutputsindexes foreachDMUinviewofthatcorrespondingsolution oftheoptimalmodel,asshowninTable1.

iii. C2R model of DEA and its solution

WeestablishedDEA(DεC2R)modelsforeach DMUj(Whereasj=1,2,3,4).Respectivelytothe forecasteddatainTable1toevaluatethecomparative efficiencyofeachDMU.Then,thenon-Archmedias value"ε"takingthevalue10-6.UsingLINGOoptimal programmingsoftware,wecalculatedourmodels.The producesandcompiledsolutionsgeneratedbyLINGO areshowninTable2.

iv. Assessment and interpretation of analysis

ThesolutionsofDEA(DεC2R)modelshavebeen distributedintofourschemes(DMUs)intothreeranks: Rank1wasDEAefficientschemeDMU1andscheme DMU2.Bothofthemweretechnicallyandscale efficient.Whichillustratedthatproductionpossibility setofT1producedbyfourDMUs:

Therewasn'tasingleDMUwhichwasbetterthatof DMU1andDMU2.Illustratingmoreaccurately,itwas impossibleinT1toreduceinputsofDMUandDMU underthesituationofwithoutanyreductionsintheir outputs.

Rank2wasweakDEAefficientschemeDMU4. VerycomprehensivesolutionofDEAmethodassessingthecomparativeefficiencyofDMU4wasθ*=1 andAsper thetheorempresentedbefore,DMU4wasweakDEA efficient.Whichmeantthatinthepossibilitysetof T1,wecouldstillfindanewDMUj,whichwasmoreefficientthatDMU4.ItsinputsofX2andX3couldbe decreasedby19.57and31.286,respectively.Buton contrary,itsoutputsremaintunhandedasofDMU3.

Rank3wasDMU3.ItsefficiencywaslowerascomparedtoanyotherDMUj(j≠1). DEA solution model forthesameDMUwasshownbelow.

Itwasanindicationthatwecouldputupanew DMU3inthepossiblysetofT1usingalinearcombinationoffurtherDMUj.NowthisnewDMU3was DEAefficient,andthiskindofDMUwasknown asprojectionofDMU3intheproductionfrontier ofT1.

Table 1　Input and output of DMUj

Table 2　Assessment section of four DMUs (C²R)

MentioningDMU1by(X1,Y1)andtheprojection ofitwasmentionedusing(X1,Y1).Basedonthis, theprojectioncouldbecalculatedusingthesetwo formulas:

NotDEAefficientDMU'sprojectionshowedquite asignificantmeaningwiththebackgroundofeconomicsandmanagement.Itwasjustamanifestation ofhowtoimproveanotDEAefficientDMUtoan efficientDMU.Atthesametime,wecouldmake improvementsinthecorrespondingschemeonthe basisonsolutionofDEAmodel,andhence,weput upmoreandmoreefficientschemesforindustrial structureadjustment.

Conclusions

AftertheapplicationofDEA(DεC2R)model, weevaluatedtherelativeefficiencyofallthefour industrialproductionadjustmentstructureschemes ofPunjab(Pakistan)agricultureindustrialstructure.Theresultstakenbyandtheiranalysesshowedthat DEAmodelhadadistinctivevirtueincopingupwith evaluationandassessmentproblemswithmultiple inputsandclearlywithmultipleoutputs.Wecould notonlyevidentlyranktherelativesupremacyofthe fourschemes,moreover,gainsomereallyfunctional insightswithmanagementandeconomicsbackground (HuandHe,2000),whichelaboratedhowtodevelop andmodifynotDEAefficientschemesbyits projectionontheproductionfrontier.

TheproducedandcompiledsolutionsofDEA(DεC2R)modelgeneratedbyLINGOweresortedinto threeranks.Firstofthemincludedschemes1and4 exhibitedfewhelpfulguidelinesofPunjabProvince (Pakistan).Averygeneralcharacteristicofthesetwo schemeswasthatbothhighlightedswiftlydeveloping thestockbreeding,exertingthecomparativeadvantage ofagriculturalresourcesinPunjabProvince.Which alsoobeyedtherulesandprinciplesofagricultural industrialstructureadjustments.

References

AristovnikA,JankoSeljak,JernejMencinger.2013.Relativeefficiency ofpolicedirectoratesinSlovenia:anon-parametricanalysis. Expertsystemswithapplications. http://dx.doi.org/10.1016/ j.eswa.2012.08.027.

CharnesA,CooperWW.1978.Measuringtheefficiencyofdecision makingunits.European Journal of Operations Research,2:429.

HuYH,HeSH.2000.Methods of integrative assessment.Beijing, SciencePress.

JieW,LiangLA.2012.DEAmodelforidentifyingcriticalinput-output performancemeasures.Journal of Systems Science and Complexity,2: 14-21.

KuntzL,VeraA.2007.Modularorganizationandhospitalperformance. Health Services Management Research,20(1):48-58.

Maletic,Radojka,Kerca,et al.2013.ApplicationofDEAmethodology inmeasuringefficiencyinthebankingsector. Economics of Agriculture,Institute of Agricultural Economics,60(4):75-81.

MenachemBS,YishagY,BoazG,et al.2013.DEAworkshopon productivity,regulationandtransportation,Hebrewuniversity.http:// dea2013.huji.ac.il

PetersenP,AndersenNC.1993.Aprocedureforrankingefficientunitsin dataenvelopmentanalysis.Management Sciences,10:1261-1294.

SeifordLM.1996.Dataenvelopmentanalysis––theevaluationofstate oftheart.Journal of Production Analysis,7:99.

VeraA,KuntzL.2007.Process-basedorganizationdesignandhospital efficiency.Health Care Management Review,32(1):55-65.

WeiQL,1998.DEA method for relative efficiency evaluation-a new area in operations research.Beijing,RenminUniversityPress.

ZhaoX,XueJB,KeDY.2002.Ananalysisofcompetitiveness ofcommercialbankbasedonDEA.Journal of Quantitative and Technical Economics,9:84-87.

F304 Document code: A Article ID: 1006-8104(2015)-02-0087-05

16January2015

ZeeshanAhmad(1983-),researcher,Ph.D,engagedintheresearchofagriculturalproductionstructureadjustmentinPakistan.E-mail: zeeshanahmad00@yahoo.com

*.MengJun,professor,supervisorofPh.Dstudent,engagedintheresearchofagriculturalproductionstructureadjustment.E-mail: 1135044376@qq.com