基于Nuttall 窗-五点变换的改进FFT 介质损耗角测量算法
2015-11-25陈毅阳游胜强
金 涛 陈毅阳 游胜强
(福州大学电气工程与自动化学院 福州 350116)
0 引言
电力系统设备的重要组成部分之一就是电容型设备。若电容型设备发生设备故障,则在很大程度上能影响到电力系统的正常运行。而在所有的电容型设备故障中,很大一部分是由于绝缘问题引发的,所以有必要对其绝缘状态进行监测。其中,最关键的测试参量就是用于表征电容型设备绝缘状态的介质损耗角δ[1,2]。通过对电容型设备的介质损耗角δ的监测以及对其变化趋势的分析,能对电容型设备绝缘材料的性能、使用年限等进行有效的评估和预测[3,4]。
介质损耗角的测量方法主要可以分为硬件测量法和软件计算法。硬件法主要以过零检测为代表,通过硬件电路检测设备电信号的过零时刻,从而得到介质损耗角的值。软件法主要以谐波分析法为代表,通过对电压、电流信号进行处理而得到介质损耗角[5,6]。快速傅里叶变换(Fast Fourier Transform,FFT)具有处理速度快、不易受谐波干扰等特点,因此在软件法中常用FFT 来计算容性设备的介质损耗角。FFT 算法在同步采样下精度较好,但在非同步采样的情况下很容易由于频谱泄漏效应而产生计算误差[7,8]。为了减小非周期采样和数据截断所导致的频谱泄漏,采用Hanning 窗、Blackman 窗、Kaiser窗、三角自卷积窗等的加窗FFT 优化算法相继被提出,并在抑制频谱泄漏方面取得了较好的效果[9-11]。文献[12]提出了基于Hanning 自卷积窗的改进算法,该算法运算量小、易实现且计算精度高。文献[13]提出了基于Kaiser 窗的双谱线插值算法,得到了比汉宁窗更高的计算精度。文献[14]提出了将Blackman-Harris 窗与插值法相结合的改进的FFT 算法,有效地降低了介质损耗角的测量误差。文献[15]提出了莱夫-文森特窗函数三谱线插值算法及其修正公式,提高了FFT 算法的计算精度。如何同时在频域和时域进行改进而进一步提高介质损耗角的检测精度,是一个值得研究的问题。
为了进一步提高介质损耗角精度,本文对FFT在非周期采样和数据截断下的频谱泄漏现象进行分析,在加时域Nuttall 窗方法的基础上,对频域FFT输出序列进行五点加权变换进一步抑制频谱泄漏,从而提出基于Nuttall 窗-五点变换的改进FFT 算法。计算机仿真和实验结果表明,本文所提算法能有效消除谐波和直流分量的干扰,减少频谱泄漏效应并提高介质损耗角的测量精度。
1 介损测量算法及其误差来源分析
1.1 介质损耗角的定义
电介质实际等效原理图及其电压电流相量图如图1 所示,其中φ 为图中电介质等效RC 并联电路的功率因素角,φ 的余角δ 则为介质损耗角[16]。由图1 可得介质损耗角计算公式为


图1 电介质等效原理图与相量图Fig.1 The equivalent circuit and phasor of dielectric
式(1)为介损角的理论计算公式,实际上采用离散傅里叶变换(Discrete Fourier Transform,DFT)进行介损角的测量时,对流经电介质的电流和电介质两端的电压进行傅里叶分解,其表达式为

进一步分析可得介损角的测量值为

式中,δu、δi分别为电压、电流相角。
由上述对介损角的分析可知:介质损耗角与电压频率有关,二者之间呈反比例关系;电容性设备的电压、电流瞬时值,通过FFT 可以分离出电压、电流信号的基波及各次谐波幅值、频率、相位信息,从而可以较高精度地求得介质损耗角。
1.2 FFT 的频谱泄漏效应
理论上傅里叶变换是对无限长的时域信号进行变换,而工程实际上FFT 则是对有限长的时域信号进行变换,相当于对原来无限长的信号进行截断。截断后的信号相当于时域上在原无限长信号的基础上乘以一个矩形窗。由于时域上的乘积运算可以写成频域上的卷积运算,因此信号截断后会使得最后计算得到的信号频谱产生失真,最终得到的结果为矩形窗频谱和实际信号频谱的卷积而不是实际信号的真实频谱[17,18]。设电容性设备电压电流检测信号为

采样时所用长度为T 的矩形窗为

则其傅里叶变换的结果为
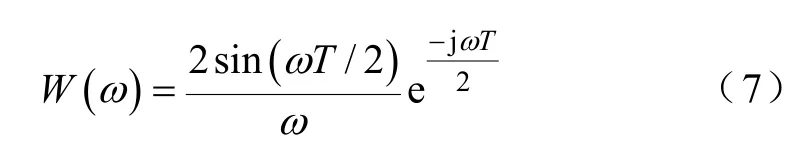
因此,在同步采样情况下,工程实际上通过快速傅里叶算法可以得到对应于分析频率 fAnl=mfs/N 的离散谱线图(其中m=0,···,N-1,fs为采样频率,N 为采样点数)。
令被测信号频率为 f=kfAnl,则可由FFT 算法得到频谱序列

但是由于电网频率是不断波动的,导致了实际在采用FFT 分析时很难满足同步采样的条件。假设 被 测 信 号 的 实 际 频 率 f '=(k+Δk )f,其 中0<Δk ≤1,则信号的频谱序列为

其中,当n=k 时


2 基于五点变换的改进FFT 相位分析方法
2.1 五点变换的FFT 算方法
由第1 节分析可知可计算FFT 输出序列 X(n)中第n 点的幅值为


为了增加第n 点主频点附近谱线的衰减速率,通过加权平均,便能得到新的傅里叶输出序列。采用式(12)对第n 条谱线及其附近5 个频点的谱线进行处理。

式中,n=1,2,…,N。特别地,把式(12)中不存在的项用 0 代替。此时,新的傅里叶序列输出频谱序列为


2.2 基于Nuttall 窗-五点变换的介损角分析法
为了减少应用FFT 对介质损耗角进行分析时频谱泄漏所带来的影响,本文在时域采用较小旁瓣峰值电平且具有较大旁瓣衰减速率的Nuttall 窗函数加窗的方式对信号进行截断[19,20]。式(14)为四阶Nuttall 窗的时域表达式。


图2 Nuttall 窗时域幅频特性Fig.2 The spectrum of Nuttall window in the time domain

图3 Nuttall 窗频域幅频特性Fig.3 The spectrum of Nuttall window in the frequency domain
图2 和图3 给出了Nuttall 窗的时域和频域下的幅频特性,可以看出Nuttall 窗具有良好的旁瓣性能。设频率为f=mfanl的电压和电流信号u(n)和i(n),以采样频率 fs对其离散化后得到的离散信号序列xi(n)和xu(n)为

式中, Inoise(n )、Unoise(n )为信号中的随机噪声;ki和ku为信号中的直流分量;H 为信号所含谐波分量个数、δhu和δhi为第h 次电压电流谐波信号的初相角、Uh和Ih为第h 次电压电流谐波信号的幅值。采用式(14)中的Nuttall 窗对电压电流信号进行加窗截断,可得输出序列Xi(n)和Xu(n)为

根据式(12)对Xi(n)和Xu(n)进行五点变换,最后得到FFT 输出序列Xi5(n)和Xu5(n),则容性设备的介质损耗角δ 可表示为

3 仿真分析
为了验证所提出的基于Nuttall 窗-五点变换介质损耗角的测量改进算法的有效性和精度,在多种干扰条件下对该改进算法进行了仿真研究。
绝缘介质的模型采用了电阻与电容并联模型,其电阻值为5kΩ,电容值为100μF,电压信号模型为

式中,A1为基波的幅值;A3为三次谐波的幅值;ω1为基波的角频率;θ1为基波的初相角;θ3为三次谐波的初相角;k 为直流分量的幅值;Random(t)为随机噪声函数;l 为随机噪声的幅值。
3.1 谐波的影响
在实际电力系统中,电信号通常会含有谐波成分,其中最常见并且幅值最大的是三次谐波。因此,选取三次谐波作为干扰进行介损角测量误差的研究。表1 为基波频率为50Hz、初相角为40°时的三次谐波干扰下介质损耗角测量的结果,其中 A3/A1表示三次谐波幅值与基波幅值之比。

表1 基波50Hz 时谐波对介质损耗角测量的影响Tab.1 Influence of harmonic component when the fundamental frequency is 50Hz
从表1 可以看出,在三次谐波干扰的情况下,Nuttall 窗-五点加权算法能有效抑制谐波对于介质损耗角测量结果的影响。因此,Nuttall 窗-五点加权改进算法在有谐波干扰的情况下仍然能进行介质损耗角的精确测量。
3.2 频率波动的影响
电网的频率实际上是缓慢动态变化的,其标准值为 50Hz。正常情况下,电力系统的频率允许±0.2Hz 的波动,对于容量较小的系统,频率波动范围可以允许到49.5~50.5Hz。
表2 为考虑电网频率波动的极限情况时采用本文算法所测得的介质损耗角。可以看出,本文的算法能有效消除频率波动导致的测量误差,测量结果绝对误差小于 0.5 ×10-6。

表2 频率波动对介质损耗角测量的影响Tab.2 Influence of frequency fluctuation on measurement of dielectric loss angle
3.3 采样点数的影响
固定采样频率为500Hz,采样点数从500 点取至600 点。表3 为当采样点数从500 增加至600 时所测得的介质损耗角。从表3 可以看出:随着采样点数的增加,介质损耗角的测量精度并没有显著提高,而且当采样点数不满足整周期采样时介质损耗角精度有所下降。因此,在满足整周期采样的情况下应尽可能减少采样点数以减小FFT 运行时间,以加快计算速度。

表3 采样点数对介质损耗角测量的影响Tab.3 Influence of changing the number of sampling points on measurement of dielectric loss angle
3.4 直流分量的影响
电力系统中,由于硬件电路的温度特性等原因,测得的电信号可能产生零点漂移现象,也就是在电信号中产生了直流分量。表4 为在不同直流分量值的影响下测得的介质损耗角,其中k/A1为直流分量与基波幅值之比。可以看出,随着直流分量的增大,测量结果依然保持相当高的精度,其相对误差小于5×10-6。

表4 直流分量对于介质损耗角测量的影响Tab.4 Influence of direct current component on measurement of dielectric loss angle
3.5 随机噪声的影响
随机噪声对于介质损耗角的影响见表5,其中l/A1表示随机噪声与基波幅值之比。可以看出,随机噪声与基波的幅值比在0.1~0.9 变化时,介质损耗角的测量结果精度仍然较高。

表5 随机噪声对介质损耗角测量的影响Tab.5 Influence of random noise on measurement of dielectric loss angle
4 实验验证与分析
为了验证所提出的理论和算法,本文在实验室搭建硬件实验电路进行了相关实验。在实际的容性设备电器工作的过程中,由于开关操作等原因会产生10MHz 左右的高频干扰,这些高频噪声干扰会降低测量结果的精确度,因此,必须采用低通滤波器对信号中的高频干扰进行抑制。根据工程实际经验,低通滤波器的截止频率通常选择为基波频率的 10倍。由于实际监测介质损耗角时更加关注的是多路信号之间的相位差的稳定性,本文采用滤波器的传递函数为


图4 设计的低通滤波器幅频特性Fig.4 Amplitude-frequency characteristic diagram of designed low pass filter
通过设计如图5 所示的传感器电路、信号调理电路利用标准容性设备进行检测,并通过数据采集卡PCIE1816H 把采集的信号传递到上位机,分别采用传统FFT 算法及本文所提算法进行介质损耗角的求解,然后改变信号的频率、噪声幅值、直流分量幅值以及采样点数后采集电压和电流信号数据,来验证本文所提方法的先进性。

图5 实验用硬件电路Fig.5 Hardware diagram of experiments
4.1 频率变化时的实验结果
为了验证本文提出的基于Nuttall 窗-五点变换FFT 的介质损耗因数算法在被测信号基波频率波动情况下的计算精度的有效性,将信号源中电压基波频率分别设定为49.5、49.7、50、50.2、50.5Hz,在其余参数不变的情况下通过介质损耗因数监测平台进行介质损耗因数的测量并与基于传统FFT 的介质损耗因数算法进行比较,实验分析结果如图6 所示。

图6 基波频率变化时不同算法相对误差对比Fig.6 Relative error comparison of different algorithms when the fundamental frequency changed
从图6 可以看出:在基波频率50Hz 附件时,两种算法的介质损耗角分析精度基本相同,但在基波频率偏移工频50Hz 的情况下,基于Nuttall 窗-五点变换FFT 的介质损耗因数算法的计算精度要高于传统FFT 算法;并且相对于传统FFT,随着基波频率与50Hz 之间偏移量的增加,本文所提算法的计算误差波动要远小于传统FFT 算法的计算分析结果,这说明本文算法能更好地抑制频率波动带来的计算误差。
4.2 噪声幅值变化时的实验结果
为了验证基于Nuttall 窗-五点变换FFT 的介质损耗因数算法在被测信号含有噪声情况下的计算精度的有效性,将信号源产生的电压信号的噪声幅值从0 增加至1(pu),其中步长为0.1(pu),在其余参数不变的情况下通过介质损耗因数监测平台进行介质损耗角的计算并与基于传统FFT 的介质损耗角算法进行比较,实验分析结果如图7 所示。

图7 噪声幅值变化时不同算法相对误差对比Fig.7 Relative error comparison of different algorithms when the noise component changed
从图7 可以看出:随着噪声的增加,基于Nuttall窗-五点变换 FFT 的介质损耗角计算方法和传统FFT 方法的计算精度都在降低,但基于Nuttall 窗-五点变换FFT 的介质损耗因数算法的计算精度仍高于传统FFT 算法,这说明本文提出的方法优于传统方法。
4.3 直流分量变化时的实验结果
为了验证基于Nuttall 窗-五点变换FFT 的介质损耗因数算法在被测信号含有直流分量情况下的计算精度的有效性,将信号源产生的电压信号的直流分量(相对基波幅值)从0 增加至1(pu)(步长为0.1(pu)),在其余参数不变的情况下通过介质损耗因数监测平台进行介质损耗因数的计算并与基于传统FFT 的介损因数算法进行比较,实验结果如图8所示。

图8 直流分量变化时不同算法相对误差对比Fig.8 Relative error comparison of different algorithms when the DC component changed
从图8 可以看出:随着直流分量幅值增加,直流分量变化时对传统FFT 以及基于Nuttall 窗-五点变换FFT 的介质损耗因数算法的影响都较小,且本文提出的介质损耗角测量方法具有较好的效果。
4.4 采样点变化时的实验结果
为了验证基于Nuttall 窗-五点变换FFT 的介质损耗因数算法在采样点数改变情况下的计算精度的有效性,将采样点数从1 200 点增加至3 000 点,在其余参数不变的情况下通过介质损耗因数监测平台进行介质损耗因数的计算并与基于传统FFT 的介质损耗因数算法进行比较,实验结果如图9 所示。

图9 采样点数变化时不同算法相对误差对比Fig.9 Relative error comparison of different algorithms when the number of sampling points changed
从图9 可以看出:在窗长为非整周期的情况下,基于Nuttall 窗-五点变换FFT 的介质损耗因数算法和传统FFT 算法的计算误差都有所增加,但是前者误差波动较小。因此可以得出结论:基于 Nuttall窗-五点变换FFT 的介质损耗因数算法对于非整周期采样下的误差抑制能力更好。
5 结论
采用传统FFT 进行介质损耗因数的计算时,由于无法满足整周期采样会使得计算结果误差较大。为了减小非整周期采样带来的误差,本文提出了基于Nuttall 窗的改进五点变换FFT 算法,并通过计算机仿真及实验验证了上述算法的精度和有效性。本文提出的方法能有效降低非整周期采样带来的误差,并且在频率波动、直流分量变化、采样点数变化等条件下仍能保持相当高的介质损耗因数计算精度。
[1]段大鹏,江秀臣,孙才新,等.基于正交分解的介质损耗因数数字测量算法[J].中国电机工程学报,2008,28(7):127-133.Duan Dapeng,Jiang Xiuchen,Sun Caixin,et al.A novel algorithm of dielectric loss measurement based on orthogonal decomposition[J].Proceedings of the CSEE,2008,28(7):127-133.
[2]徐志钮,赵丽娟,律方成,等.傅里叶算法测量介质损耗的误差分析与应用[J].电网技术,2011,35(12):124-129.Xu Zhiniu,Zhao Lijuan,Lü Fangcheng,et al.Error analysis on dielectric loss measurement by Fourier algorithm and its application[J].Power System Technology,2011,35(12):124-129.
[3]孙鹏,杨永越.五点加权FFT 介质损耗角测量算法的研究[J].高压电器,2015,51(3):88-92.Sun Peng,Yang Yongyue.Five-point weighted FFT algorithm for measurement of dielectric loss angle[J].High Voltage Apparatus,2015,51(3):88-92.
[4]董爽,李天云,王永,等.在线检测介质损耗角的矩阵束方法[J].电工技术学报,2015,30(18):229-236.Dong Shuang,Li Tianyun,Wang Yong,et al.An on-line detection method of dielectric loss angle based on matrix pencil algorithm[J].Transactions of China Electrotechnical Society,2015,30(18):229-236.
[5]张红瑛,滕召胜,温和,等.九点变换改进FFT 高精度谐波分析方法[J].电力系统及其自动化学报
,2010,22(6):38-43.Zhang Hongying,Teng Zhaosheng,Wen He,et al.Nine points’ polynomial transform improved FFT for high precise harmonic analysis[J].Proceedings of the CSU-EPSA,2010,22(6):38-43.
[6]高云鹏,滕召胜,曾博,等.基于 Kaiser 窗频谱校正的介质损耗因数测量[J].电工技术学报,2009,24(5):203-208.Gao Yunpeng,Teng Zhaosheng,Zeng Bo,et al.Dielectric loss factor measurement based on Kaiser window spectral correction[J].Transactions of China Electrotechnical Society,2009,24(5):203-208.
[7]高云鹏,李峰,陈婧,等.基于Teager-Kaiser 能量算子 Rife-Vincent 窗频谱校正的电压闪变测量[J].电工技术学报,2014,29(6):248-256.Gao Yunpeng,Li Feng,Chen Jing,et al.Voltage flicker measurement using the Teager-Kaiser energy operator based on Rife-Vincent window spectral correction[J].Transactions of China Electrotechnical Society,2014,29(6):248-256.
[8]高云鹏,滕召胜,温和,等.基于 Kaiser 窗的相位差校正及tanδ 测量应用[J].湖南大学学报:自然科学版,2009,36(4):48-52.Gao Yunpeng,Teng Zhaosheng,Wen He,et al.Dielectric loss factor measurement based on Kaiser window phase difference correction[J].Journal of Hunan University:Natural Sciences,2009,36(4):48-52.
[9]王刘旺,黄建才,孙建新,等.基于加汉宁窗的FFT 高精度谐波检测改进算法[J].电力系统保护与控制,2012,40(24):28-33.Wang Liuwang,Huang Jiancai,Sun Jianxin,et al.An improved precise algorithm for harmonic analysis based on Hanning-windowed FFT[J].Power System Protection and Control,2012,40(24):28-33.
[10]唐轶,陈奎,韩智强,等.布莱克曼函数频域插值电力谐波计算[J].电力系统及其自动化学报,2013,25(3):142-146.Tang Yi,Chen Kui,Han Zhiqiang,et al.New calculation method of electric power harmonic in frequency domain interpolation of Blackman windows[J].Proceedings of the CSU-EPSA,2013,25(3):142-146.
[11]温和,滕召胜,曾博,等.基于三角自卷积窗的介损角测量算法及应用[J].电工技术学报,2010,25(7):192-198.Wen He,Teng Zhaosheng,Zeng Bo,et al.Dielectric loss angle measurement algorithm and application based on Triangular self-convolution window[J].Transactions of China Electrotechnical Society,2010,25(7):192-198.
[12]孙鹏,杨永越,刘黎明,等.基于 Hanning 卷积窗的DFT 介质损耗角测量算法[J].电测与仪表,2014,51(16):73-77.Sun Peng,Yang Yongyue,Liu Liming,et al.A DFT dielectric loss angle measurement algorithm based on Hanning convolution window[J].Electrical Measurement &Instrumentation,2014,51(16):73-77.
[13]高云鹏,滕召胜,卿柏元.基于Kaiser 窗双谱线插值 FFT 的谐波分析方法[J].仪器仪表学报,2010,31(2):287-292.Gao Yunpeng,Teng Zhaosheng,Qing Baiyuan.Harmonic analysis based on Kaiser window double spectrum line interpolation FFT[J].Chinese Journal of Scientific Instrument,2010,31(2):287-292.
[14]徐志钮,律方成,李和明.加Blackman-Harris 窗插值算法仿真介损角测量[J].高电压技术,2007,33(3):104-108.Xu Zhiniu,Lu Fangcheng,Li Heming.Simulation analysis of dielectric loss angle measured by the Blackman-Harris[J].High Voltage Engineering,2007,33(3):104-108.
[15]黄冬梅,龚仁喜,焦凤昌,等.菜夫-文森特窗三谱线插值的电力谐波分析[J].电力系统保护与控制,2014,42(2):27-34.Huang Dongmei,Gong Renxi,Jiao Fengchang,et al.Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation[J].Power System Protection and Control,2014,42(2):27-34.
[16]温和,滕召胜,王永,等.频谱泄漏抑制与改进介损角测量算法研究[J].仪器仪表学报,2011,32(9):2087-2094.Wen He,Teng Zhaosheng,Wang Yong,et al.Study on spectral 1eakage suppression and improved dielectric loss angle measurement method[J].Chinese Journal of Scientific Instrument,2011,32(9):2087-2094.
[17]郝西伟,杨大伟,刘广艳,等.高精度FFT 算法在介损监测中的理论与仿真研究[J].高压电器,2009,45(2):57-61.Hao Xiwei,Yang Dawei,Liu Guangyan,et al.Theoretical and simulation study on high accuracy FFT algorithm for tanδ monitoring[J].High Voltage Apparatus,2009,45(2):57-61.
[18]温和,滕召胜,王一,等.基于三角自卷积窗的介损角高精度测量算法[J].电工技术学报,2009,24(3):203-208.Wen He,Teng Zhaosheng,Wang Yi,et al.High accuracy dielectric loss angle measurement algorithm based on triangular self-convolution window[J].Transactions of China Electrotechnical Society,2009,24(3):203-208.
[19]许珉,杨阳,陈飞,等.基于 Nuttall(Ⅰ)窗的插值FFT 算法[J].电力系统保护与控制,2011,39(23):44-48.Xu Min,Yang Yang,Chen Fei,et al.An interpolated FFT algorithm based on the Nuttall(I) window[J].Power System Protection and Control,2011,39(23):44-48.
[20]曾博,唐求,卿柏元,等.基于Nuttall 自卷积窗的改进 FFT 谱分析方法[J].电工技术学报,2014,29(7):59-65.Zeng Bo,Tang Qiu,Qing Baiyuan,et al.Spectral analysis method based on improved FFT by Nuttall self-convolution window[J].Transactions of China Electrotechnical Society,2014,29(7):59-65.
