新型外转子低速直驱永磁游标电机的损耗

朱 洒 程 明 李祥林 李 顺

（东南大学电气工程学院 南京 210096）

1 引言

基于磁齿轮原理的永磁游标电机具有低速大转矩的特点，在诸如风力发电、电动汽车等低速直驱领域有良好的应用前景，正引起越来越多研究人员的重视[1-3]。在直驱风力发电中，由于风机转速较低，设计的传统永磁同步电机的尺寸通常较大[4,5]。文献[2]中提出了一种永磁游标电机，利用磁齿轮的场调制原理，将转速较低的转子永磁磁场调制成转速较高的定子气隙磁场，即实现了所谓的“自增速”效果，这样，定子绕组可按高速旋转磁场来设计，有利于提高电机的功率密度。文献[6,7]在比较几种磁齿轮电机的基础上提出了一种具有更高转矩密度的新型永磁游标电机，如图1 所示。该电机为外转子结构，采用铝壳固定，外转子的聚磁结构有效地增加了转矩密度。

尽管该类型电机具有转矩密度高，省去齿轮箱等诸多优点，但其定子齿槽同时起调磁块的作用，为开槽结构，会产生高次空间谐波，这有可能引起较大铁耗并在永磁体和外面铝壳中感应出较大的涡流损耗。另外，由于绕组位于电机内部，且电机功率密度较高，有必要对其损耗和温升特性进行分析研究，以保证电机的安全可靠运行。

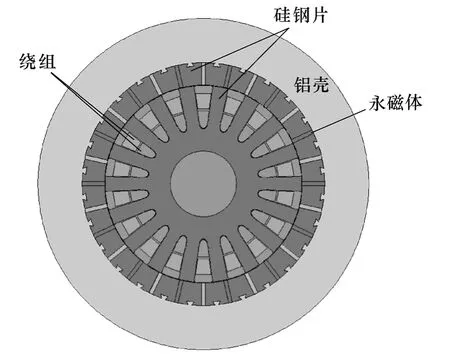
图1 游标电机剖面图Fig.1 Cross section of the vernier machine

本文首先针对样机的空载损耗进行计算，并进行了实验验证。然后计算了负载电流对损耗的影响，并针对永磁材料特性对温度敏感的特点，分析了温度变化对电机损耗和性能的影响。针对铝壳中的涡流损耗，提出了降低损耗的措施。

2 空载损耗分析与实验验证

电机空载损耗包括铁耗Piron，永磁体内部涡流损耗PePM，铝壳内部涡流损耗PeAL和机械损耗Pm。由于电机转速较低，可忽略外转子与空气间的风磨损耗。下面以一台5.5kW 的样机为例，对该电机的空载损耗进行计算。样机的参数见表1。

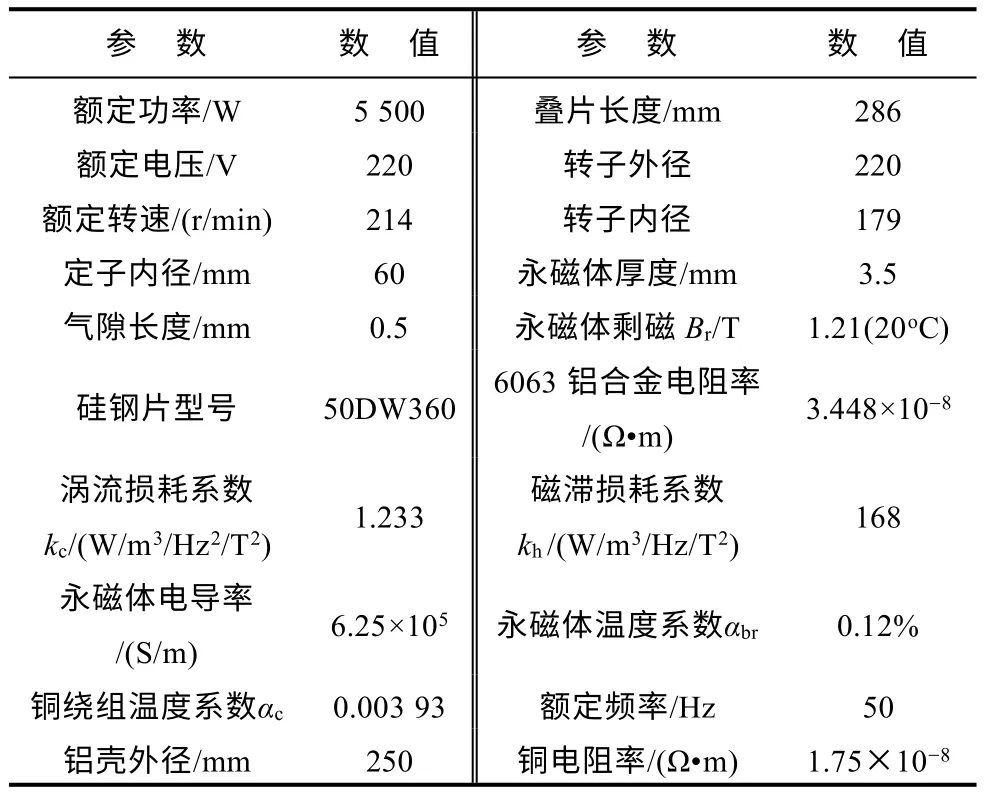
表1 样机参数Tab.1 Specification of prototype

2.1 铁耗计算

铁耗计算采用二维时步有限元法得到每个网格磁通密度的变化情况，将每个网格计算损耗在一个周期内取平均然后求和即为总的铁耗。其中每个网格瞬时损耗计算公式为

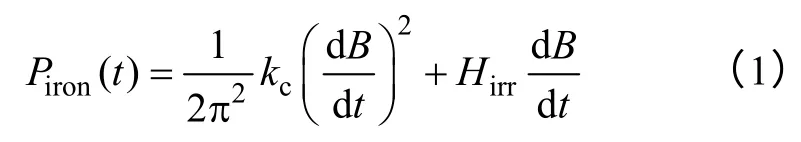
式中 B——每个网格的磁通密度，对于二维磁场，其包含两个分量；

kc——涡流损耗系数；

Hirr——每个网格的磁场强度中的不可逆分量，其详细计算过程可参考文献[8]。

2.2 永磁体内部涡流损耗计算

由于电机采用了磁齿轮增速原理，内定子槽口很大，这导致电机旋转时，永磁体产生的磁通所经过的磁阻会有较大变化，导致永磁体内部磁通密度产生较大变化，且交变频率较高，会在永磁体内感应出较大涡流损耗。同理，永磁体的漏磁通也会在铝壳中感应出涡流损耗。图2 给出了采用有限元法计算磁通密度变化点的位置，A 点反映永磁体内部磁通密度的变化，而B 点反映铝壳中永磁体漏磁磁通密度的变化。图3 中给出了当电机以额定转速214r/min 旋转时，对应点切向磁通密度的变化，此时磁通密度变化的频率为64.2Hz。

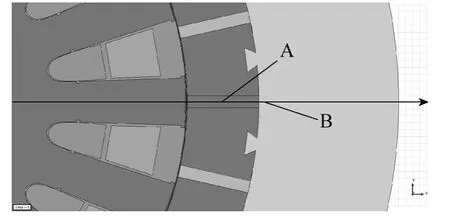
图2 计算磁通密度点位置Fig.2 Positions for calculation of flux density

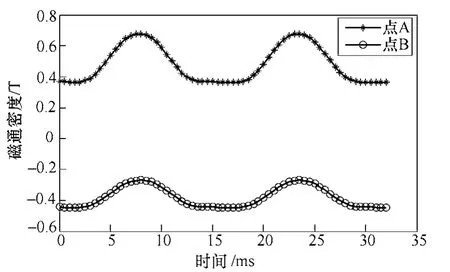
图3 磁通密度分切向分量变化图Fig.3 Variation of the tangential components of flux density

由于二维有限元法中电流只有垂直于电机平面的分量，理论上讲要准确计算永磁体中的涡流损耗需要进行三维有限元计算[9,10]，但耗费时间较长并需要较大内存，尤其在重复计算电机不同工况下的损耗时更是如此。在文献[11]中通过将每块永磁体等效成整块导体，并通过将其与大电阻的串联来约束面电流使其满足

式中 It——单块永磁体截面上的总电流；

St——该块永磁体的截面积；

J——总的电流密度。

空载时包含导体块和永磁体在内的二维有限元瞬态场计算的控制方程为[12]

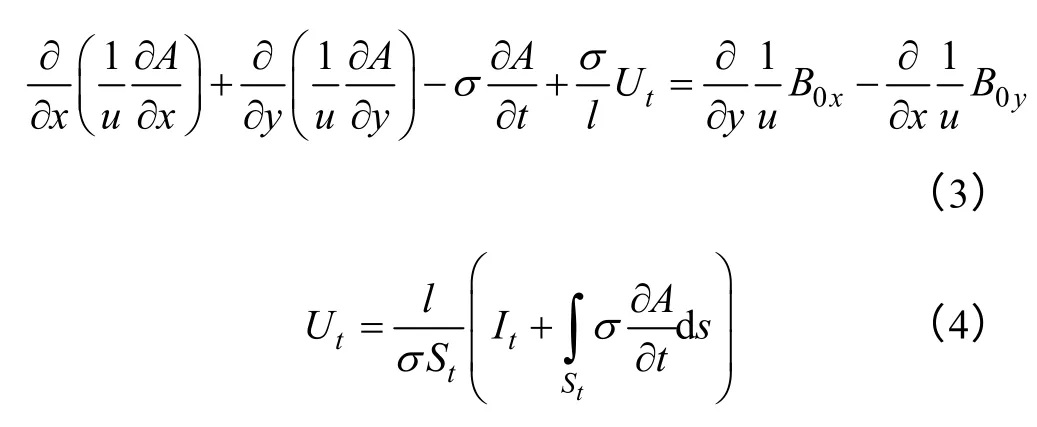
式中 A——磁位；

u——磁导率；

σ——导体块电阻；

l——轴向长度；

Ut——各块导体的端电压；

B0x和B0y——x 和y 方向上的剩磁，对于其他区域这两个值为0。

在利用二维瞬态有限元计算时，若不考虑外电路的耦合，在常用的有限元软件如Ansoft Maxwell中默认地将Ut设为0，这就意味着导体无限长或者说每块导体两端短路，每个网格的感应电流等于-σ ·∂ A /∂t，此时并不能保证导体截面上的总电流为0。然而，永磁体中的涡流只在内部循环，可以想象在每块永磁体的轴截面上都应该满足总电流等于0的条件，即流进等于流出。所以通过在每个导体块上施加It=0 的条件或者利用场路耦合有限元法将每个导体快与一个大电阻相连来近似实现总电流为0，都可以近似模拟永磁体中涡流的情况，实现较准确、高效的永磁体涡流损耗计算。

为了检验二维有限元法计算涡流损耗的有效性，将二维计算的结果与三维涡流损耗的计算结果进行了比较。对于图1 所示样机，至少取1/2 电机区域进行计算，在三维模型中需要较大内存空间和很长计算时间。为节省计算时间，将内定子的齿数设为14，这样就可以取模型的1/14 区域进行计算，如图4 所示。此外，计算中未考虑铝壳的影响。

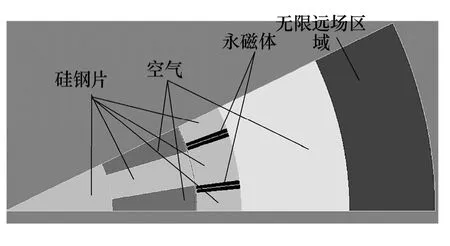
图4 计算区域示意图Fig.4 Calculation region

图5 所示为三维有限元法得到的某时刻永磁体内涡流损耗分布。可以看出，由于永磁体内部磁通密度主要是切向分量在变化，感应出的涡流与这种变化一致。不少文献中指出采用轴向或径向分段的方式可以减小永磁体涡流损耗，这主要是因为增加了涡流回路中的电阻，在分段长度小于趋肤深度时更加明显。需要指出的是，图5 中给出的是永磁体轴向一半的情况。左图为永磁体不分段的情况，右图为永磁体轴向分4 段的情况。

图5 某时刻永磁内部涡流密度分布Fig.5 Eddy current density inside PM

图6 所示为采用约束了每块永磁体截面上总电流为0 的二维有限元法计算得到的永磁体内部涡流损耗和采用三维有限元法计算的结果对比。可以看出，二维有限元计算结果与三维计算结果在变化趋势上一致，但二维计算结果偏高。这主要是由于二维有限元法无法考虑到端部漏磁以及端部的电阻和涡流。

图6 永磁体内瞬时涡流损耗Fig.6 Eddy current loss inside PMs

可以考虑采用分段的方式减小永磁体内部涡流损耗，但这会增加加工的难度。而且在下面的计算中发现由于样机转速较低，永磁体涡流损耗在总损耗中占的比重不高，所以轴向分段并非十分必要的。

2.3 铝壳内涡流损耗

起固定外转子作用的铝壳，其内部感应出的涡流损耗同样不可忽略[13]。从图3 可以看出，B 点交变磁通密度峰峰值约为0.2T，频率为64.2Hz。由于铝合金具有较高的导电率，因此会在铝壳中感应出较大涡流损耗。采用和永磁体内涡流损耗相同的二维有限元法进行计算，可以得到电机额定转速空载运行时某一时刻铝壳中瞬时损耗密度的分布如图7a 所示，可以发现在靠近永磁体的位置由于漏磁磁通密度较大，其涡流损耗也较大。因此，可以采用在此处挖一个半径约为6.7mm 的半圆孔的方法来减小涡流损耗。经计算发现，空载运行时图7b 的涡流损耗比图6a 减小了35%。

图7 某时刻铝壳内涡流损耗分布Fig.7 Eddy current loss in aluminum case

另外可以想象，如果铝壳电导率为0 或无穷大时铝壳内的涡流损耗都应该为0，所以铝壳内部的涡流损耗随铝壳电导率不是单调的函数关系，为此经过计算给出了额定转速空载运行时，铝壳涡流损耗随电导率变化关系如图8 所示。

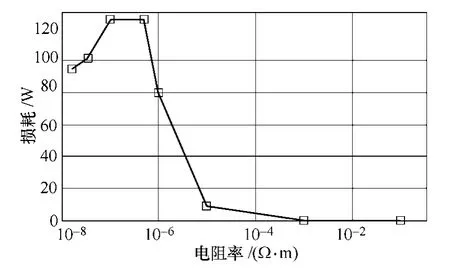
图8 铝壳内涡流损耗随铝壳电阻率变化图Fig.8 Eddy current loss versus resistivity in aluminum case

在保证安装机械强度的情况下，还可以考虑减小铝壳的厚度。减小铝壳厚度一方面减小了漏磁通感应的面积，但另一方增大涡流流通的电阻，其随厚度的变化也不是单调的。通过计算得到铝壳内涡流损耗随厚度变化如图9 所示。可以看出当铝壳厚度从40mm 减小到20mm 时铝壳的涡流损耗只是略有下降，但当铝壳厚度继续减小时铝壳内涡流损耗反而迅速增加。这是由于涡流源主要集中在紧靠永磁体处，如图7a 所示，减小了外层的铝壳厚度并不影响这部分主要的涡流源。另外，涡流会在铝壳内循环，减小厚度相当于增大了涡流流通的电阻，从图8中可以看出，从当前铝壳的电阻率3.448×10-8Ω·m开始增大电阻率，涡流损耗反而会增加，这就解释了为什么减小铝壳厚度反而增大了涡流损耗。

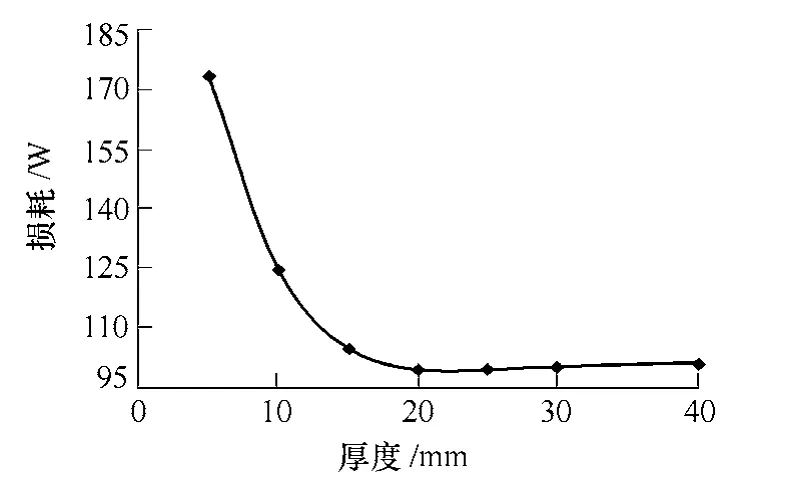
图9 铝壳涡流损耗随厚度变化关系Fig.9 Eddy-current loss versus case thickness

2.4 各种电磁损耗对比

图10 所示为不同电磁损耗随转速变化的关系图。可以看出硅钢片的涡流损耗和永磁体内的涡流损耗正比于转速的平方，磁滞损耗正比于转速，而铝壳内的涡流损耗近似与转速成正比。同样是涡流损耗，却出现了不一样的变化趋势。在文献[14,15]中指出涡流损耗分为电阻阻滞型和电感阻滞型，它并不总是随着频率的增加而以平方倍的关系增加。这主要取决于与导体本身尺寸和趋肤深度的关系，从另一角度讲就是涡流本身能否对磁场产生较大影响。在永磁体中，由于永磁体电阻率较大，而且永磁体本身就是场源，感应的涡流并不能对永磁体内的磁场产生较大影响。因此，永磁体内涡流随转速线性增加，就导致损耗以平方关系增加。在铝壳中的涡流损耗主要是变化的漏磁通产生的，而铝壳的电阻率较小，可以感应出有效的涡流来阻滞漏磁通的变化，因此涡流并不是随着转速线性增加，涡流损耗也就不是随转速以平方倍的关系增加。可以想象，如果铝壳是一个超导体，它具有保存其匝连磁链不变的特性，当转速升高时，如果漏磁通的幅值不变，那么铝壳内感应的涡流的频率将增加而幅值不变。也就是说在这种极端情况下，涡流的大小不随转速而变化。

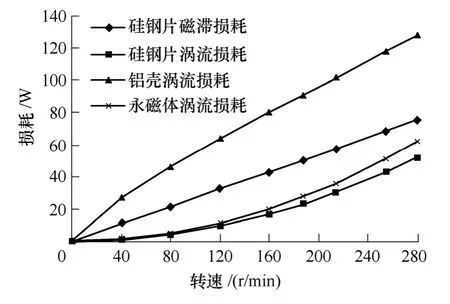
图10 不同成分的电磁损耗随转速变化关系Fig.10 Magnetic losses in different parts versus speed

另外可以看出铝壳内的涡流损耗占了电磁损耗中相当大的比重，减小该损耗，可以明显提高电机效率，因此，可以考虑采用其他不导电材料如高强度塑料等避免涡流损耗。

2.5 机械损耗计算与实验验证

轴承的摩擦损耗与轴承的品质、润滑和安装等多种因素有关系。由于电机为外传子结构，轴承的安装结构不同于传统电机结构，参照文献[16,17]中的方法,机械损耗采用下式估算为

式中 Pfr——轴承的摩擦损耗；

Pwind——风摩损耗，由于电机转速较低，计算发现Pwind可以忽略不计；

Grotor——转子的质量；

nr——轴承个数，该值为4；

N——转速（r/min）；

Dout——外转子直径；

L——外转子长度。

图11 给出了该电机的铁磁损耗和机械损耗以及空载总损耗随转速的变化曲线。

为检验分析计算的正确性，对实验样机进行了空载试验，由一感应电机拖动被试电机作空载运行，采用HBM 转矩转速传感器测量被试电机的输入转矩和转速，得到空载总损耗，如图11 中所示。对比空载总损耗的计算值和实测值可见，二者基本一致，从而说明本文的铁磁损耗和机械损耗计算方法是正确可行的。

图11 计算损耗与实验验证Fig.11 Comparison between calculated and measured losses

3 负载特性对损耗的影响

负载时电枢电流产生的磁场会影响电机中的磁通密度分布，进而影响损耗。本节采用与上节相同的损耗计算方法，分析负载电流对电机损耗的影响。根据电机设计参数，可得电机的额定电流为8.33A。额定转速不同功率因数下，发电运行时负载电流对损耗的影响见表2。可以看出不同的发电状态对电机输出端电压、输出功率和损耗均有较大影响。当输出电流与q 轴夹角为0°时，此时电枢电流产生磁动势和永磁体产生磁动势垂直。合成磁场略有增加，此时输出转矩最大。当负载电流滞后于q 轴，电流起增磁作用，此时电机吸收无功，电机输出电压升高，铁耗也增大。当输出电流超前于q 轴时，电枢电流起去磁作用，电机损耗下降，这种影响对于铝壳中的涡流损耗体现的最为明显，而这部分损耗所占比重又较大，因此需要考虑电机的不同工况对损耗的影响。

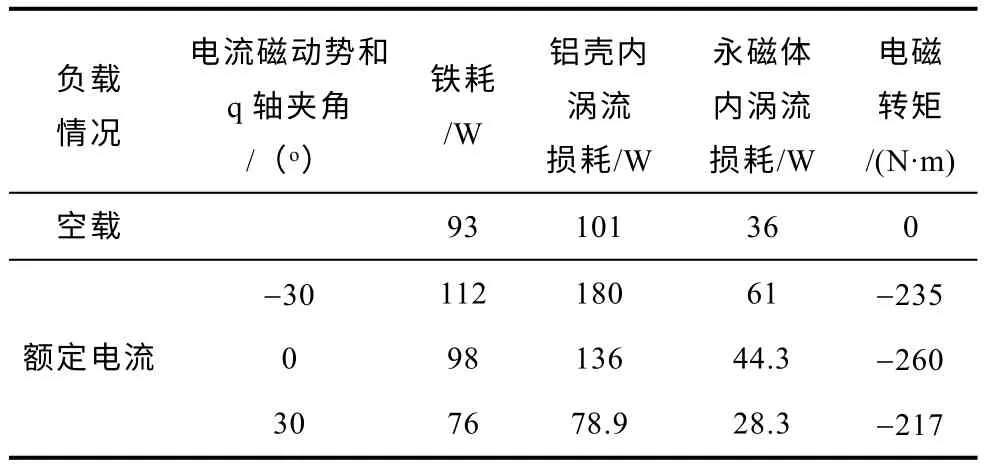
表2 负载电流对电磁损耗影响Tab.2 Influence of load current on loss

另外，负载电流也会在绕组中产生铜耗，该部分损耗计算公式为

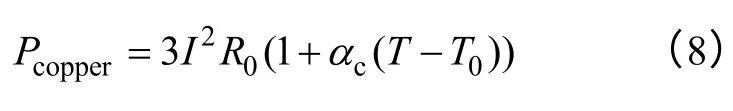
式中 R0——绕组温度为T0时的电阻值；

I——相电流有效值。

4 温升对电磁损耗的影响

由于钕铁硼永磁材料的特性对温度较为敏感，在永磁电机设计中必须考虑温度对电机性能的影响，而损耗也不例外。永磁体剩磁随温度变化关系为

式中 Br0——温度为T0时永磁体的剩磁；

Br——温度为T 时永磁体的剩磁。

为简化分析，只考虑永磁体剩磁随温度的变化，认为相对磁导率不变且退磁曲线始终是一条直线。采用不同温度下的永磁体剩磁进行计算，得到几个不同温度点下额定负载且电流磁动势与q 轴夹角为0 时各部分电磁损耗如图12 所示。可以看出各部分损耗的变化都可以用一个线性函数近似表示。经过计算发现，当只考虑永磁体温升影响时，永磁体温度从20℃升至120℃时，永磁体剩磁下降了12%，而输出转矩下降了10%，铁耗下降了9%，永磁体涡流损耗下降了15%，铝壳涡流损耗下降了17%，总的电磁损耗下降了14%。可以看出，各部分损耗随温度变化都较平坦，在工程计算中通常可以预设一个永磁体大约的工作温度，然后再进行计算，如上文的空载损耗计算就是预设永磁体温度为40℃情况下完成的。若需要较高准确度则需要结合温度场分析通过迭代的方式进行。

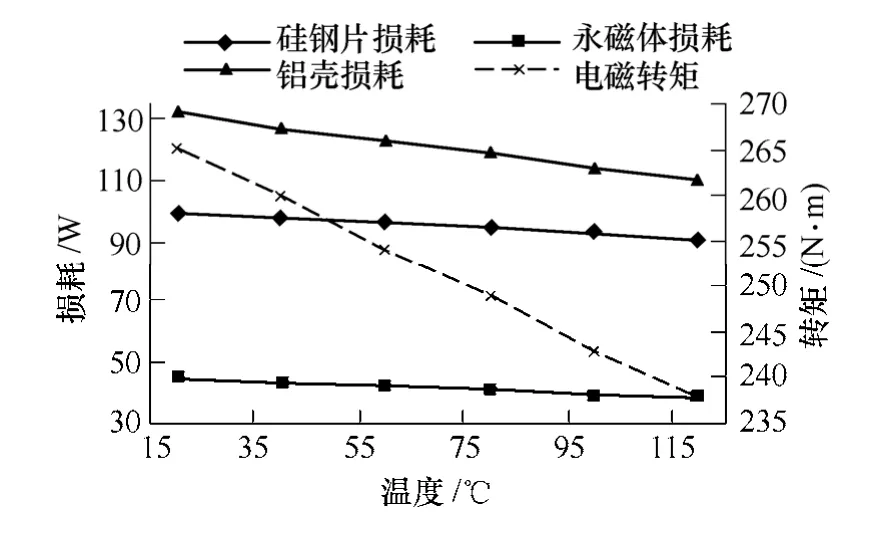
图12 永磁体温度对电磁损耗的影响Fig.12 Influence of magnet temperature on loss

在上面的计算中仅考虑了永磁体温度对各部分损耗的影响，然而在实际电机工作中，永磁体的温升并不是孤立的，当永磁体温度升高的同时，铝壳也必然存在温升，而铝的温度系数为0.004 29，略高于铜。而在图8 中经过计算发现铝壳电阻的增加会引起损耗的增加，而且铝壳涡流损耗在电磁损耗中占有较大比重。因此，进一步分析了同时考虑永磁体温升和铝壳温升时铝壳涡流损耗的变化情况。由于永磁体、外转子硅钢片和铝壳紧密连接且导热率都较大，它们的温差较小，因此在计算中近似认为铝壳和永磁体有着相同的温度。经过计算发现，当永磁体和铝壳的温度从20℃升高到120℃时，铝壳涡流损耗下降了11%，而不是只考虑永磁温升时的17%。

总而言之，电机的温升会影响电机的各种性能，而且耦合关系比较复杂。但从图12 中可以看出这种影响不是非常大，而且变化趋势比较平坦。在工程分析中需要根据实际情况抓住主要因素进行分析，最终目的是既能满足工程计算的需要又能节约计算时间和成本。

5 结论

本文采用二维场路耦合有限元法对一种新型外转子永磁游标电机的损耗特性进行了分析计算。针对永磁体内部涡流损耗，给出了二维有限元法计算的要点，并与三维有限元法的计算结果进行了对比。针对电机铝壳内的涡流损耗，分析了影响损耗的因素，并提出了减小损耗的方法。样机实验结果验证了计算方法的正确性。在此基础上，进一步研究了不同负载情况下的损耗特性，并探讨了温度变化对电磁转矩和损耗特性的影响。

[1]Toba Akio,Lipo T A.Generic torque-maximizing design methodology of surface permanent-magnet vernier machine[J].IEEE Transactions on Industry Applications,2000,36(6):1539-1545.

[2]Li Jiangui,Chau K T.A new efficient permanentmagnet vernier machine for wind power application[J].IEEE Transactions on Magnetics,2010,46(6):1475-1478.

[3]Li Xianglin,Chau K T,Cheng Ming,et al.An improved coaxial magnetic gear using flux focusing[C].Proceedings of International Conference on Electrical machine and system,Beijing,China,2011.

[4]Cheng Ming,Zhu Ying.The state of the art of wind energy conversion systems and technologies:a review[J].Energy Conversion and Management,2014,88:332-347.

[5]张建忠,程明.新型直接驱动外转子双凸极永磁风力发电机[J].电工技术学报,2007,22(12):15-21.Zhang Jianzhong,Cheng Ming.A novel outer-rotor permanent magnet generator with doubly salient structure for directly coupled wind turbines[J].Transactions of China Electrotechnical Society,2007,22(12):15-21.

[6]李祥林,程明,邹国棠,等.聚磁式场调制永磁风力发电机工作原理与静态特性分析[J].电工技术学报,2014,29(11):1-9.Li Xianglin,Cheng Ming,Chau K T,et al.Principle and analysis of a new flux-concentrating fieldmodulated permanent-magnet wind power generator[J].Transactions of China Electrotechnical Society,2014,29(11):1-9.

[7]李祥林,程明,邹国棠.聚磁式场调制永磁风力发电机输出特性改善的研究[J].中国电机工程学报,录用.Li Xianglin,Cheng Ming,Chau K T.Research on improvement of output characteristics of the fluxconcentrating field-modulated permanent-magnet wind power generator[J].Proceedings of the CSEE,in press.

[8]Lin D,Zhou P,Fu W N,et al.A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis[J].IEEE Transactions on Magnetics,2004,40(2):1318-1321.

[9]Katsumi Yamazaki,Atsushi Abe.Loss analysis of interior permanent magnet motors considering carrier harmonics and magnet eddy currents using 3-D FEM[C].IEEE International Conference on Electrical Machines and Drives,Antalya,Turkey,2007.

[10]Katsumi Ymazaki,Yuji Kanou.Rotor loss analysis of interior permanent magnet motors using combination of 2D and 3D finite element method[J].IEEE Transactions on Magnetics,2009,45(3):1772-1775.

[11]Huang Yunkai,Dong Jianning,Jin Long,et al.Eddycurrent loss prediction in the rotor magnets of a permanent magnet[J].IEEE Transactions on Magnetics,2011,47(10):4203-4206.

[12]Bastos J P A,Sadowski N.Electromagnetic modeling by finite element methods[M].London:CRC Press,2003.

[13]Pang Y,Zhu Z Q,Howe D,et al.Eddy current loss in the frame of a flux-switching permanent magnet machine[J].IEEE Transactions on Magnetics,2006,42(10):3413-3415.

[14]Stoll R L.The analysis of eddy currents[M].Oxford:Clarendon Press,1974.

[15]Stoll R L,Hammond P.Calculation of the magnetic field of rotating machines,part 4.approximate determination of the field and the losses associated with eddy currents in conducting surfaces[J].Proceedings of the IEE,1965,112(11):2083-2094.

[16]Andrada P,Torrent M,Perat J I,et al.Power losses in outside-spin brushess DC motor[J].Renewable Energy and Power Quality Journal,2004,4(2):320,5pages.

[17]Gieras J F.Permanent magnet motor technology:design and applications[M].London:CRC Press,2002.