屏蔽效能测试用双焦点平面腔的设计与应用

周 香 周忠元 沈军涛

（东南大学机械工程学院 南京 211189）

0 引言

随着电子技术的发展，对电子产品的电磁兼容性设计提出更高的要求。以无线通信为例，4G 移动终端的数据传输速率达100Mbit/s，其频率处于特高频（100MHz～3GHz）；而军用无线通信的最高使用频率处于超高频（3～30GHz）频段。

板状的屏蔽材料的屏蔽效能标准化测试方法主要有窗口法和法兰同轴法两种。MIL-DTL-83528C规定的窗口法的频率适用范围为0.02～10GHz，其需660mm×660mm 大小的试样，测试中需更换不同的天线。ASTM D4935—2010 规定的法兰同轴法的频率适用范围为30MHz～1.5GHz。此外，还得出了一些 1GHz 以上的新的测试方法，如扩展 ASTM D4935 的上限频率[1,2]、双脊喇叭天线法[3-5]、法兰式双脊波导法[6]、拱形法[7]和双焦点平面腔（Dual Focus Flat Cavity,DFFC）法[8-13]等。DFFC 就是一个横截面为椭圆的腔，由T.Tosaka 等[8]于2005 年提出。文献[10]构建了长轴、短轴和高度分别为280mm、243mm 和10mm 的DFFC，在焦点位置的两个长为10mm 的馈电针作为输入和输出，其工作频率范围为1～15GHz。文献[11]采用DFFC 评估材料的阻抗和屏蔽效能。文献[12]研制的新的双腔焦点平面腔上限使用频率达33GHz，其长轴、短轴和高度分别为200mm、173mm 和4.5mm。文献[13]对两个DFFC 进行了评估。

以上研究主要关注通过DFFC 测试的屏蔽效能（Shielding Effectiveness,SE）获得材料的薄膜电阻，并未对如何确定DFFC 尺寸进行深入分析，由文献[10,11]可见DFFC 上限频率确定的不确定性。

本文旨在通过对椭圆谐振腔谐振特性的分析确定腔体尺寸与上限频率的关系，进行双腔点平面设计，并研究时域门技术在DFFC 法屏蔽效能测试中的应用。

1 DFFC

1.1 DFFC 屏蔽效能测试原理

材料屏蔽效能测试用DFFC 是带有输入输出端口的椭圆柱腔，输入输出端口位于椭圆柱腔的焦点位置F1和F2，如图1 所示。

图1 双焦点法屏蔽效能测试装置示意图Fig.1 The diagram of SE test device based on dual focus method

从输入F1发出的电磁波经椭圆柱壁面反射，会聚到F2。在输入一定的情况下，通过比较未放置试样和放置试样F2处接收到的电压或功率，获得试样的电磁屏蔽效能。

1.2 椭圆谐振腔的谐振特性

移去焦点位置的输入输出端口，DFFC 就是椭圆谐振腔，可看成两端短路的椭圆波导。椭圆谐振腔的谐振会影响DFFC 的传输特性。

通常在椭圆柱坐标系中分析椭圆柱波导。在椭圆柱坐标系（ξ，η，z）中，焦距为2c 的椭圆，偏心率e 由1/coshξ0确定，谐振腔的长轴a=ccoshξ0，短轴b=csinhξ0，其中ξ＝ξ0构成谐振椭圆柱波导的横截面的边界。

文献[14]研究了椭圆柱波导中波的传播。假定波导由理想导体制成，内部填充理想介质。在椭圆坐标系中，Helmholtz 方程表示为

式中

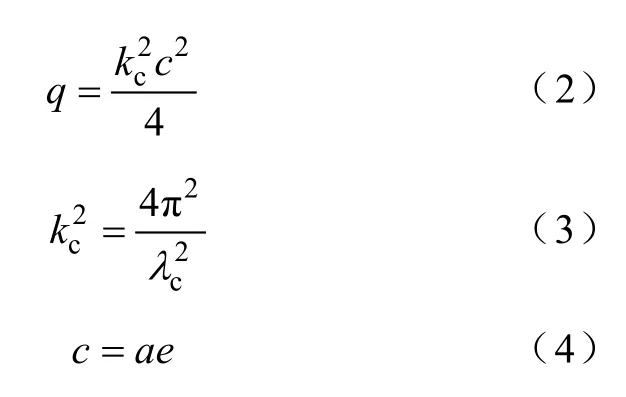
可通过分离变量法解得椭圆柱波导中的场分量。由z=0 和z=L 的边界条件，可由椭圆柱波导中的场分量推导出椭圆谐振腔中的场分量。在椭圆谐振腔中存在4 种模式，即TMcmrn、TEcmrn、TMsmrn、TEsmrn模，其中m,n=0,1,2,…，r=1,2,3,…，下标c表示偶模，s 表示奇模。各模式的谐振波长由式（5）确定。

式中，S 为椭圆的周长， S=4 aK (e)；K (e) 为第二类椭圆积分；R 为椭圆的等效直径D 与腔体高度L的比值，R=D/L；qcmr、qsmr分别为m 阶径向马丢偶函数、奇函数在ξ=ξ0的第r 个根[14]。

馈针是沿z 轴的，椭圆腔中的是TM 模(Hz=0)。n=0 时，TMmr0模中有3 个场分量:Ez≠0、Hξ≠ 0、Hη≠ 0，而Eξ=Eη=Hz=0。将n=0 代入式（5），得

由式（6）可见，n=0 时，谐振频率与R 和L无关，仅与横截面相关。n=0 时的谐振频率决定了DFFC 的最低工作频率，即采用较大横截面可获得较低的最低工作频率。当n=1 时，意味着在z 方向存在驻波，此时，电场方向垂直于壁面，坡印亭矢量平行于壁面，能量不会在壁面反射，导致DFFC两端口间的传输系数急剧减小。因此，TMmr1模的谐振频率决定了DFFC 的上限工作频率。文献[10,11]中的DFFC 分别标为DFFC1 和DFFC2，表1 和表2给出了其谐振频率。由表1 和表2 可见DFFC1 和DFFC2 的工作频率范围分别为1～15GHz 和1～33GHz。

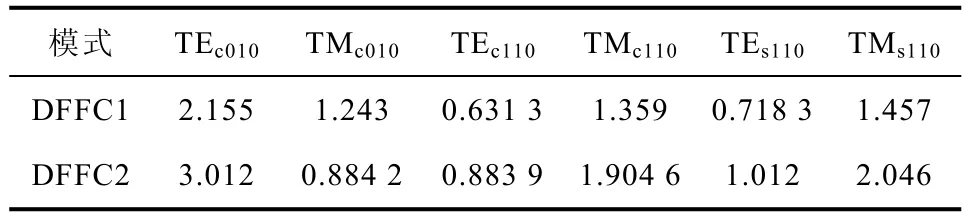
表1 n=0 时DFFC 谐振频率Tab.1 The resonant frequency of DFFC when n=0

表2 n=1 时DFFC 谐振频率Tab.2 The resonant frequency of DFFC when n=1

1.3 DFFC 的上限工作频率影响因素

由前面的分析可知TMmr1模的谐振频率决定了DFFC 的上限工作频率。下面以 TMc111为例，由式（5）可分析各因素对谐振频率的影响。由式（5）确定的不同R 值的 λ/S 与离心率e 的关系如图2 所示。由图2 可见，λ/S 对R 的变化较敏感，而对离心率e 不敏感。

表3 为椭圆的腔体高度L 固定为9mm、e 为0.46、R 在20～50 范围内时，椭圆谐振腔的最低谐振频率f（以下不特别说明谐振频率均指最低谐振频率）与椭圆周长S 和等效直径的对应关系。表4 为椭圆周长S 固定为771mm，R 在20～50 范围内，且R 值随L 的不同而变化，腔体高度L 与谐振频率f 的对应关系。

表3 表明椭圆周长S 在565.49～1 413.7mm（ΔS=842.1mm）范围内变化，而谐振频率f 基本不变（Δf=0.023GHz），即腔体高度L 固定，椭圆周长S 对谐振频率f 的影响很小；而从表4 中可见，腔体高度L 在3～18mm 范围内变化时，谐振频率f 在50～8.4GHz 范围内变化，即椭圆周长S 固定，腔体高度L 对谐振频率f 的影响较大。因此，腔体的周长不是TMmr1模谐振频率的主要影响因素，腔体高度才是TMmr1模谐振频率的主要影响因素。

基于以上分析，确定工作频率范围为1～18GHz的DFFC 的尺寸为:a=130mm、b=115mm、L=6mm，馈针长度为6mm，所设计的双焦点平面腔如图3 所示。定义该DFFC 为DFFC3。

表3 周长与谐振频率的关系Tab.3 The relation of perimeter to resonant frequency

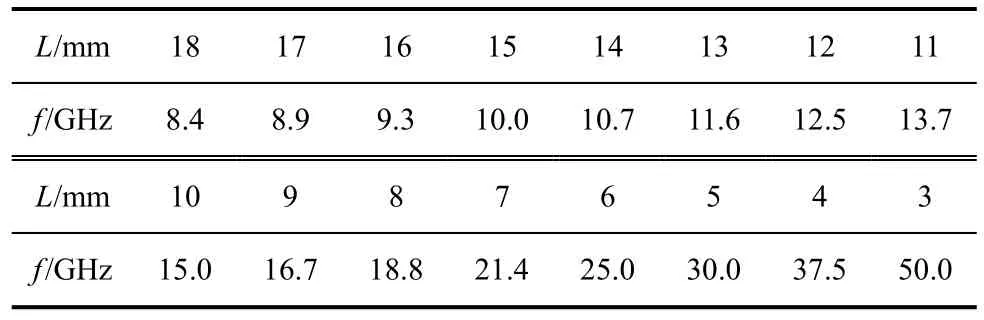
表4 高度与谐振频率的关系Tab.4 The relation of height to resonant frequency

图3 双焦点平面腔Fig.3 The DFFC

2 仿真与测试

在使用中关心的是DFFC 端口1 到端口2 之间的正向传输系数S21。通过3D 仿真软件对DFFC1、DFFC2 和DFFC3 进行仿真，获得的各装置的传输系数S21 如图4 所示。

图4 3 个DFFC 的S21 仿真值Fig.4 The simulation results of S21 of three DFFCs

图4 中各DFFC 的S21 下降的频点与表2、表4中的分析一致，即TMmr1模的出现是影响DFFC 传输性能的重要因素。为抑制高次模出现，保证足够的测试动态范围，定义高次模谐振频率的 80%为DFFC 的上限工作频率，在上限频率以下，S21＞10dB。从仿真可见，所设计的DFFC（DFFC3）满足1～18GHz 的设计要求。图5 为所设计DFFC3 的S21 测试值，结果表明在1～18GHz 内没有出现高次谐振。

图5 DFFC3 的S21 测试值Fig.5 The S21 test results of DFFC3

3 时域门技术在SE 测试中的应用

时域门在一定程度上可被看成是“具有带通功能的时域滤波器”，通过时域门可去除装置对测试结果的影响。在实际测试中可利用矢量网络分析仪的时域分析功能加载时域门，实现时域测量。本文的测试系统包括DFFC、矢量网络分析仪和两根电缆，如图6 所示。利用矢量网络分析仪测出有无试样时的时域S21，计算出材料的SE。

利用矢量网络分析仪进行时域测量S21 时，矢量网络分析仪首先在特定频率范围内按一定的步长进行扫描，测量S21 在不同频点上的值，从而得到频域的 S21。然后采用线性调频变换（Chirp-Z Transform，CZT）得到S21 的时域表示。在时域中利用时域门截取直接耦合部分变换到频域可得到滤除杂散干扰的S21。S21 测试结果如图7 所示，材料的SE 如图8 所示。

图6 DFFC 法SE 测试布置Fig.6 The layout of SE test based on DFFC method

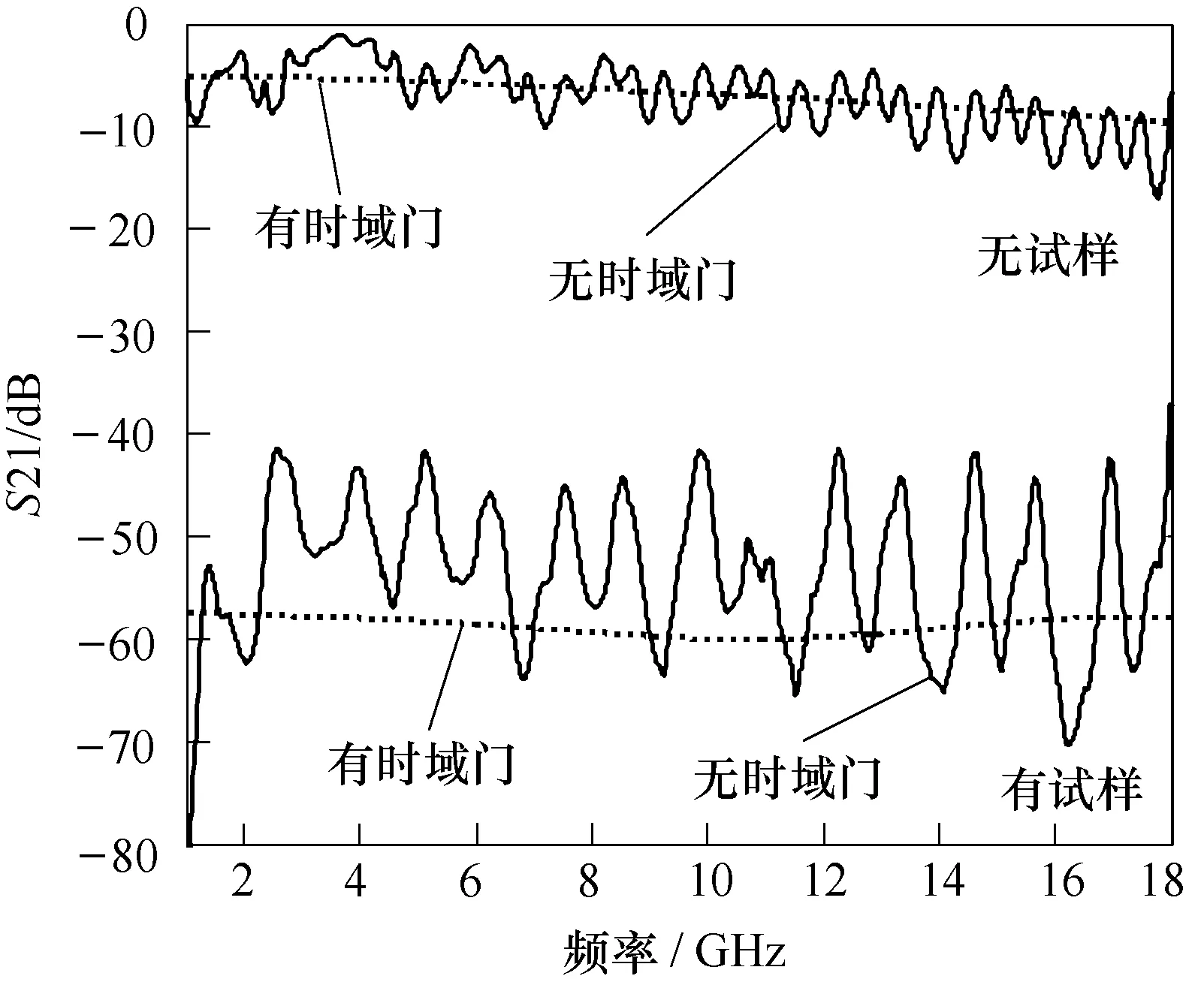
图7 不同状态DFFC 的S21 测试值Fig.7 The S21 test results with DFFC under different condition

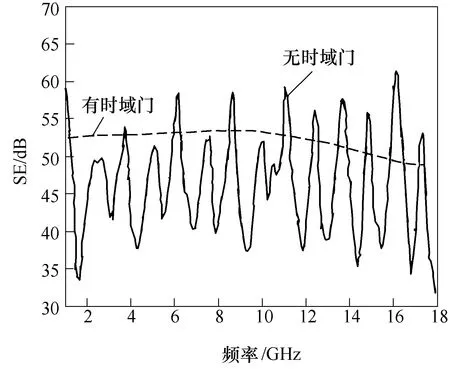
图8 基于DFFC 法的材料SE 测试值Fig.8 The SE test results based on DFFC

在DFFC 测量系统中，通过时域门滤除直射波，保证汇集在端口2 的波的相位相同。此外，由于不同试样的SE 和吸收损耗不同，壁面多次反射的次数不同，因此，时域门技术还可减少测试的不确定性，使测量结果更稳定、更可信。

通过多种试样的多次测试，所构建的DFFC 测试系统测试动态范围为60dB，不确定度为2.6dB。测试可重复性误差和再现性误差分别为1.2dB 和1.3dB。

4 结论

本文从椭圆腔的谐振理论出发，分析了双腔点平面腔的使用频率范围。由分析可知谐振波长与椭圆周长之比 λ/S 对椭圆等效直径D 与腔体高度L 之比R 的变化较敏感，而对离心率e 不敏感；相对于腔体周长，腔体高度是高次模的主要影响因素；可由出现高次模（TMmr1模）的频率确定DFFC 的上限工作频率。仿真和测试表明所设计DFFC 满足1～18GHz 的工作频率要求。本文分析方法可用于DFFC的设计指导。

采用所制造的1～18GHz DFFC，利用时域门进行基于DFFC 法的材料SE 测试分析，测试结果稳定、可靠。

[1]Hong Y K,Lee C Y,Jeong C K,et al.Method and apparatus to measure electromagnetic interference shielding efficiency and its shielding characteristics in broadband frequency ranges[J].Review of Scientific Instruments,2003,74(2):1098-1102.

[2]Sarto M S,Tamburrano A.Innovative test method for the shielding effectiveness measurement of conductive thin films in a wide frequency range[J].IEEE Transactions on Electromagnetic Compatibility,2006,48(2):331-341.

[3]Marvin A C,Dawson L,Flintoft I D,et al.A method for the measurement of shielding effectiveness of planar samples requiring no sample edge preparation or contact[J].IEEE Transactions on Electromagnetic Compatibility,2009,51(2):255-262.

[4]Jacobs I S,Bean C P.Fine particles,thin films and exchange anisotropy[J].in Magnetism,1963,3:271-350.

[5]Catrysse J.Shielding effectiveness of flat samples and conductive gaskets:new measuring cell for the frequency range 1-18GHz[C]//IEEE International Symposium on Electromagnetic Compatibility,Detroit,MI,2008:1-6.

[6]Kwon J H,Choi H D,Choi J I,et al.Development of apparatus for measuring electromagnetic shielding effectiveness at GHz frequency band[C]//IEEE International Symposium on Electromagnetic Comp-atibility,Honolulu,HI,2007:1-4.

[7]Dvurechenskaya N,Zielinski R J.Advantages and disadvantages of the free-space arch method used for investigation of shielding materials at low gigahertz frequencies[C]//10th International Symposium on Electromagnetic Compatibility,York,2011:790-795.

[8]Nishikata A,Tosaka T,Fukunaga K,et al.Shielding effectiveness measurement using dual-focus flat cavity at microwave frequency range[J].Transactions of the Institute of Electronics Information &Communication Engineers B,2008,91:88-94.

[9]Tosaka T,Nishikata A,Fukunaga K,et al.Measurement of shielding effectiveness in the microwave frequency range using a dual focus flat cavity[C]//IEEE International Symposium on Electromagnetic Compatibility,Honolulu,HI,2007:1-4.

[10]Tosaka T,Nishiakta A,Fukunaga K,et al.Shielding effectiveness measurement for anisotropic materials using DFFC[C]//Proceedings of ISAP,Niigata,Japan,2007:93-96.

[11]Tosaka T,Nishiakta A,Fukunaga K,et al.Method for estimating sheet resistance of thin shielding sheets using DFFC[C]//Proceedings of GA of URSI,CD Proceedings (BP10),Chicago,2008.

[12]Tosaka T,Nishiakta A,Fukunaga K,et al.Method for sheet resistance estimation up to 33GHz using DFFC[C]//International Symposium on Electromagnetic Compatibility-EMC Europe,Athens,2009:1-4.

[13]Tosaka T,Nishiakta A,Fukunaga K,et al.Evaluation of system for estimating sheet resistance using DFFC[C]//URSI International Symposium on Electromagnetic Theory,Berlin,2010:81-84.

[14]Kretzschmar J G.Wave propagation in hollow conducting elliptical waveguides[J].IEEE Transactions on Microwave Theory and Techniques,1970,18(9):547-554.