基于优化模型的停车场规划设计分析

高新涛 陈 丽

（1.河南工业技师学院，河南 郑州 450007；2.中原工学院信息商务学院，河南 郑州 450007）

自21世纪以来，家用小汽车以惊人的速度进入普通居民家庭。由此引发了一系列问题，其中停车问题就是越来越突出的问题之一。停车场规划是指在有限的空间区域内，考虑诸如平均车位所占面积，车辆出入车位难易程度，停车场内部道路畅通程度等诸多因素，设计车位布局，尽可能多地发挥空间效率与时间效率。

目前，国内外对停车场的设计已做了一些工作，如车辆停放的设计规范，最小转弯半径，斜列式停放角度优化等。但是，对停车场的优化设计还存在着很多问题和不足：

①对停车场最佳排数没有进行优化设计，大多直接给定排数。

②每排最佳停放角度没有进行优化设计，而是将整个停车场设计成按同一角度停放。

本文设计出了使停车场时间和空间利用率更高的优化模型，在此模型中对停车场最佳排数及每排最佳角度进行了优化设计，以使在有限的空间停放更多的车辆，且车辆能够自由出入。通过实验证明了该模型的有效性。

1 停车位与通道设计

本文以桑塔纳为例。根据实际调查，桑塔纳的长度为4.68m，宽度为1.7m。停车场中标志线的宽度为0.1m，所以停车场中停放轿车需要长5m，宽2.2m的位置（其中包括0.1m的标志线宽度）。

轿车的最小转弯半径为5.5m（最小转弯半径:汽车转弯时转向中心到汽车外侧转向车轮轨迹间的最小距离），所以通道的最小宽度为R=5.5-2.4cosθ.其中为停车位的长边与通道的夹角［1］。

如图1所示，L为垂直于通道方向的停车位长，即停车带宽度，W为平行于通道方向的停车位宽，Ld表示停车位末端的距离，它们分别是角θ的函数。且有

图1 停车位与通道设计

2 停车场单排车位优化设计

2.1 平行式排放

当车辆以平行式排放成一排时，车辆与通道的夹角θ=0，此时通道宽度R=5.5-2.4cos0=3.1m，车位长度L=2.2米，宽度W=5+1.2=6.2m。停车场宽度需B=R+L=5.3m，停车位个数为（A为停车场长度），如图2所示。

图2 平行式排放

2.2 垂直式排放［2］

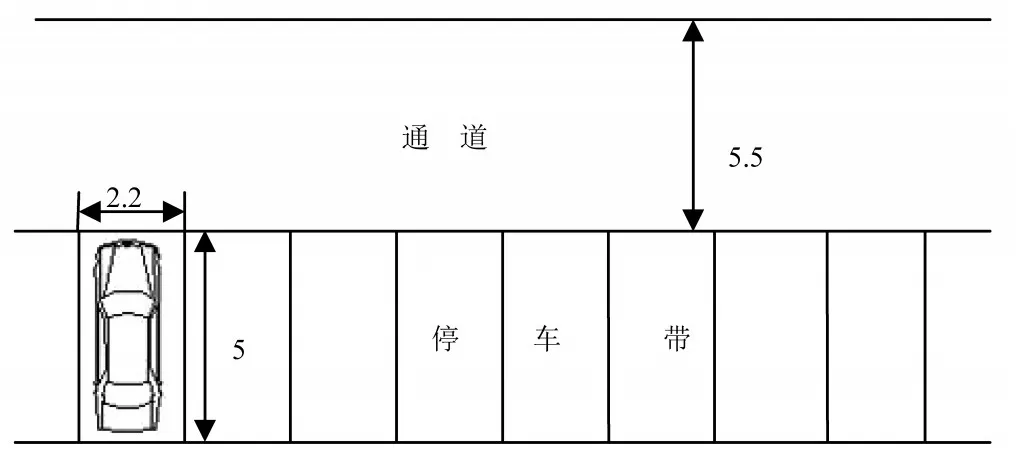
图3 垂直式排放

2.3 斜列式排放

当车辆以斜列式排放成一排时，如图4所示，车辆与通道的夹角θ满足：，此时通道宽度为R=5.5-2.4cosθ，车位长度 L=5sinθ+2.2cosθ，宽度W=2.2/sinθ，停车场宽度需为 B=R+L=5.5-0.2cosθ+5sinθ（5.3＜A＜10.5），停车位末端的距离为Ld=5cosθ+2.2cotθcosθ，停车位个数为。

图4 斜列式排放

当5.3＜B＜10.5时，停车位排布方式有四种方案可选：①单排平行式排放；②单排斜列式排放；③两排平行式排放；④两排斜列式排放。可根据停车场长度A的值来选择最佳排布方式。

3 停车场停车位排数和排布方式优化模型

本文停车位均按小型轿车设计。

设A为停车场长度，B为停车场宽度，C为停车带两端的纵向通道宽度，第i区是指第i个通道及两侧的停车带，xi是指第i区停车位个数（i=1,2,…,n），n为通道个数，m为停车位排数。为使停车场空间利用率最高，位于同一个区的汽车停车角度θ相同［3］。

①当m=2n时，即每个通道两侧都设有停车带时，优化模型为：

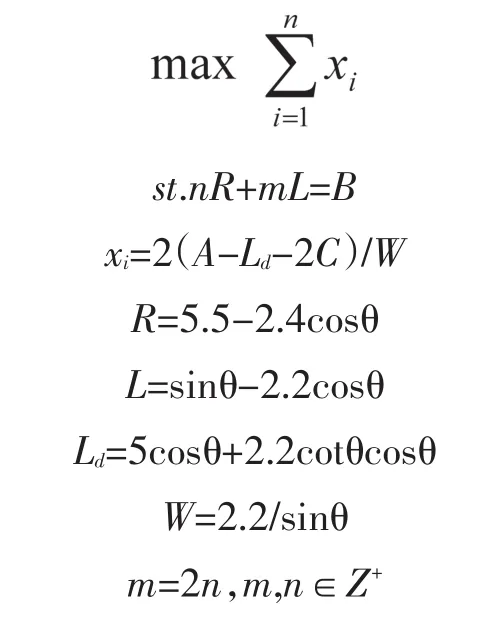
②当m=2n-1时，即前n-1个通道两侧都设有停车带，第n个通道只有一侧设有停车带时，优化模型为：

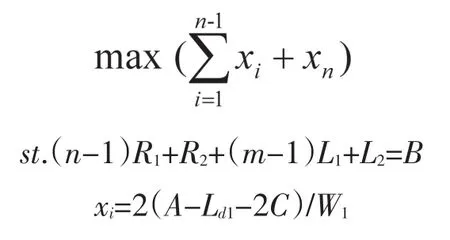
其中，R1为前n-1个通道宽度，R2为第n个通道宽度，L1,W1分别为前n-1区停车位长度和宽度，L2,W2分别为第n区停车位长度和宽度。Ld1表示前n-1区停车位末端的距离，Ld2表示第n区停车位末端的距离，θ1为前n-1区停车位的长边与通道的夹角，θ2为第n区停车位的长边与通道的夹角。

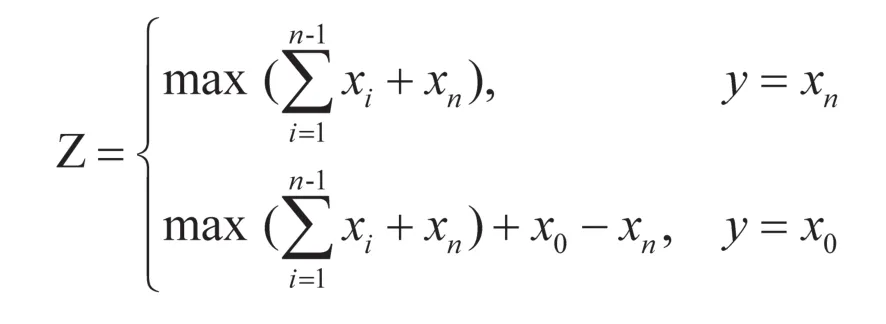
通过模型（1），（2），分别计算出停车场按偶数排和奇数排规划时停车位最大个数及Z，进行比较。若X≥Z，则选用模型（1），否则，选用模型（2）。

4 停车场优化设计案例分析

某居民小区的一个露天停车场长61.76m，宽46m，请对该停车场停车位进行规划设计，使停车数量最多。

①当m=2n时，即每个通道两旁都设有停车带时，令C=6米，优化模型为：

st.nR+mL=n（5.5-2.4cosθ）+m（5sinθ+2.2cosθ）=46

xi=2（61.76-Ld-12）/W=（61.67-5cosθ-2.2cotθcosθ-12）sinθ/1.1，

m=2n，m,n∈Z+

②当m=2n-1时，即前n-1个通道两旁都设有停车带，第n个通道只有一侧设有停车带时，优化模型为：

st.（n-1）R1+R2+（m-1）L1+L2

=（n-1）（5.5-2.4cosθ1）+（5.5-2.4cosθ2）

+（m-1）（5sinθ1+2.2cosθ1）+（5sinθ2+2.2cosθ2）

=37.26

xi=2（61.76-Ld1-12）/W1=（61.76-5cosθ1-2.2cotθ1cosθ1-12）sinθ1/1.1

xn=（61.76-Ld2-12）/W2=（61.76-5cosθ2-2.2cotθ2cosθ2-12）sinθ2/1.1

m=2n-1，m,n∈Z+

本文采用Lingo软件对模型（1）、（2）分别进行计算，结果为：

表1 模型（1）运行结果

表2 模型（2）运行结果

比较模型（1），（2），得模型（1）优于模型（2），所以我们应将停车场分为6个横排式停车带，每个停车带停车位倾角约为63.32°。

停车场规划及行车路径见图5。

图5 停车场规划图

5 结语

本文首先对平行式、垂直式、斜列式三种停放方式单排停放时所需通道宽度、车位长度、宽度等进行了分析；然后，在此基础上设计出了停车场最佳排数及最佳停放角度优化模型。该模型在保证车辆能够安全自由进出条件下，使有限的空间中停车位个数达到最大化。通过对某特定停车场的规划设计，证明了模型的有效性。

［1］宋作忠，何文章.基于遗传算法的交易中心停车场优化设计［J］.数学的实践与认识，2004（34）:19-23.

［2］何文章，宋作忠.数学建模与实验［M］.黑龙江：哈尔滨工程大学出版社，2002.

［3］韩中庚.数学建模方法及其应用［M］.北京：高等教育出版社，2009.