基于排队论的修船码头移泊调度系统

唐伟炜，杨坤荣，艾志兴(.华南理工大学 土木与交通学院，广东 广州 5064;.中船澄西船舶(广州)有限公司，广东 广州 546;.中船黄埔文冲船舶有限公司，广东 广州 5075)

基于排队论的修船码头移泊调度系统

唐伟炜1，杨坤荣2，艾志兴3
(1.华南理工大学 土木与交通学院，广东 广州 510641;2.中船澄西船舶(广州)有限公司，广东 广州 511462;3.中船黄埔文冲船舶有限公司，广东 广州 510715)

修船码头移泊调度是修船厂作业的重要组成部分，文章基于排队论对修船码头移泊调度系统进行分析，阐述了该系统的排队流程，并建立了修船码头移泊调度排队模型，研究了码头泊位调度系统的运行效率，确定系统参数的最优值，以决定系统的结构是否合理，设计改进的措施等。

修船码头；排队论；系统分析；容量有限排队模型

排队论是20世纪初由丹麦数学家Erlang研究并发展起来的一门学科，也称随机服务系统理论。通常是建立一些数学模型，对系统状态可能发生改变的事件进行描述，并对系统的状态进行预测。发生系统状态改变的事件通常有2个，一是顾客到达，二是系统提供服务[1]。现实生活中排队的现象有很多，如到餐厅用餐、轮船进港、病人就诊、商店购物等。排队论主要通过对队长、等待时间以及忙期分布的研究，判断一个已知的系统中用什么样的模型，然后利用排队理论对系统进行分析，最后解决系统的最优设计和最优运行问题。

1 修船码头移泊排队系统的构成

1.1修船码头具有排队系统的典型特征

1)有请求服务的人或物——请求进厂的船舶，我们将此称为“顾客”。

2)有为顾客提供服务的人或物——修船码头，我们称此为“服务员”，修船码头所提供的服务即为为请求进厂的船舶安排泊位停靠,而每条船都尽量停在它的最佳工作泊位，最佳工作泊位能保障船舶按期完成作业，我们称最佳工作泊位为服务台，这些泊位往往是重合的，基本上是靠近码头岸线的档位，由船舶和码头组成服务系统。

3)船舶随机地一艘艘或一批批要求进厂，每艘船只有停泊在最佳工作泊位才能开始作业，而每艘船作业的时间不一定是确定的，服务过程的这种随机性不仅会造成某个阶段船舶排长队等待最佳工作泊位，而某些阶段码头又有很多空闲泊位，造成泊位利用率低下。

1.2组成部分

将码头移泊调度看作一个排队系统，它由以下3部分组成。

1)输入过程，在修船码头移泊调度系统中，输入过程指即船舶来到码头的概率分布。系统首先要根据船期表，由船舶到达的规律作出经验分布，然后根据统计方法确定理论分布，并估计它的参数值。 如在某一周期内，船舶进厂服从泊松分布，且船舶的到达是相互独立的、平稳的输入过程。

2)排队规则，即顾客排队和等待的规则。排队规则一般有即时制和等待制2种。在修船码头移泊调度系统中，船舶遵循的是混合制规则，即最佳工作泊位被占用时，船舶排队等候泊位安排，但又不允许队列无限长，排队的船舶一般遵循先到先服务的次序规则，但当有紧急任务时则遵循有优先权服务的次序规则。

3)服务机构，修船码头有多个泊位，但每个泊位只能停泊一艘船舶。和输入过程一样，多数的船舶作业时间都是随机的，如果我们假定船舶作业时间的分布是平稳的，那么若以Tn表示第n艘船作业所需的时间，则船舶作业时间所构成的序列{Tn}，n=1，2，…所服从的概率分布表达了移泊系统的服务机制，一般假定船舶的作业时间T1，T2，…是独立分布的，并且任意2艘船舶到来的时间间隔集合{Tn}也是独立的。

1.3系统参数

研究修船码头移泊调度排队问题的目的，是研究该系统的运行效率，确定系统参数的最优值，以决定该移泊系统的结构是否合理。

衡量码头运行效率的指标通常有系统服务能力，系统状态概率，船舶队长，船舶等待队长，船舶逗留时间，船舶等待时间等[2]。除此之外，需考虑的指标还有系统的忙期以及输出过程。系统的忙期是指从船舶到达较为空闲的码头时起，到码头再次恢复空闲的这一段时间长度，即修船码头连续工作的时间长度(这里的空闲指码头没有进行泊位安排的工作)。它与码头连续工作的时间长度以及码头的工作强度有关。忙期的长度和一个忙期中平均完成泊位停靠的船舶艘数，这些都是衡量码头泊位调度系统服务效率的指标。而输出过程则是船舶离开码头的过程，主要指标有船舶离开码头的时间间隔以及一定周期内离开码头的船舶艘数。

修船码头的泊位调度排队系统如图1所示。

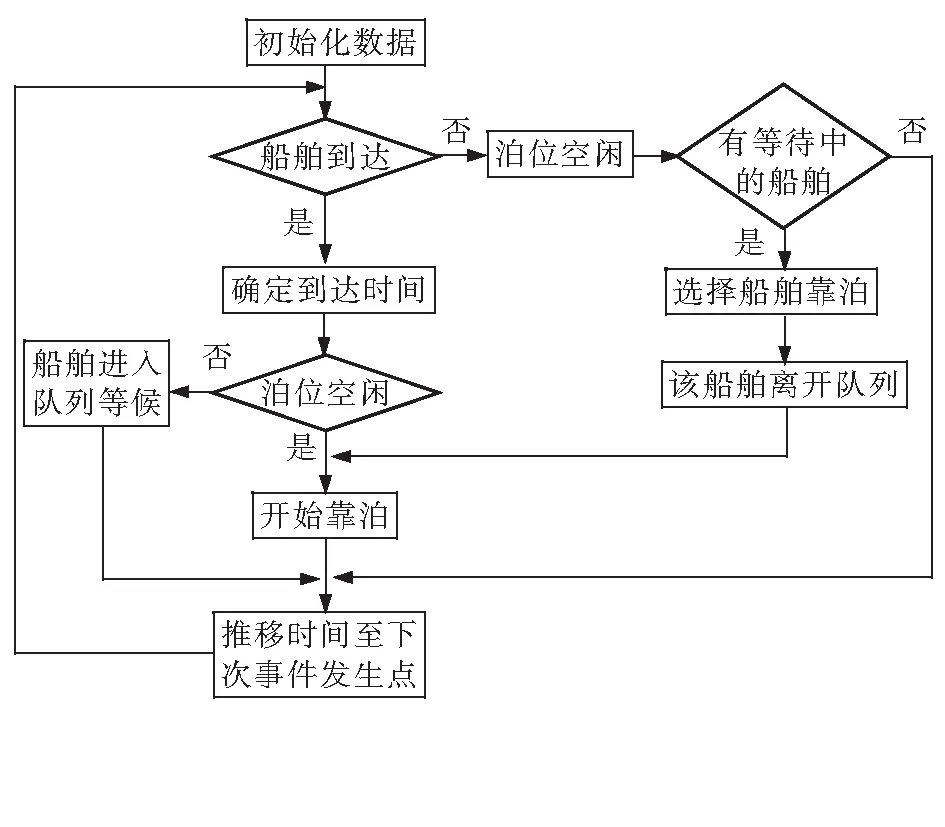
图1 修船码头排队系统框图

排队系统还存在以下重要参数。

1)队长：指码头移泊调度系统中的船舶艘数，它的期望值记为Ls；排队长，指在系统中排队等待作业的船舶艘数，其期望值记为Lq。

系统中的船舶艘数 = 等待服务的船舶艘数 + 正被服务的船舶艘数。

由此可判断出，Lq(或Ls)越大，服务的效率则越低。

2)逗留时间：指某一艘船在码头的停留时间，即船舶从进厂到泊位安排完毕的时间。其期望值记Ws。等待时间，指某一艘船舶在开始作业之前等待的时间，其期望值记为Wq。

船舶逗留时间 = 船舶等待时间 +船舶被服务时间。

计算这些参数必须知道泊位调度系统状态的概率，即在t时刻码头的船舶艘数。如果在t时刻码头有n艘船，就说系统的状态是n，其概率一般用Pn(t)表示。

2 修船码头泊位调度系统的排队模型

对于修船移泊系统来说，输入过程为船舶独立到达且间隔时间服从一般概率分布，系统有多个泊位，即多个服务台，船舶所需的服务时间服从一般概率分布且是相互独立的。当系统处在旺季时，进厂船舶较多，相对最佳工作泊位来讲我们可以认定顾客源为无限，此时船舶需要排队等待最佳工作泊位，因工作周期有限，等待时间越久，后续工作时间越紧张，越不容易在计划周期内完成任务，船东和企业都要接受损失。又因码头不能无限制的使用泊位停船，容量有限而要求进厂船舶超出系统最大容量时，后来的船舶将被拒绝进入系统，系统将有损失率。如何使两者之间达到一个平衡，如何确定系统参数的最优值，是此模型将要研究的问题；另一种情况是系统处在淡季时，一个时期内进厂船舶有限，当进厂船舶艘数小于最佳工作泊位艘数时，船舶无需排队等待可直接进入系统开始作业。

为更清晰的表达修船码头泊位调度系统的排队模型，一律设系统的输入过程服从泊松分布，即在t时刻,到达n艘船舶的概率为:

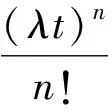
(1)

式中：λ为船舶平均到达率,即单位时间内(通常为24 h内)平均到达码头的船舶艘数。

设船舶作业时间服从参数为μ的负指数分布。因系统处于淡季时，船舶艘数小于最佳工作泊位数量，无需排队等待可直接作业，基本能在计划周期内完成任务，因此在此研究系统处于旺季时的状态，系统排队模型表达形式为M/M/C/N/∞[3]。

M/M/C/N/∞模型是指最佳工作泊位有限，但计划进厂船舶为无限，船舶到达相互独立， 到达过程是平稳的，进厂船舶流为泊松流，平均到达率为λ(单位时间到达船舶艘数)，到达数量为n，多服务台、先到先服务。假设码头有C个泊位为最佳工作泊位，系统的最大容量为N(N≥C)，各泊位的船舶靠泊时间满足负指数分布，且各泊位停泊作业是相互独立的(不搞协作)，船舶服务率为μ(单位时间服务船舶艘数)，当系统客满(即有N艘船计划进厂)时，有C个接受服务，总服务率：当 0lt;nlt;C时为nμ；当n≥C时为Cμ， 系统的服务强度为ρ=λ/Cμ，最佳工作泊位一般为最靠近码头岸线的2个档位，其艘数与船舶长度有关，即

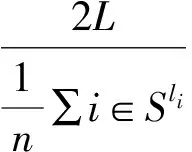
(2)

式中：L为码头岸线长度；li为船舶i的长度；S为船舶集合。

可以得到系统的状态概率平衡方程并由递推关系可得系统状态概率：

k=0,1,2,…,C-1,

(3)

(4)

系统的运行指标：

Ls=Lq+Cρ(1-PN),

(5)

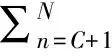
(6)

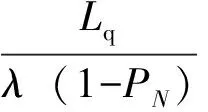
(7)

Ws=Wq+1/μ,

(8)

式中：P0为初始时刻系统状态概率；Pn为到达n艘船舶时系统状态概率；PN为到达船舶艘数达到系统极限时系统的状态概率；Ls为队长，即所有系统中船舶艘数；Lq为系统中排队的船舶数量；Ws为船舶在系统中的逗留时间；Wq为船舶等待时间。

3 算例

某码头的最佳工作泊位为10，系统容量为30。在某一时期，船舶的到来服从泊松分布，且λ=2(平均每天到达2艘船)，船舶进入码头作业时间服从指数分布，且μ=0.1(平均每天服务0.1艘船)，则ρ=2。

由式(3)可知系统的状态概率P0=1.69×10-13，即整个码头空闲的概率为1.69×10-13。

当n=5时，0≤n≤C，Pn=4.5×10-9；

当n=10时，0≤n≤C，Pn=4.8×10-7；

当n=20时，C≤n≤N，Pn=4.9×10-4；

当n=30时，C≤n≤N，Pn=PN=0.5。

当n=35时，对于M/M/C/N/∞模型，如果码头已有N艘船舶，则后来的船舶将被拒绝，于是可设PN为被拒绝的概率，1-PN即为接受船舶进厂的概率。λ(1-PN)表示一定周期内实际进入码头的船舶艘数，在稳定状态下，即为一定周期内实际完成靠泊的船舶艘数。系统满员的损失率：

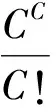
(9)

若想船舶等待时间越小，在最佳工作泊位艘数，系统容量，λ和μ一定的情况下，则排队船舶艘数要越少，但是进厂船舶艘数减少直接影响船厂的效益，因此要考虑当船舶总数为多少时才能使系统达到最优的效果。

由式(5)、式(6)可知，系统船舶排队的艘数Lq=19，Ls=29，即，当系统中船舶总数为29，排队船舶艘数为19时，系统的状态能达到最优。此时Pn=0.25，Wq=19，Ws=29。

即船舶平均排队时间为19天，船舶平均逗留时间为29天。

4 结束语

本文在排队理论的基础上对修船码头移泊调度系统进行了分析，将移泊系统分成输入过程，服务过程，输出过程等。并通过一些指标来衡量码头系统的工作效率，来判断系统结构是否合理。最后针对系统的M/M/C/N/∞模型进行模拟仿真计算，得出了使系统状态效率最佳的参数数值。

[1] 王庚，王敏生. 现代数学建模方法[M]. 北京：科学出版社，2010.

[2] 唐应辉，唐小我. 排队论一基础与分析技术[M]. 北京：科学出版社，2006.

[3] 孙荣恒,李建平.排队论基础[M].北京：科学出版社，2002.

Ship berth scheduling is an important part of shipyard.This article studies on the berth scheduling problem based on the queuing theory,expounds the queuing process of the system and the berth scheduling system queue model is established.Running efficiency of the berth scheduling system is studied and the optimal value of system parameters is determined,which may decide whether the system structure is reasonable and design the improvement measures.

ship-repairing dock;queuing theory;system analysis;M/M/C/N/∞ model

U673

10.13352/j.issn.1001-8328.2015.05.014

唐伟炜(1983-)，女，天津人，在读博士研究生，研究方向为船舶与海洋结构物设计制造。

2015-06-01