兰新铁路西宁站弹性边界条件钢结构楼梯设计研究

张亚娟

(中铁第一勘察设计院集团有限公司城建院， 西安 710043)

兰新铁路西宁站弹性边界条件钢结构楼梯设计研究

张亚娟

(中铁第一勘察设计院集团有限公司城建院， 西安 710043)

针对目前大型火车站常用的大跨度钢楼梯结构采用独立计算模型与站房结构联合计算模型进行分析对比，揭示了楼梯结构在考虑支座复杂边界条件下杆件内力及自振特性的差异。结果表明，支座刚度对楼梯结构的内力及自振特性影响显著，是结构设计中不可忽略的重要因素。同时，建议类似工程楼梯结构设计应采用与主体结构联合分析的方法，以获得在复杂边界条件下楼梯结构真实的力学响应。

铁路客站；楼梯结构；独立分析；联合分析；自振周期；特征值分析；Ritz向量法

1 工程概况

图2 钢楼梯剖面(单位：mm)

西宁火车站工程为在建的大型旅客站房之一，采用高架候车的客流组织模式，旅客候车层在车场上方，层高10 m，站房入口进站大厅至候车层主通道楼梯宽度为8 m，总跨度25.72 m，为满足站房进站大厅的整体建筑效果及楼梯下部空间的使用功能要求，仅在根部设置支撑柱[1]。考虑到主通道楼梯跨度大，同时大型旅客站房的人流量集中，楼梯活荷载较大，因此普通的钢筋混凝土结构不再适用，设计中采用钢结构梁式楼梯结构形式。钢楼梯上、下部支座及根部支撑柱均设置于钢筋混凝土结构楼面。由于钢楼梯平面跨度较大且楼面混凝土结构各部位竖向刚度存在差异，因此设计与常规混凝土结构楼梯不同，需考虑弹性边界的不利影响[2，3]，增加了楼梯钢结构设计的复杂性，同时为了保证旅客上下通行的舒适度要求，需要对弹性边界钢楼梯结构振动频率进行控制[4]。

2 钢楼梯结构布置及设计荷载取值

2.1 楼梯结构布置

如图1、图2所示，钢楼梯采用梁式楼梯布置方式，4根楼梯折梁间距2.55 m，在根部设置钢筋混凝土楼梯柱将楼梯梁分为18.65 m及7.07 m两跨，上部焊接钢踏步板。楼梯梁下支座及楼梯柱均支承于一层楼面结构，上支座支承于二层楼面梁；上部支座采用单向滑动铰支座，其余支座形式均为固定铰支座[5]。楼梯梁截面尺寸为1 100 mm×350 mm×12 mm×20 mm，为焊接箱形截面。

图1 钢楼梯结构布置(单位：mm)

2.2 钢楼梯计算主要考虑的荷载工况

恒载按照各部位建筑装修作法计算，取3.0 kN/m2，活载根据《建筑结构荷载规范》(GB50009—2012)[6]，取3.5 kN/m2。

3 结构分析及对比

3.1 支座刚度对楼梯梁内力的影响

由于楼梯梁支座均设置于大跨度钢筋混凝土楼面上，支座刚度及楼面荷载对楼梯梁内力存在影响，设计中采用独立分析模型及与楼面结构联合分析模型两种情况进行对比分析，结果见图3～图10，限于篇幅仅给出自重及恒载作用下楼梯梁轴力及弯矩对比，图中给出楼梯梁每一段内力最大值或存在变号情况的最大、最小值，负值为轴压力或负弯矩。

图3 自重作用下楼梯梁轴力(独立模型)(单位：kN)

图4 自重作用下楼梯梁轴力(联合模型)(单位：kN)

图5 恒载作用下楼梯梁轴力(独立模型)(单位：kN)

图6 恒载作用下楼梯梁轴力(联合模型)(单位：kN)

图7 自重作用下楼梯梁弯矩(独立模型)(单位：kN·m)

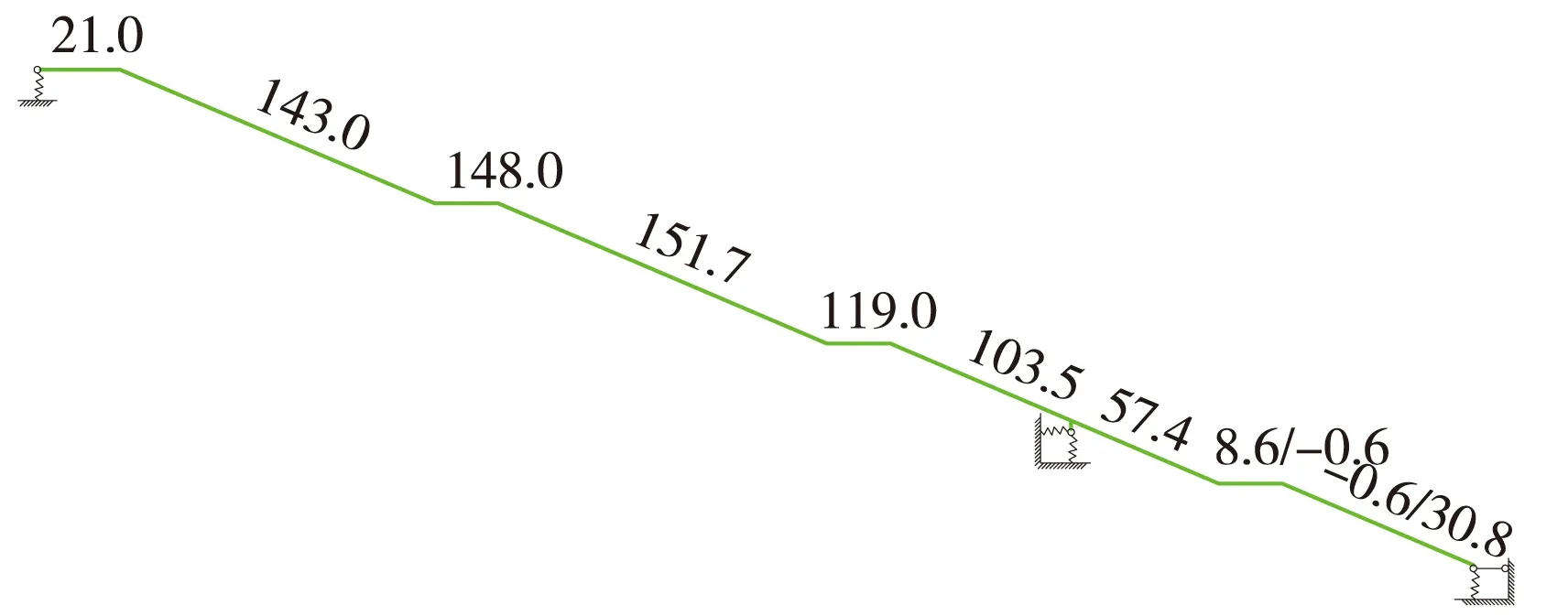
图8 自重作用下楼梯梁弯矩(联合模型)(单位：kN·m)

图9 恒载作用下楼梯梁弯矩(独立模型)(单位：kN·m)

图10 恒载作用下楼梯梁弯矩(联合模型)(单位：kN·m)

由图3～图6可知，独立模型中在自重及恒载作用下楼梯梁大跨段上部以轴向拉力为主，下部以轴向压力为主；小跨段均为轴向拉力。联合模型中楼梯梁大跨段主要以轴向压力为主，但每一斜段均会出现轴向拉、压变号情况，在靠近中间支座处局部出现较大拉力；小跨段以轴向拉力为主，斜段仍会出现轴向拉、压变号情况，最大拉力均出现在下部支座处。

由图7～图10可知，独立模型中在自重及恒载作用下楼梯梁弯矩为两跨连续梁弯矩分布特征，最大正弯矩在大跨跨中位置，最大负弯矩在中间支座位置，由于楼梯梁两跨跨度差异较大，小跨段主要为负弯矩，仅在根部出现正弯矩。联合模型中自重作用下楼梯梁弯矩差异很大，表现为简支梁弯矩分布特征，最大弯矩出现在大跨梁段跨中位置，在中间支座处未出现负弯矩。恒载作用下符合连续梁弯矩分布特征。

结合表1分析，在自重作用下由于中间支座处楼面结构变形较大，失去支撑作用，因此楼梯梁呈现简支梁弯矩分布，在恒载作用下，3处支座变形较为均匀，中间支座仍发挥作用，因此弯矩分布与独立模型计算结果相同，跨中弯矩差异不大，由于中间支座变形最大，因此该处负弯矩有所减小。对比独立模型计算结果，楼梯梁中轴力主要为拉、压性质的变化，由于支座变形差异的影响，使得梁段轴力分布不再单一，在自重作用下轴力数值也有所增加，最大值本应出现在中间支座位置而转移至下部支座位置。

表1 联合计算模型支座变形 mm

3.2 支座刚度对楼梯结构竖向自振频率的影响

(1)为保证结果的准确性，计算中采用板单元建立楼梯结构的计算模型，并与梁单元模型进行结果对比校准(图11)，再将梁单元置于站房整体结构中进行计算，以考察支座刚度对楼体结构竖向自振频率的影响[2]。

图11 楼梯结构板单元计算模型

结构振动特征值分析采用Ritz向量法，计算质量取结构自重及恒载，保证振型参与质量达到90%以上。Ritz向量法的特点是把外部荷载的空间分布特点与结构自身的几何、物理特性相结合，剔去对荷载没有响应的结构低阶模态，从而有效提高计算效率。使用荷载相关的Ritz向量法是对承受动力荷载结构中的精确节点位移与构件内力进行求解的最有效方法[7]。由于本文主要考察楼梯结构竖向振动特性，为保证计算的准确性，特征值分析中应提高竖向初始荷载向量数量[8-9]。板单元模型分析振型数34个，其中竖向荷载向量取30个；梁单元模型振型数16个，其中竖向荷载向量取12个。两个分析模型周期计算结果对比见表2。

表2 板单元模型与梁单元模型计算周期对比

选取两个计算模型模态分布相同的前6阶振型进行对比，除第3振型(Y向平动)周期比稍大以外，其余振型周期比均为0.9左右， 以板单元计算模型为基准说明梁单元计算模型的竖向自振频率约为板单元模型的0.9，刚度稍弱，以此来校准在梁单元模型中振动质量分布、加载方式及边界条件设置的一致性。

(2)将钢楼梯梁单元模型置于站房结构整体模型中进行计算[10]，质量分布及边界条件与独立模型完全相同，以考察楼梯结构弹性边界对竖向自振周期的影响，见图12。

图12 楼梯与站房结构联合计算模型

在联合计算模型中取分析振型数16个，竖向振动有效质量系数94.7%，前8阶振型均为站房结构整体振动，楼梯结构振动从第9阶开始，结果见表3。

表3 联合模型中楼梯结构计算周期

分析结果表明：(1)楼梯结构振型分布受站房整体结构影响很大，振型分布与独立模型不同，相互干涉作用明显；(2)在联合模型中受站房主体结构影响，楼梯结构竖向振动主要以一阶平动振型为主；(3)由于存在边界刚度的影响，楼梯结构自振周期较独立模型均有所提高，以第9振型为例，比板单元模型竖向振动周期提高48.9%；(4)考虑边界刚度的不利影响，钢楼梯结构竖向自振周期小于0.333 s，满足相关设计规范的要求[11-12]。

4 结语

(1)对置于楼面跨度较大的楼梯结构，楼面刚度对楼梯梁内力分布影响较大，尤其是对于弯矩的影响；在不同荷载工况下，楼梯梁弯矩呈现出不同的分布特性。对于楼梯梁轴力的影响主要表现为使得斜梁段内轴力分布不再单一，出现拉压变号情况，最大轴力出现部位发生变化。

(2)楼梯结构自振周期对边界刚度敏感，振型分布与不考虑边界刚度的计算模型差异明显。

(3)考虑楼面结构边界刚度后，楼梯结构水平及竖向自振频率均有较大幅度降低，因此设计中不应忽略楼梯结构支座刚度的影响。

(4)实际工程中类似楼梯结构设计时，不应采用独立的计算模型作为计算分析的依据，建议采用与主体结构联合计算的方法，以计入边界刚度的不利影响，获得结构构件真实内力；尤其是对于竖向自振频率的计算应以联合计算模型的分析结果为依据。

[1] 郑健.铁路旅客车站细部设计[M].北京：人民交通出版社，2010.

[2] 中华人民共和国建设部.GB 50017—2003钢结构设计规范[S].北京：中国计划出版社，2003.

[3] 黄刚.昆明南火车站结构设计研究 [J].铁道标准设计，2013(6)：136-139，146.

[4] 陈政清，华旭刚.人行桥的振动与动力设计[M].北京：人民交通出版社，2006.

[5] 赵建强，朱丹晖. 烟台火车站大跨度拱架固定铰支座设计[J].铁道标准设计，2012(6)：127-131.

[6] 中华人民共和国住房和城乡建设部.GB50009—2012建筑结构荷载规范[S].北京：中国建筑工业出版社，2012.

[7] 爱德华·L·威尔逊.结构静力与动力分析[M].原著第4版北京：中国建筑工业出版社， 2006.

[8] 楼梦麟.振动模态分析的Wilson-Ritz向量法[J].地震工程与工程振动结构，1992(11)：41-47.

[9] 包旭范，赵慧玲，袁勇，等.大跨度弧形悬吊楼梯动力特性研究[J].结构工程师，2008(7)：70-75.

[10]黄永安.西宁站站房倾斜框架柱和拱形钢桁架结构设计研究 [J].铁道标准设计，2014(6)：150-152.

[11]中华人民共和国住房和城乡建设部.GB50010—2010混凝土结构设计规范[S].北京：中国建筑工业出版社，2010.

[12]北京市市政工程研究院.CJJ 69—95城市人行天桥与人行地道技术规范[S].北京：中国建筑工业出版社，1996.

The Design of Steel Structure Stairs with Elastic Boundary Conditions in Xining Station on Lan～Xin Railway Line

ZHANG Ya-juan

(China Railway First Survey & Design Institute Group Ltd.， Xi’an 710043， China)

In view of the present big railway stations with large span steel staircase structures， which are compared and analyzed by means of independent calculation model and combined station building calculation model， this paper reveals the differences in internal bar stress and self-vibration characteristics of the staircase structure under complicated boundary conditions. The results show that the bearing stiffness of stair poses significantly influence on the internal force and the self-vibration characteristics of the structure， which is one of the important factors in structural design. Meanwhile， it is suggested that similar project staircase structure design should employ combithe main structure of conjoint analysis method， in order to obtain the stair structure mechanics response of the real complicated boundary conditions.

Railway passager Station; Stair structure; Independent analysis; Conjoint analysis; Natural vibration period; Eigenvalue analysis; Ritz vector method

2014-06-16；

2014-06-23

张亚娟(1982—)，女，工程师，2005年毕业于长安大学土木

工程专业，工学学士，E-mail:22615084@qq.com。

1004-2954(2015)03-0134-04

TU74

A

10.13238/j.issn.1004-2954.2015.03.032