Akima插值法在凸轮加工中的应用
2015-11-23中航工业空空导弹研究院河南洛阳471003
■中航工业空空导弹研究院 (河南洛阳 471003)
袁维涛 刘仁春
凸轮是工程中用于实现机械化和自动化的一种主要驱动和控制机构的重要组成部分。凸轮的型线对凸轮机构的动力学性能、接触应力、润滑特性有重要的影响。因此,凸轮的特征曲线往往由复杂的曲线构成。由于凸轮具有形状复杂、加工精度要求高等特点,一直是制造加工的难点之一。在实际生产加工中,往往不知道精确的凸轮轮廓线方程,只能得到一些离散点。
如何按这些离散点加工出“光滑”的轮廓,国内的华中科技大学和北京机械工业学院等一批科研单位也在从事这方面的研究,认为数控系统是研究高性能凸轮加工的关键技术,由它完成数控加工的复杂计算和控制。一般的数控系统只有直线和圆弧插补功能,对于凸轮这种列表曲线加工程序的编制,要离线在计算机上对列表曲线进行拟合、插值,其实在C A D软件中的样条曲线也是用某一种插值算法完成画图的。然后编制微小直线段逼近。这不仅导致编程复杂,效率低,代码量大,而且加工精度低,进给速度受限,很难满足高速高精度的数控加工要求。应当开发具有不规则曲线处理功能的数控系统,提高数控系统的数据处理能力。由数控系统进行等速度高精度插补,保持切削力平稳,才能加工高性能的凸轮。因此,提高凸轮的加工精度和加工效率,研制凸轮高精度的插值算法至关重要。
1. 插值原理
插值问题就是在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点,并估算出函数在其他点处的近似值。即假定区间[a,b]上的实值函数f(x)在该区间上n+1个互不相同点x0,x1……xn处的值是f [x0],……f(xn),要求估算f(x)在[a,b]中某点的值。
最常用的曲线的插值方法有:线性插值、Akima插值、三次样条插值等,下面以Akima插值法为例,分析如何在数控系统中用高级宏程序实现数控编程加工。
Akima插值:即设已知数据点位(xi,yi)(i=1,2,3,4,n),现在要找到一条光滑曲线y=f(x),使得满足yi=f(xi)。所谓“光滑”,是指f(x)具有连续的一阶导数。同时还约定,在任意两相邻的数据点之间,用三次多项式来逼近。即

由此可知,确定每一个数据点上的导数就是一个关键的问题。所以必须取6个连续点坐标,设用i(i=1,2,3,4,5,6),插值点(x,y)位于第三和第四个坐标点之间,经把上式推导可得
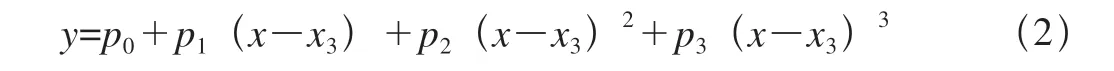
其中

上述t3,t4分别是第三和第四坐标点的斜率,他们分别用1,2,3,4,5和2,3,4,5,6点的指标值计算,即下式

式中i=3,4。mi为斜率,它用下式计算
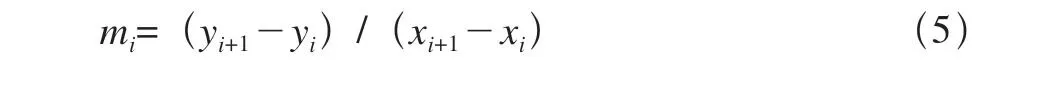
由于式(4)的分母不能为零,所以在这种情况下Akima规定:ti=(mi-1+mi)/2或ti=mi。根据以上5个公式可以用高级宏程序编制成数控加工程序。
Akima插值法在数控编程中只用到点坐标,不需要另外提供一阶导数等其他条件,显然该插值法更符合数控加工要求、更适合数控系统。并且在满足精度要求的情况下,相对简单,易于编程,调试,具有独到的优点(见图1)。下面是根据给定的凸轮坐标点,用Akima插值法编制的数控加工程序。
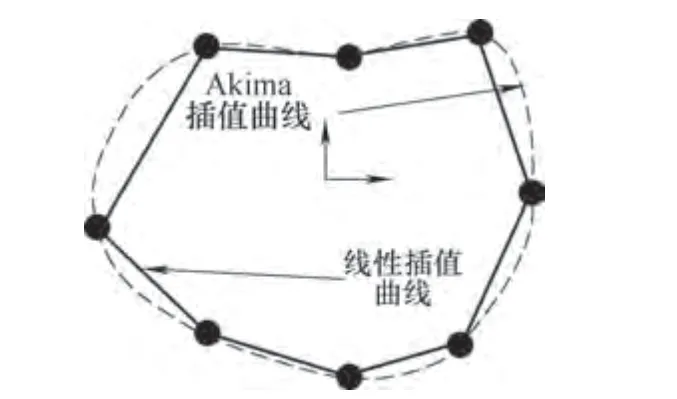
图 1
2. 程序实现
给各个坐标点初始化赋值,#101=46.497,#151=0.000……#149=43.957,#199=19.571。程序如下:
G54G00Z300M03S1000F500
G01X0Y0Z148
#1=3
WHILE [#1LE[45+3]]DO2
(根据推导公式循环计算变量值)
#11=#[100+#1-2]
…
#26=#[150+#1+3]
#17=[#[150+#1+1-2]-#[150+#1-2]]/[#[100+#1+1-2]-#[100+#1-2]]
#18=[#[150+#1+1-1]-#[150+#1-1]]/[#[100+#1+1-1]-#[100+#1-1]]
#19=[#[150+#1+1-0]-#[150+#1]]/[#[100+#1+1-0]-#[100+#1]]
#20=[#[150+#1+1+1]-#[150+#1+1]]/[#[100+#1+1+1]-#[100+#1+1]]
#21=[#[150+#1+1+2]-#[150+#1+2]]/[#[100+#1+1+2]-#[100+#1+2]]
#23=[ABS[#20-#19]*#18+ABS[#18-#17]*#19]/[ABS[#20-#19]+ABS[#18-#17]]
# 2 4 = [ A B S [ # 2 1 -
#2 0]*#1 9+A B S[#1 9-#1 8]*#2 0]/[ABS[#21-#20]+ABS[#19-#18]]
IF[[ABS[#20-#19]+ABS[#18-#17]]NE0] GOTO23
#23=#19
N 2 3 I F [ [ A B S [ # 2 1 -#20]+ABS[#19-#18]]NE0] GOTO24
#24=#20
N24 #30=#[150+#1]
#31=#23
#32=[3*[#[150+#1+1]-#[150+#1]]/[#[100+#1+1]-#[100+#1]]-2*#23-#24]/[#[100+#1+1]-#[100+#1]]
#33=[-2*[#[150+#1+1]-#[150+#1]]/[#[100+#1+1]-#[100+#1]]+#23+#24]/[[#[100+#1+1]-#[100+#1]]*[#[100+#1+1]-#[100+#1]]]
#7=[#[100+#1+1]-#[100+#1]]/5
#5=#[100+#1]+1*#7
# 6 = # 3 0 + # 3 1 * [ # 5 -#[100+#1]]+#32*[#5-#[100+#1]]*[#5-#[100+#1]]+#33*[#5-#[100+#1]]*[#5-#[100+#1]]*[#5-#[100+#1]]
G01X#5Y#6Z153
…
#1=#1+1
END2
G00Z300
M30
3. 数控程序验证
通过在MAZATROL小巨人加工中心(见图2),加工验证,用没经过处理的原始数据加工的凸轮轮廓,在曲率变化大的地方,与理想的轮廓曲线“偏离”最大。而用经过Akima插值处理过的公式曲线加工的凸轮轮廓非常“光滑”(见图3)。

图 2

图 3
4. 结语
可见凸轮的数控加工条件比较复杂,凸轮型值点的数据处理对凸轮的型面精度影响较大。为了加工出更“光滑”的凸轮型面,本文用插值法完成数据处理,并以Akima插值法为例在数控系统中用高级宏程序实现数控编程应用,并取得良好的效果。
[1] 杨大地,王开荣编著. 数值分析[M]. 北京:科学出版社,2006.
[2] 聂桂根,万剑华. Akima插值法在测量中的应用[J]. 测绘科学,1998(3).
[3] 邵才瑞. 井筒数据的Akima插值重采样方法[J]. 测井技术,2004,28(2).
