借助几何图形解代数型问题举例

覃礼权

（贵州省沿河县客田中学 贵州沿河 565300）

借助几何图形解代数型问题举例

覃礼权

（贵州省沿河县客田中学 贵州沿河 565300）

数与形有着紧密的联系，在一定条件下它们可以相互转化，因此面对特殊的代数问题，可以将已知条件与几何图形建立联系，把条件中的数量关系寓于特定的几何图形之中，就能迅速、准确地找到解题途径。

几何图形 代数 数形结合 举例

有些特殊的代数问题，已知条件中的数量关系蕴含着一定的几何背景，具有明显的几何意义。如果我们将已知条件与几何图形建立联系，把条件中的数量关系寓于特定的几何图形之中，常常能迅速、准确地找到解题途径。下面举例说明。［1］

例1、若正实数x、y、z、r满足条件

求证：xy=zr。

分析：如图1，由条件⑴式可以构造直角三角形ABC，使AC=y，BC=x，AB=z，由条件⑵式联想，作斜边上的高CD，则CD=r，借助三角形面积并可以证明。

证明：在Rt△ABC中

（图1）

分析：构造如图2所示的几何图形，其中AC⊥CD，BD⊥CD，AC=4， BD=3，PC=x，PD=y，则即a=AP+BP。作点B关于直线CD的对称点F，连结AF，a的最小值为线段AF的长，作矩形CDFE，并可以求解。

在Rt△AEF中，AE=7，EF=6，由勾股定理得［2］

（图2）

分析：如果用我们生活中的一些基本常识来解本题，是显而易见的。例如，b克糖水中，内含a克糖，糖的质量分数为若再往糖水中加入m克糖，糖的质量分数就变为了糖水比开始也更甜一些。这表明

实际上，这个问题的结论我们还可以借助几何图形得出。

解：如图3所示，由于0＜a＜b，所以S+S1＞S+S2

即ab+bm＞ab+am

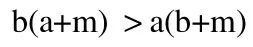
不等式两边同时除以正数b（b+m），得

（图3）

例4、试比较x2与 x|的大小。

分析：直接比较x2与 x|的大小不方便。如图5，如果我们分别作出函数y=x2与函数y= x|的图象，借助二图像，很容易求解。［3］

解：如图4所示，分别作出函数y=x2与函数y= x|的图象。求出二图象交点的横坐标xA=-1，xB=1，xo=0

由图象可知，

当x＜-1或x＞1时，

当-1＜x＜0时，

当x=±1或x=0时，

（图4）

我们看到，以上例子都是利用了“数形结合”的思想。实际上，形与数是数学的两大支柱数。数借形有直观作用，而形借助于数可以找到内在规律。它们之间是没有鸿沟的，也不是相割裂的，而是相辅相成、互相转化的。学会用“数形结合”的思想分析和解决问题，就是要实现由数思形，以形助数，适时转化、相互为用。

［1］李明，张锐.构造几何图形解决代数问题［J］.数学教学研究，2012，31（2）：67-67.

［2］董彪.浅议利用几何图形解决代数问题［J］.阿坝师范高等专科学校学报，2003，（1）：101-104.

［3］韦国友.巧构几何图形妙解代数问题 ［J］.中学生数学，2013，（20）：17-17.