基于数控程序重构的加工中心误差软件补偿技术
2015-11-22胡世军王恩广侯剑波陈玉荣
□ 胡世军 □ 刘 学 □ 王恩广 □ 侯剑波 □ 陈玉荣
兰州理工大学 机电工程学院 兰州 730050
基于数控程序重构的加工中心误差软件补偿技术
□ 胡世军 □ 刘 学 □ 王恩广 □ 侯剑波 □ 陈玉荣
兰州理工大学 机电工程学院 兰州 730050
论述了基于数控程序重构的机床软件补偿技术的原理,提出了无限插值定位确定误差补偿点的方法,克服了等间距确定误差补偿点法在间距内误差无法控制的缺陷;研究了数控机床三种基本编程运动的数控程序重构算法;分析了反向间隙的补偿;在FANUC Series 0i Mate-MC操作系统的VMC-860型三轴立式加工中心进行补偿实验,得出该补偿技术能使数控机床的几何误差减少50%。
数控程序重构 无限插值定位 软件补偿
随着计算机技术和测量技术的发展,机床误差软件补偿技术日趋成熟。数控机床软件补偿技术研究的内容包括数控机床误差模型的建立、误差的参数测量和辨识以及误差补偿方法研究[1]。目前常用的误差补偿方法是通过建立的误差模型修改数控程序,即数控程序重构。数控程序重构为软件补偿中非常重要的一环,其核心为误差补偿点的确定和基本运动的误差补偿算法。目前国内外采用的是等间距确定误差补偿点的方法,补偿间距为预设的一个常数,存在间距内的误差无法控制的缺陷[2]。本研究给出了一种能无限插值定位划分误差模型来确定补偿点的方法,使机床的误差补偿有很大的柔性。
1 软件补偿原理
数控机床的基本功能是按照数控加工程序,使切削刀具与被切削工件之间实现准确定位和相对运动。首先需要建立理想指令与实际运动之间的误差模型,然后将误差值按照一定的计算方法反向叠加到 数控系统的插补指令上,使误差部分抵消,实现误差补偿[3]。
用多体系统理论建立误差模型,使用9线位移误差及直线度误差测量辨识数控机床整个工作区间内的全部21项几何误差参数,得出刀具理想运动轨迹和实际运动轨迹之间的误差值E(x,y,z)[4]。
假设理想刀具轨迹上任意一点P的坐标为(x,y,z),该点对应的误差为ep,将该点误差分解到X、Y、Z轴上,得ex(P)、ey(P)、ez(P)。补偿前刀具实际到达点Pa(xa,ya,za),则:

补偿后刀具期望到达点Pc(xc,yc,zc),则:

补偿后刀具实际到达点Pac(xac,yac,zac),则:

从上式可以看出,补偿后实际到达的点Pac,相对于理想的轨迹点P依然存在误差e(Pc),但是相对补偿前轨迹点Pa已有很大的改善。
2 数控程序重构的实现
2.1 误差补偿点的确定
本研究采用无限插值定位确定误差补偿点的方法,如图1所示,以X轴的误差曲线为例,水平分割误差曲线ex,当误差值累计达到预设的偏差ε时,在该处设定一个补偿点。在确定第一个补偿点x1并对其进行补偿之后,理论上误差ex回到零点,到累计误差达到2ε时,确定第二个补偿点x2,x1与x2之间的误差曲线平移到图中的曲线1,可见x1与x2之间各点的误差小于ε。依次类推,在ex=nε(n为常数)处设立补偿点,当误差反方向发展时,如从x4到x6,只需将误差值由正值变为负值代入补偿公式,补偿点的确定依然满足ex= nε,此时n为负数。
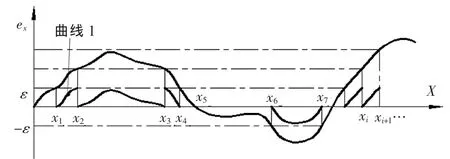
▲图1 X轴的线性位移误差
2.2 基本运动误差补偿算法
基本编程运动有3种:快速定位、直线插补、圆弧插补[5]。
2.2.1 快速定位的补偿算法
设刀具运动的目标点为P,实际到达点为Pan,补偿后的点为Pcn,其中n为补偿次数,当n=0时,Pc0=P,由误差模型计算出该处的误差为e(P),则:

当e(P)<ε,不补偿;当e(P)≥ε,进行第一次补偿,得:

理论上补偿后刀具已到达目标点P,而实际补偿运动同样会产生误差,通过误差模型计算出第一次补偿后点Pc1处的误差为e(P1),此时刀具实际到达的点Pa1,则:

第一次补偿后的残差e1′=Pa1-P,由上式得 e1′=e(P1)-e(P)。当e1′<ε,补偿终止;当e1′≥ε,进行第二次补偿,得:

当e2′<ε,补偿终止;当e2′≥ε,重复以上计算进行第三次补偿,直到残差小于ε为止,由传递运算得出第n次补偿后为:

2.2.2 直线插补补偿算法
直线插补运动用来使刀具由当前位置移动到目标位置,对刀具的切削轨迹有线性要求。直线插补运动的误差补偿,采用无限插值定位划分误差模型来确定补偿点[6]。
假设刀具切削点P沿着Pq、Pz之间运动,将直线PqPz在对应的X、Y、Z轴上等间距划分,可得从起点沿着刀具运动方向第n点的坐标为:

式中:dx、dy、dz分别为刀具沿X、Y、Z三个运动轴上的递增量,其值可正可负。
判断,当n=0时,即为起点Pq的误差是否超出精度控制ε,从误差模型中提取Pa点X、Y、Z坐标轴上对应的误差ex(Pq)、ey(Pq)、ez(Pq)。若,且时,该点不补偿,直接进入下一点的判断。只要某一轴,则需要对该轴进行补偿, 其余轴不补偿。 若,且时,对X轴进行补偿,第一次补偿后期望到达的目标点为Pc01,则:

根据式Pa1=Pc1+e(P1)、e1′=Pa1-P进行补偿判断,当ex1′<ε时,不补偿,当ex1′≥ε,进行第2次补偿,直至第n次补偿后,exn′<ε停止补偿,进入下一个点。当n=1时,判断P1点误差与精度控制ε之间的关系,不需要补偿进入下一点;需要补偿,用上式进行补偿。按上述方法递归循环,直至到达终点Pz。
2.2.3 圆弧插补补偿算法
圆弧插补补偿算法与直线插补类似,与之不同的是采用与插补弧线半径之差为ε的同心弧线控制精度,采用无限插值定位分割弧线误差模型来确定补偿点。
如图2所示,以XOY平面内顺时针圆弧PqMPz作为研究对象,将圆弧M按等角度间距dθ划分,设圆弧上第n个划分点为Pn(xn,yn,zn),则:


▲图2 圆弧插补运动误差补偿点确定示意图
式中:xh、yh为圆心对应在X、Y轴上的坐标;r为半径;θq圆弧起点Pq与过圆心X轴正方向的顺时针夹角。
首先判断,当n=0,即起点Pq,从误差补偿模型中调取该点的ex(Pq)、ey(Pq)判断是否超出精度控制ε,若,该点不补偿,直接进入下一点的判断。若只要某一轴e(Pq)≥ε,则需要对该轴进行补偿,假设此时,则:

然后根据式Pa1=Pc1+e(P1)、e1′=Pa1-P进行补偿判断,当ex1′<ε时,不补偿。当ex1′≥ε,进行下一次补偿,直至第n次补偿后,exn′<ε停止补偿。在圆弧补偿中需要特别注意,圆弧补偿后,圆心坐标也随之改变,因此,对于采用终点圆心的编程方式,需要确定补偿后的半径rc。假设该点通过一次补偿即满足条件,得补偿后点Pcq(xc01,yc02),则:

当 n=1,判断第一个分段点 P1误差与精度控制ε之间的关系,不需要补偿,进入下一点,需要补偿,用上式进行补偿。按上述方法递归循环,直至到达终点Pz。
2.3 反向间隙补偿
数控机床在加工中经常换向,因而误差补偿有正反向之分[6]。 如图3,图中e1为正向的误差曲线,e2为反向的误差曲线。经正向补偿后,反向误差曲线e2变成e′,e′也称为反向间隙曲线,主要由机床传动机构的间隙造成[6]。以X轴运动为例,当机床正向插补运动到点xi进行反向插补时,下一周期实际的运动距离为:

▲图3 反向误差补偿

式中:ei+1=ei′=e2i-e1i。
是否进行换向插补,由指令值的正负号决定。
3 机床误差软件补偿实例

▲图4 加工试件的几何结构
为了验证软件补偿方法的正确性,采用FANUC Series 0i Mate-MC操作系统的VMC-860型三轴立式加工中心进行试切实验。实验前用激光干涉仪测量识别机床的误差参数,并将相应的参数文件输入补偿软件,然后通过软件计算得到重构程序,用重构程序加工试件2,用补偿前程序加工的试件1,图4为试件1、2的几何结构。利用三坐标测量仪测量加工得到试件1、2相应的参数,如表1。
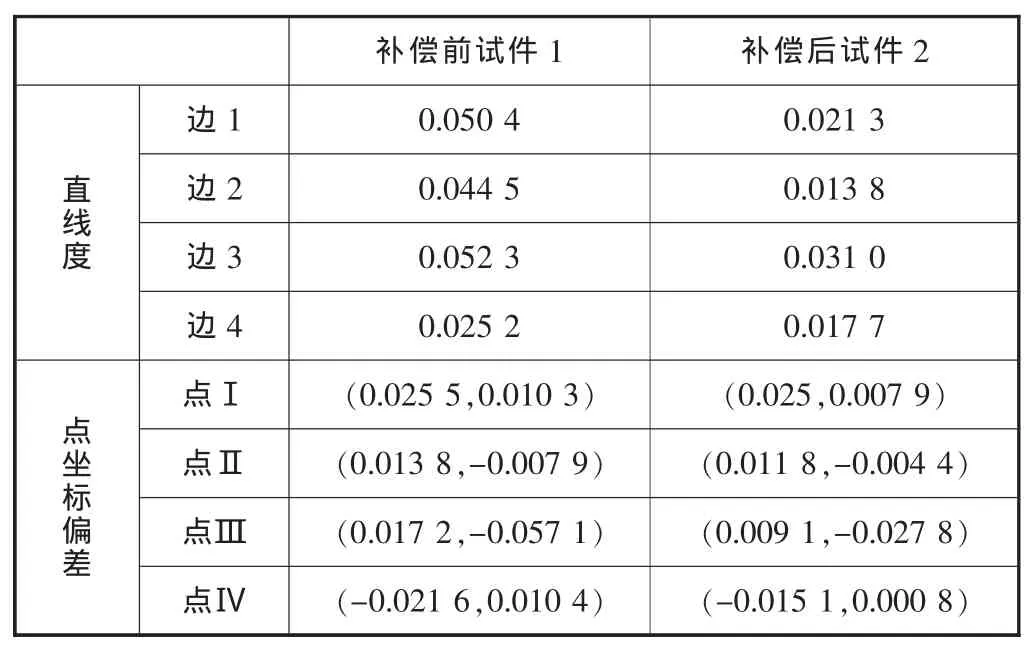
表1 两组工件的相关参数比较/mm
由表1可知,补偿后试件的直线度和点坐标的偏差明显减小,基于数控程序重构的对加工中心进行软件补偿的方法,可以有效减少机床的几何误差,提高机床的加工精度。
4 结论
从上述的补偿试验结果可以得出以下结论。
(1)本文提出的基于数控程序重构的误差补偿方法切实可行。
(2)采用无限插值定位确定误差补偿点方法能有效减少补偿程序的数量,且能很好地将机床精度控制在一个预设偏差中。
(3)本文提出的误差补偿方法特别适合提高老旧机床的加工精度。
[1]刘又午,刘丽冰,赵小松,等.数控机床误差补偿技术研究[J].中国机械工程,1998,9(12):48-52.
[2]张虎,周云飞,唐小琦,等.数控机床定位误差的软件补偿[J].华中科技大学学报,2001,10(1):47-49.
[3]张虎,周云飞,唐小琦,等.多轴数控机床的软件补偿技术[J].机械工程学报,2001,37(11):58-61.
[4]唐笑.三轴数控铣床几何误差补偿技术研究[D].南京:南京航空航天大学,2009.
[5]韩建海.数控技术及装备 [M].武汉:华中科技大学出版社,2007.
[6]冯国元.数控车床的几何误差软件补偿[D].武汉:华中科技大学,2002.
(编辑 小 前)
TH161;TG659
A
1000-4998(2015)04-0079-03
2014年10月
