考虑碳排放的多目标发电优化模型

刘思东 任海斌

（五邑大学数学与计算科学学院，广东 江门 529020）

考虑碳排放的多目标发电优化模型

刘思东 任海斌

（五邑大学数学与计算科学学院，广东 江门 529020）

近年来，控制二氧化碳的排放量一直是我国保护环境的重要措施。发电厂为了控制二氧化碳的排放量，就必须根据各时段出力的不同，重新调整自己的发电计划，对发电计划进行优化，控制二氧化碳的排放响。文章通过对发电所需的成本，所得的利润等情况，考虑发电机组自身的不同参数值，建立多目标优化模型。借助仿真实验，利用lingo软件对多目标优化模型进行求解，求出每个机组每个时刻的最佳出力和运作状态，得到发电的最优计划。

多目标优化；非线性模型；碳排放；lingo

1 引言

缓解全球气候变暖，保护自然环境，应对气温上升的气候问题，为我们的未来作贡献，我国必须对火力发电厂在火力发电的过程采取相应措施，以控制发电产生的二氧化碳的排放量，企业必须通过研究合理的发电计划来控制二氧化碳的排放量[1]。

企业为了自身能获得更多的利润，大量发电，而大量发电所带来的负面影响，就是矿物质燃料燃烧排放出大量的二氧化碳，同时由于发电量过大，电储存量过多，无法消耗的电量也会造成不必要的浪费。

另一方面，由于大量发电，存储电量远大于所需要的发电量，首先带来的是发电成本的增加。因为每一单位的燃料可以产生的电量是基本固定的，所以大量发电就必须要提供大量的燃料，燃料的增加自然就会使得成本的增加。其次由于发电量过大，电储存量过多，无法消耗的电量会由于没有出售而得不到利润，而企业为了填补这笔没有出售的电量的成本，会把平均电价提高，以损害普通市民利益的形式来保证自己的收益。

总而言之，研究如何能更好地安排发电计划，对我国控制二氧化碳的排放量起主导性作用。但是，在火力发电厂中存在着不同型号的发电机组，而每个不同的发电机组的各项参数也不尽相同，在考虑极限输出影响的前提下，如何使火力发电厂在尽可能少地排放二氧化碳的同时，获得更多的利益，是急切等待解决的问题，因此，对于各时刻的安排必须要进行详细规划。

2 考虑碳排放的多目标发电优化数学模型

2.1目标函数

在计算多目标优化碳排放的发电模型时，其目标函数除了发电机组发电时排放二氧化碳量最小化，还要求发电厂利润最大化。

（1）发电机组排放的二氧化碳量最小化，是该论文的主要研究目标。在这里我们根据每小时发电机组排放的二氧化碳量进行统计计算。

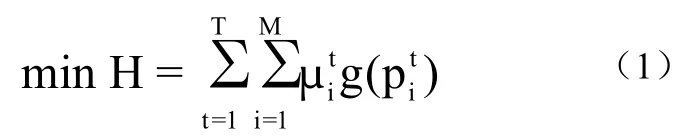
公式中：T为计算时段总数；M为用于计算的火力发电机组总台数，μi为第i个机组在第t时段的工作状态，当μi=1时，表示为第i个发电机组处于运行状态，当μi=0时，表示为第i个发电机组处于休息状态；pi为第t时段第i个发电机组火力发电的输出功率；gi(pit)为在第t时段第i个发电机组因火力发电排放的二氧化碳量。

火力发电的燃料是燃煤、焦碳等混合燃料，但燃烧产生二氧化碳的并不是全部，而是燃料中的碳元素。从化学理论上来讲，lmol碳燃烧，排放的二氧化碳的量即为碳元素碳和空气中的氧气发生化学反应后的产物。根据化学反应式，可以得到每一单位的碳元素，经过化学反应，可以得到一单位的二氧化碳。因此，在计算火力发电的二氧化碳排放量，我们就必须先求出燃料中碳元素的含有量，再根据摩尔公式、离子架构等转换推算出二氧化碳的排放量。

但从火力发电厂实际运行状态来看，燃料的元素含量比较多，分析比较复杂，如果要计算二氧化碳的排放量，那么火力发电厂在每次把燃料放入燃烧锅炉前都要进行额外燃料元素分析工作，不仅会增加火力发电厂成本与工人工作负担，同时会造成不必要的浪费。因此，在这里把二氧化碳的排放量看成跟发电量存在二次函数关系的变量，用二次函数表示为：

公式中αi,βi,γi分别为机组设定参数。

（2）发电厂利润最大化，其主要包括两部分：第一部分为上网电量收入，第二部分由发电变动成本和固定成本构成。变动成本是指随发电量增加减少而正比例增加减少的费用，固定成本是指不会因发电量增加减少而产生浮动的费用，包括机组材料费、机组维修费、机组折旧、工人工资等。由于固定成本与碳排放无直接或间接关系，在多目标优化中影响几乎为零，故在此也不对其进行考虑计算。

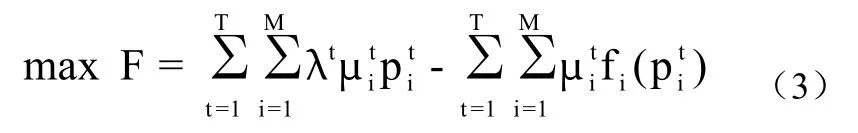
公式中：F为利润；λt为第 时段电价；fi(pit)为第i个机组在第 时段的燃煤耗量，在这里我们把发电的燃煤耗量看成跟发电量存在二次函数关系的变量，可以用二次函数式表示，用二次函数表示为：

公式中ai,bi,ci分别为机组参数。

由上面综合可得，该优化模型的目标函数为：

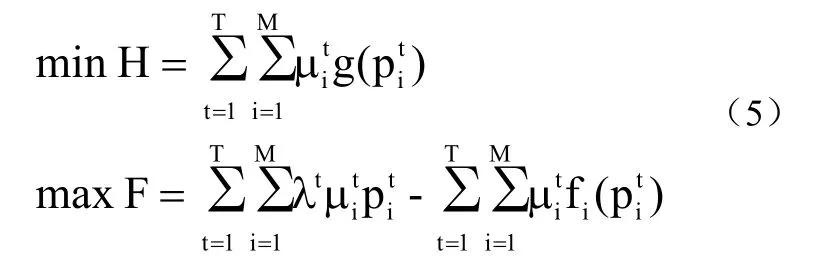
2.2约束函数

考虑到不同发电机组在优化排放二氧化碳问题会有所差别，所以在计算多目标优化碳排放的发电模型的约束条件包括以下几点：

（1）发电机组总发电负荷约束：为了保证发电机组在整个发电过程中不会因为过载而产生机械设备的损坏，需要每一时刻都对发电机组的总发电负荷进行约束，以保证总负荷不会超出限定总负荷。

（2）单个发电机组某时间输出功率约束：每个发电机组在制造时都有限定自己的最大功率，所以发电机组在运作时，其输出功率都不能大于自身的最大功率，但也不能少于一定功率。

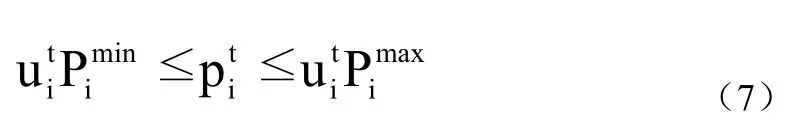
（3）发电机组爬坡约束：在考虑到发电机组运作时，发电机组会因为调节发电功率，增加或减少单位时间跨度内的发电负荷。为了保证生产安全与机组组合生产的稳定性，一般会对发电机组设置爬坡约束，单位时间内每个发电机组调节的发电功率不能超过自身的安全值。

增加单位时间内的机组负荷：

减少单位时间内的机组负荷：

公式中，ptD为第t时刻所有计算的发电机组预测负荷上限；pimin为第i个机组的最小输出功率；pimax为第i个机组的最大输出功率；RUi为第i个机组增加负荷时的爬坡约束；RDi为第i个机组减少负荷时的爬坡约束。

综合上面的公式，该模型的约束函数为：

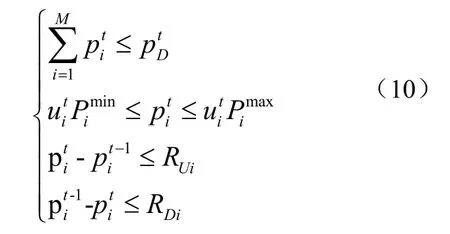
3 多目标发电优化模型的层次求解算法

层次算法求解目标规划是按照从最高层到最底层规划的原则进行规划，它的求解过程是先对目标函数的最高层进行规划，求出此层可能出现的最优解，接着进入下一层再次进行规划，重复多次，直到最后对最底层进行规划，求出最优解。

层次算法求解目标规划要注意，下一层次规划时应该在前面各层次规划的基础上进行要求。

在多目标规划过程中，目标函数并不一定是唯一的, 可能存在多条目标函数。而且目标函数与约束条件是否为线性函数也不是唯一的，一个多目标规划问题可能具有多个决策变量和多个目标变量，多目标规划问题可表述为：

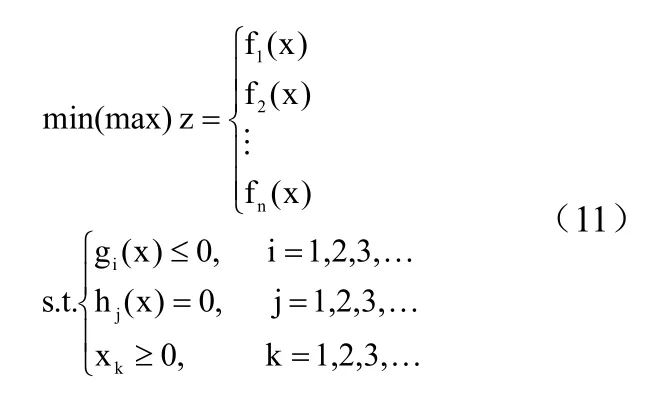
在多目标规划的求解过程中，本文采用lingo软件进行求解。具体步骤如下[2]：

（1）选择计算变量。求解多目标规划模型过程中，首先要确定求解的未知量。这些未知量一般可以表示成一组数据，未知量可能为常数，也可能为变量。变量的选取是在求解模型过程中不断进行变化与优化，可以称为设计变量，可用一个x向量x=(x1,x2,…,xn)表示。

（2）确立目标函数。理想的目标函数由决策因子的数学函数或目标函数表达，目标函数表示实现或解决某种问题的意愿，其表达式可能是非线性的，也可能是线性的。目标函数是为了实现理想目标，使之与取值范围互相配合，构成的某些决策变量的数学函数。

（3）建立约束条件。约束条件跟目标函数的表达形式相似，只是在求解模型时，为了限制或减少出现不同的结果，要求整个模型必须满足的条件。约束条件就是为实现目标函数，对目标函数的范围进行压缩，进而限制目标函数，称为约束条件。

（4）确定数学模型。当我们使用lingo软件求解多目标规划模型时，要求模型最终实现的理想目标只有一个，因此，除了最终理想目标，其他的理想目标需要根据最终理想目标所需满足的优先次序，转换成下一级的目标函数或者变成约束条件加入模型进行计算，分层次进行求解。

4 算例分析

本论文选取7个不同种类的发电机组，其机组数据如表1所示[3]，本论文通过对 7个机组分别不同时间段发电所得收入，考虑发电机组在何时进行发电生产最好。

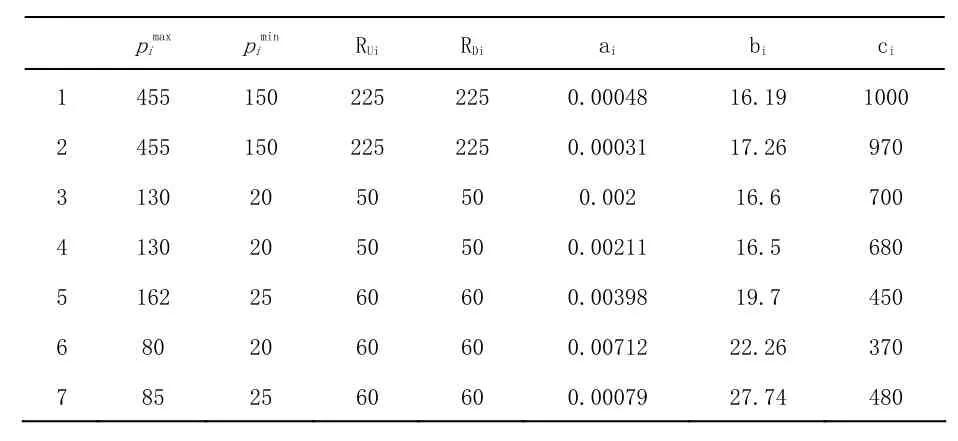
表1　发电机组相关数据参数

从表 1不难发现，在不同的常规机组中，它们的最大、最小输出功率各不相同，爬坡速度也不同，即使最大、最小输出功率与爬坡速度相同，它们的发电成本也不一定相同。

不同时段对发电厂的发电负荷都有限定要求，各时段的要求如下表。

表2　各个时段的总负荷

可以发现在9～14时刻和19～21时刻为高峰期，这些时间段内发电的总负荷比其他时间段的总负荷高，也就是说，这些时间段对电量的需求比其他时间段的需求大。

根据现在工业生产发展模式，不同时间段的总负荷有所不同，不同时间段的电量售价也不相同。一般情况下，用电高峰期期间电价会比低峰期的电价高，不同时段的电价如下表[4]。

表3　各个时段的电价

从表3中，可以发现在10～20时刻销售电价比其他时刻的售价高，也就是说，这些时间段销售同样量的电量，获得的收入比其他时间段多。

由于每个发电机组的机组参数各不相同，所以每个发电机组在每一时刻内发电所排放的二氧化碳的多少也不相同，因此我们可以根据各机组的二氧化碳排放量的排放系数来计算火力发电的二氧化碳排放量。各个机组的二氧化碳排放量的排放系数如下表[5]。

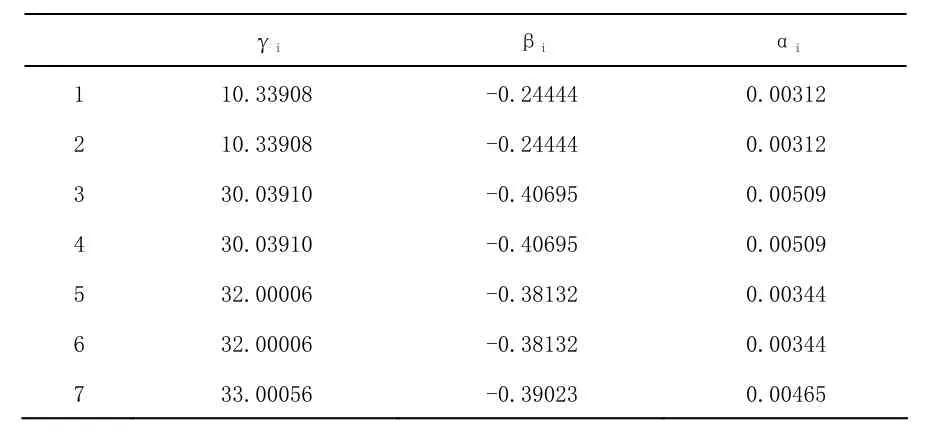
表4　机组二氧化碳排放系数

从以上数据可以看出，它们的二氧化碳排放系数也不相同，即使最大、最小输出功率与爬坡速度相同的，它们的排放系数也不一定相同。

通过lingo计算，可以得到各个时段的输出功率最优解。每个时段的实际输出功率如下表。

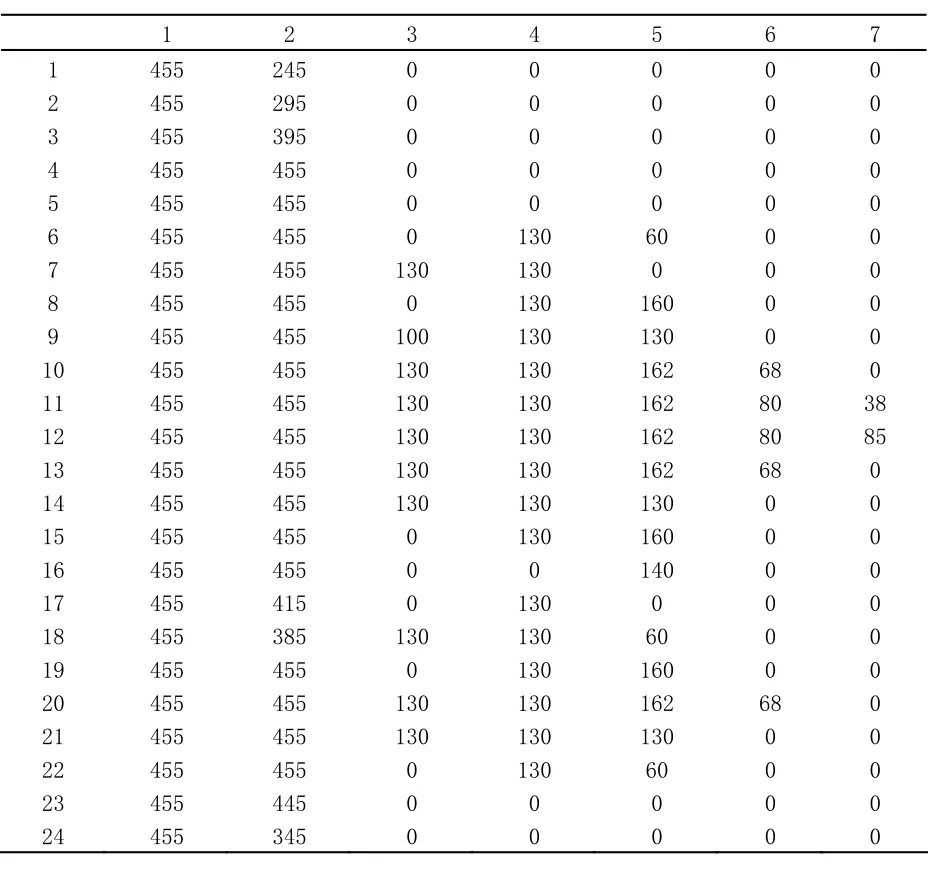
表5　7台机组24时段的最优输出功率

由表5可以看出，机组1和机组2在整天24小时内没有停止运作；机组6、机组7经常处于停机状态，除了用电最高峰时才运作；机组3、机组4、机组5经常处于运作状态，轮流合作发电。

小结以上数据，可以得到一个lingo的最优的结果。但很明显的，在这个最优化中，忽略了一些其他因素的影响，例如发电机组的损耗。从计算的最优结果来看，此时收入为1263759.0美元，成本为539443.6美元，此时利润为724315.4美元，碳排放量为27189.39ton。

从上面的表格数据来看，大功率的发电机组发电性能比较好，一般情况下，大功率的发电机组都会满功率运作，而小功率的发电机组由于效益不佳，一般不运作，以减少不必要的浪费，进一步控制成本的消耗与二氧化碳的排放量，得到目标函数最优值。

5 结论

本文主要通过对火力发电机组组合优化的研究，以二氧化碳排放量最小和利润最大为目标函数，以 7个实验机组为实例，建立了机组组合问题的优化数学模型，利用lingo程序对模型进行优化求解，通过对不同型号机组进行计算，得到计划的最优解，预测最有可能的计划。将不同的数据进行记录、对比和分析，可以得出以下这些结论：

（1）一般情况下，大功率输出的发电机组运作时间都会比小功率输出的发电机组运作时间长，输出功率越大的发电机组运作时间越长，而且输出功率基本为最大输出功率，输出功率越小的发电机组运作时间越短，输出功率主要是根据当下时刻最大限度功率输出的。

（2）同样输出功率的发电机组在发电选择时，会选择同功率下二氧化碳排放量和生产成本最小的发电机组，让这个发电机组优先生产更多的电。

[1] MENG Xiangping, GAO Yan. Electric systems analysis [M].Beijing: Higher Education Press,2004.

[2] 陈其胜,陈寿芬,农韦健,等.电解二氧化锰生产中的污水处理技术方案[J].大众科技,2013,15(1):47-48.

[1] 朱松丽.中国二氧化碳排放数据比较分析[J].气候变化研究进展,2013,9(4):265-273.

[2] 吴友平,刘杰,何杰.多目标规划的 LINGO求解法[J].湖南工业大学学报,2012,26(3):9-12.

[3] SENJYU T,SHIMABUKURO K,UEZATO K,et al.A fast technique for unit commitment problem by extended priority list[J].IEEE Trans. on Power Systems,2003,18(2): 882-888.

[4] LI T,SHAHIDEHPOUR M.Price-based unit commitment:a case of Lagrangian relaxation versus mixed integer programming[J]. IEEE Trans. on Power Systems,2005,20(4): 2015-2025.

[5] SABER A Y,VENAYAGAMOORTHY G K.Plug-in vehicles and renewable energy sources for cost and emission reductions[J].IEEE Trans. on Industrial Electronics, 2011,58(4):1226-1238.

Multi-objective optimization power model considering carbon emission

In recent years, controlling the emission of carbon dioxide is an important measure to protect our environment in China. In order to control the emission of carbon dioxide, the power plant is necessary to re-adjust the plans, the generation scheduling optimization which be based on the time of different output, controlling the emission of carbon dioxide. In this paper, combined with the cost and profit to arrange the power of conventional unit, defining The value of different parameters of generator, to study the establishment of multi objective optimization model, through the simulation experiment, obtains the optimal power output and operation state in each unit each time, which is solved by the LINGO programs, and get the best power plan.

Multi-objective optimization; nonlinear model; carbon emissions; lingo

TM73

A

1008-1151(2015)06-0072-04

2015-05-13

江门市基础理论与科学研究类科技计划项目(江科[2014]14号)；五邑大学青年科研基金资助项目(2013zk04)。

刘思东（1982－），男，湖南平江人，五邑大学数学与计算科学学院讲师，博士，研究方向为最优化方法及其应用。