经历探究过程 深化数学思考——从一道思考题的教学说起

江苏海安县城南实验小学（226600） 刘智勇

经历探究过程 深化数学思考
——从一道思考题的教学说起

江苏海安县城南实验小学（226600） 刘智勇

在各类数学问题解决中，思考题是直接以“思考”来冠名的。要充分体现思考题的思考价值，不能只关注解题的方式和结果，更要关注研究过程，激发学生的探究需要，让学生经历探究过程，主动进行反思，以思考题的教学推动数学思考能力的培养。

思考题 过程 结果 反思

下图是学生刚刚学习三个两位数连加后的一道思考题（苏教版义务教育数学新教材二年级上册第5页）。这道题里数量多，信息量大，思维要求高，初次看到它时，我也琢磨了一会儿才形成思路，对刚刚进入二年级的学生而言，显然是有难度的。

该怎么教学呢？我请教了本年级的几位老师。有的老师说，班上总有“好”的学生能解决，请这些学生做“小老师”；有的老师说，还是等教好了后面的几道例题，让学生对两位数的加减法有了比较好的基础后再来研究这道题。我想，数学课堂应该面向全体学生，不能只是“好学生”的主场；教材在此处编排这道思考题应该是为后续教学作铺垫，如果等后面的相关知识学好了再回头教学，思考题的价值就大大削弱了。于是，我决定还是“还舞台”给学生，进行一次教学尝试。

（学生读题，同桌合作研究）

生1：我们两个人做了一下加法，左边车上30+28+ 26=84个，右边车上26+24+22=72个，两车上的苹果数不一样多。

师：通过计算，你们发现左边车上的苹果——（多），右边车上的苹果数——（少）。

生1：我们还算出左边车比右边车多12个苹果。84-72=12（个）。

师：看到数据想到计算，真会学习！既然两车上的苹果不一样多，怎么能让“两车运的苹果个数同样多”呢？

生2：从左边车上拿6个给右边车上。

师：题目中的意思是——

生3：交换筐。

师：怎么交换？

生3：我们把两车上的苹果数量整理了一下，左边车上最多的一筐是30个，右边车上最多一筐只有26个；左边车上最少的一筐是26个，右边车上最少的一筐是22个；左边车上还有一筐是28个，右边车上还有一筐是24个。把30和26换一下。

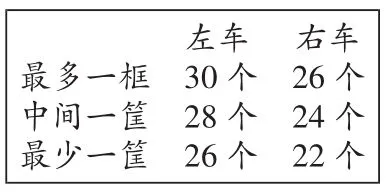
师：你们把数据整理后，题目的意思变得清楚多了。把30和26换了以后，两车运的苹果个数同样多了吗？

生3：好像不对，28和24换，26和22换也都不行。

生4：两车中都有一筐是26个，只要考虑其他的四框怎么换。

师（表现出很惊喜的样子，擦掉两个26，简化表格如右）：交换哪两筐苹果就可以使两车的苹果个数同样多？再研究一下。

生5：把30个和24个的筐换一下。左边车为24+28=52（个），右边车为30+22=52（个）。

生6：把28个和22个的筐换一下也行，左边车为30+22=52（个），右边车为24+28=52（个）。

师：如果把30个和22个的筐换一下，行不行呢？

生7：不行，这样换左边有22+28=50（个），右边有30+24=54（个），不一样多。

师：经过大家的共同努力，这道思考题终于被解决了。比较两种成功的换法，你们有什么发现？

生8：这两种换法都没有换26个。

师：为什么不让26参加换呢？

生8：两车上都有26个。

师：是啊，两边都有26个，交换的时候我们就可以不考虑。看来解决问题时，可以先排除一些无关信息，让问题解决变得简单一点。

生9：30比24多6，28也比22多6。这也是两种换法中的相同点。

师：还记得原来左边车上比右边车上多几个苹果？

生：12个。

师：你有什么发现？

生10：6是12的一半。

师：是啊，所谓换框，实际上就是换总数“12的一半”。刚才有一位同学好像说到了“6”。（伸手邀请生10起立）能说说你的想法吗？

生10：从左边车上拿6个给右边车，两车运的苹果就同样多了。

师：要是这道题中，没有提出“换框”的要求，最直接的方法就是——

生：从左边车上拿6个给右边车。

（老师带头鼓掌，教室里响起了掌声！）

教材中的思考题是大家公认的超越了一般学习难度的题目，它的难度往往体现在解题的思考过程比较复杂，思路比较特殊，解法具有独特性和开放性。思考题的教学，如果处理得好，能点燃学生的学习热情，让学生感受到数学的奇妙和精彩；如果处理得不好，会让学生产生畏难情绪，进而会害怕数学，结果与初衷相背离。上述思考题的教学案例，给了我很好的启示。

1.数学思考的基础是让所有学生的脑子都“转动”起来。低年级的数学学习因为难度不大，解决问题的步骤一般不超过两步，学生普遍“看一眼”就知道怎么办，甚至于答案脱口而出。事实上，面对稍有难度的问题，解决时不可能一步到位，首要的不是直接解题，而是梳理解决问题所具有的素材和信息，寻找数量之间的关联。这就需要让所有学生的脑子都要“转动”起来，能迈出一步迈一步，能迈出两步就迈两步，一步一步地前进，最后逼近问题解决的关键和核心。其中，最重要的就是鼓励学生积极参与，勇于展示自己的思考成果。在学生都充分展现自己的研究成果后，教学就有了很好的基础，交流和深入就有很好的依托。比如，解决上述思考题，有学生首先想到“计算”，这很正常，一是最近集中学习计算，二是有了数量就想到计算。只是纯粹的计算本身并不能解决这个问题，这就需要进一步地分析数据的特点，以及考虑计算后所得到的初步结论（左边车上比右边车上多12个）有什么可利用的价值。如果没有学生脑子的“转动”，那数学思考就成为无源之水、无本之木。

2.过程孕育结果，结果就在过程中。长期以来，人们总是对数学问题解决的结果保持着“极高的热情”，以结果判得分，以结果论对错，这也导致了关于“重结果轻过程”“重过程轻结果”“既要重过程又要重结果”的各种讨论。我认为，这些讨论都是将“过程”和“结果”分离开来看，对立起来看。事实上，过程孕育结果，结果就在过程中，过程就是我们需要的结果。这里的结果不只是问题解决的方法、过程和答案，还包含在问题解决过程中学生的主动性、互动性、生成性、发展性等。这在上述思考题的教学案例中是体现得非常充分的。从试图通过数量的直接计算来解决问题，到发现“两车上都有一筐是26个”后把问题解决的思路变得简单一点，再到借助于数感和口算能直接看出答案，层层剥笋，环环相扣，拾级而上，最终进入“豁然开朗”的境地。数学是冰冷的、抽象的，可思考是火热的，可以触摸的，经历了这样的过程，学生获得的不只是数学思考的方法，更有对数学的感受——享受到深刻的、有趣的数学学习的成功愉悦。

3.在反思中超越。反思也是一种思考，是一种对学习行为的对错、优劣、好差等更为深入的思考。通过反思，可以更好地提升思考能力，提高学习效果。在解决问题过程中，学生的个体思维存在很大的差异性，但是经过梳理、对比、讨论、交流后，彼此间的差异性就显现出来了，此时，每个学生都可以进行反思活动，不仅反思自己，还应该在散乱中寻找有序，从多样化中寻找最优化。只有经过反思，学生才会逐步建立反思意识，产生反思自觉。这种反思也应该包括教师的教学反思。例如“两车苹果相差数12”“相差数的一半是6”“拿出相差数的一半给较小数，两数量就相等”等数量关系学生在一开始的研究中似乎就有所感觉到，这出乎了老师的预料。要是顺着生10的发言，花点时间，让他解释自己的想法“从左边车上拿6个给右边车”，可能整个课堂就首尾“翻转”过来了，同时对于解决涉及“相差数”的问题，他们也会有更进一步的认识。那样，整节课的教学又是另一番景象了。

总之，教材中的思考题，我们要充分发挥它应有的价值——引导学生充分思考，经历探究过程，掌握探究方法，发展学生思维，最终达到深化数学思考的目的。

（责编 金 铃）

G623.5

A

1007-9068（2015）14-009