数学思考，需要怎样的学习素材？

浙江奉化市教师进修学校（315500） 宋煜阳

数学思考，需要怎样的学习素材？

浙江奉化市教师进修学校（315500） 宋煜阳

数学思考需要好的学习材料为载体。在设计和选择学习素材时，需要讲求数学眼光，关注情境性素材的抽象转化与直观表征；需要讲求整体感知，关注比照性素材的关系概括与类比推理；需要讲求路径习得，关注梳理性素材的方法追溯与策略提炼。

数学思考 学习素材

数学学习的本质是让学生学会数学思考，而学会数学思考，通俗地说就是学会用数学的思维方式想问题。无论是学生想问题意愿的激发，还是想问题经验方法的积累，学习素材至关重要。

那么，什么样的学习素材能触发学生的数学思考呢？笔者认为，这种素材首先需要“诱导性”，所蕴含的学习任务富有适度的挑战性和吸引力，有助于学生独立思考，体会数学思想和数学思维方式；其次具有“适切性”，其思维含量落点和学生的最近发展区是匹配的，多数学生通过“跳一跳”能够“摘到桃子”。因此，在设计和选择学习素材时，我们需要关注情境性素材的抽象转化与直观表征，促使学生“由表及里地想”；需要关注比照性素材的关系概括与类比推理，促使学生“居高临下地想”；需要关注梳理性素材的方法追溯与策略提炼，促使学生“瞻前顾后地想”。

一、情境性素材，发展数学眼光，促进抽象转化和直观表征

用数学的思维方式想问题，首先得善于运用数学眼光从实际事物中发现蕴含的数学问题。而数学问题的发现、提取过程，是一个“由表及里”的数学化过程，它本身就是数学思考的行为，且需要敏锐的数学眼光。当然，数学眼光的培养需要长期的积累，尤其离不开借助情境性学习素材所进行的抽象转化和直观表征训练。

一方面，数学眼光讲求透过生活现象发现数学问题，能够将具体的现实情境问题抽象转化为数学问题。这就要求在选取和设计具体情境话题时，既要充分考虑素材对于学生的吸引力，又要关注到数学本质，有利于实现初步的数学化。比如，教学“圆的认识”时，特级教师朱乐平呈现了学生熟悉的套圈游戏，讨论“一字形”、“正方形”、“圆形”三种站队方案游戏的公平性，并即时把套圈游戏的实物情景图抽象为“定点”的数学示意图，学生自然从“哪种套圈游戏方案公平”的生活问题的讨论进入“两点之间距离是否相等”这一数学本质问题的思考。而特级教师黄爱华教学“圆的认识”时，呈现的是生活中常见的窨井盖图，抛出了“为什么窨井盖要做成圆形”这一学生既熟悉又陌生的生活问题，学生即刻进入了圆的本质特点的思考与讨论。两位名师学习素材选取不尽相同，但都是情境性素材，且体现了贯通生活问题与数学本质的特点。

另一方面，数学眼光讲求透过错综复杂的数学情境发现内隐的关键问题，能够通过直观表征将其予以外显，逼近本质思考。这就要求我们对于本身比较复杂抽象、关键信息隐含的数学问题，要有意识地引导学生通过画一画、摆一摆等外在的表现形式来寻找思考的线索。比如，在人教版归总问题“妈妈的钱买6元一个的碗，正好可以买6个。用这些钱买9元一个的碗，可以买几个？”中，由于“这些钱”这条关键信息是隐含的，学生在解读题意时往往感知刺激不强烈，一时无法捕捉到总量不变这一本质特点。教学中就需要介入线段图表征题意，要在线段图上反映出总量长度相等，又要用不等长的线段区分出“6元”“9元”价钱不一，学生往往在“等长”和“不等长”的图示表达中顾此失彼。在表征中，学生容易出现类似下图的典型错误：

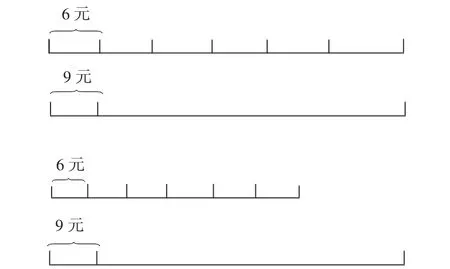
此时围绕“整条线段表示什么？”“同样长是反映哪条信息？”“不同样长想表达什么信息？”等系列问题开展讨论，学生在外化的线段图“说长道短”中梳理了各信息之间的内在联系，较好感知了归总问题的本质特点。

情境性素材的设计和选择，既要善于将学生置身于“它和我们学过的什么数学知识有关联”的思考，实现生活情境数学化；又要善于让学生利用几何直观手段来描述分析数学情境，实现抽象数学问题直观化，促发学生由表及里地想，从而培养和发展学生的数学眼光。

二、比照性素材，追求整体感知，促进关系概括和类比推理

学会思考的本质是学会概括、学会推理，而支持概括能力和推理能力最为核心的要素是关系的感知与联想。教学中，要善于运用整体感知的方式，扩展感知面、拉长感知过程，让学生在“是什么，不是什么”的对比材料和“它们之间有什么联系”的类比材料中实现自我概括与判断推理，充分发挥迁移内化的作用，培养学生的概括能力和推理能力。

比如，在概念教学中许多教师习惯于将概念属性进行分解，给定若干个学习材料组织学生进行分步观察比较、逐级抽取概念属性，最终完成整个概念的归纳概括，学生经历的是从局部到整体的过程感知。而概念各种属性之间关系的发现，更有赖于整体感知，更需借助于整体性对比材料，让学生置身于对概念全部属性的一次性观察、比较、分析和归纳概括。以认识长方形为例，可以呈现下列整组材料让学生进行观察思考。

（1）这些是长方形。

（2）这些不是长方形。

（3）哪些是长方形？

（4）你能用自己的话说一说什么是长方形吗？

（5）根据自己写下的定义，仔细检查是否适合上面举出的例子。

（6）反馈交流，归纳长方形特征。

上述概念的概括过程，教师先直接提供“这些是长方形”的肯定例证和“这些不是长方形”的否定例证，再提供一组具体例证让学生进行判别，然后组织学生尝试概括特征并提醒学生进行比对，最后进行交流概括。在这个对比分析过程中，一直是以图形的整体特征来推进，促使学生从边和角两个核心要素对长方形与其他图形之间关系作出分化与类化，有效提升了概括能力。

在规律、性质序列学习中，后续规律、性质的学习通常是采用类比推理的方式归纳、概括出新结论。教学中，要积极寻找新旧事物间相似性材料，激发学生在原有结论基础上进行推理，试着猜想、概括新结论，并在举例验证中确认新结论，实现有意义的同化。比如，在比的基本性质之前学习了商不变的性质和分数的基本性质，学生已经积累了一些归纳规律（性质）的经验，教学中可以通过“3÷5=（ ）÷10=12÷（ ）”、“”一组材料让学生进行回忆复习，并类比比的基本性质。

概念间关系的感知与联想，“仰仗”于学习素材对于学习者的外在刺激和内化反映。在概念、法则、定律、性质等内容教学中，教师要积极搭建概括、推理交锋的平台，提供一组或几组对比、类比材料，引导学生从整体、宏观的角度居高临下地思考，以切实提升学生分化、分类水平，发展自我概括、自我推理能力。

三、梳理性素材，着力路径习得，促进方法追溯和策略凝练

当学生明确要想的数学问题后，思考的方法就尤为重要了。教学中，要充分让学生经历想问题的过程，并通过学习素材的梳理，体会想问题的思路与方法，积累想问题的经验，形成一些想问题的策略。根据问题解决的步骤，想问题方法与策略的回顾梳理，一般有问题解决前的启蒙式梳理和问题解决后的反思式梳理两种情形。

问题解决前的启蒙式梳理，一方面通过学习素材回忆原先问题解决的基本思路和一般步骤，考量其能否在新问题上加以借鉴，起到定向作用；另一方面，如果原有的思路方法不能在新问题中直接应用，两者间的缺口或困难是什么必须加以明确，以起到聚焦作用。比如在用假设法解决工程问题中，教材安排了“一条道路，如果甲队单独修，12天修完；如果乙队单独修，18天才能修完。如果两队合修，多少天能修完？”的实际问题。前测显示，绝大多数学生由于第一次面临这种新问题，缺乏方法层面的经验，无法自主产生“假设法”这一策略。教学中，可以先通过“24吨救灾物资运送到鲁甸，甲运输公司6天能运完，乙运输公司只要3天，如果两个运输公司一起运，几天能运完？”具体问题的解决和思路步骤分析，再给出上述问题，促发学生联想到“增加具体路长这个条件，新问题就转化为老问题”这一节点，此时就有部分学生自主萌生假设法。又如，圆的面积公式推导中，首先回顾平行四边形、三角形和梯形面积公式推导的过程，得出转化方法和推导的步骤，然后再组织学生在原有的割补法和倍拼法中进行思辨“转化方法中的割补法和倍拼法，你觉得对圆来说哪一种方法更合适？为什么？”这就是一个探究方法定向选择的梳理过程。

问题解决后的反思式梳理，重在归类比较、融会贯通。通过反思“我们刚才解决问题的方法和原来的方法有什么相同和区别？”“如果碰上类似的问题，该如何解决？”等问题，促使学生对一类问题解决的方法进行梳理，从而提升能力。比如，“三位数乘两位数”是在多位数乘一位数、两位数乘两位数基础上学习的，也是整数乘法学习的最后阶段，教学中有必要围绕“影响整数乘法笔算的基本核心要素有哪些”进行计算规则的提炼和归类。可以通过一组反思问题来梳理：问题1“三位数乘两位数与三位数乘一位数在计算方法上有哪些异同？”组织学生明确两者在乘的顺序（数位上）是一致的，不同的是积的层数不同；问题2“三位数乘两位数与两位数乘两位数在计算方法上有哪些异同？”组织学生明确两者都需要两层积叠加，不同的是后者每层积要少乘一个数位；问题3“刚才我们是从哪几个方面对笔算乘法进行比较思考的？”引导学生发现，整数笔算乘法主要从乘的顺序、积的叠加层数两个核心要素对计算法则进行关注。此时，再抛出问题4“如果遇上三位数乘三位数笔算乘法，你认为在计算方法上会有什么特点？”学生已经能够水到渠成地从整数乘法的核心要素进行思考。

事实上，无论是学习方法的追溯还是解决问题策略的提炼，都需要梳理性学习材料加以刺激，只有在“原来怎么想”、“现在怎么想”和“以后怎么想”的不断沟通梳理中，数学思考的意识和能力才能日益增长。

（责编 金 铃）

G623.5

A

1007-9068（2015）14-005