极端环境下导管架平台连续倒塌鲁棒性评估

朱本瑞，陈国明，林 红，刘红兵，胡春友

（1.中国石油大学海洋油气装备与安全技术研究中心，山东青岛266580；2.天津大学建筑工程学院，天津300072）

极端环境下导管架平台连续倒塌鲁棒性评估

朱本瑞1，2，陈国明1，林 红1，刘红兵1，胡春友1

（1.中国石油大学海洋油气装备与安全技术研究中心，山东青岛266580；2.天津大学建筑工程学院，天津300072）

基于Pushover和AP法分析平台结构极限状态及剩余强度储备比，探讨不同类别承载模式的构件对平台结构抗倒塌能力的影响规律；采用WDSR、WRIF和WSRF确定性指标，评估平台结构鲁棒性和构件重要度。考虑平台抗力受环境载荷变化的影响，基于MSA和LSIA建立随机平台在随机载荷下的可靠度评估方法，提出导管架平台“安全评定图”概念，对服役平台全尺度载荷下的安全性进行标定，在此基础上，对导管架平台进行概率鲁棒性评估。研究表明：平台抗力对水平撑构件的失效不敏感，水平撑的确定性鲁棒性指标较大，可视为冗余性构件；斜撑对保证平台结构的鲁棒性起关键作用；这类构件的失效对结构承载能力影响相对显著，在进行平台结构鲁棒性设计时，应保证其具有足够的强度与韧性。提出的“安全评定图”能够提高平台概率鲁棒性评估的计算精度。

导管架平台；极限承载能力；失效概率；连续倒塌；鲁棒性评估

超强台风是导致导管架平台发生连续倒塌破坏的主要极端环境载荷之一。2002—2005年，发生在墨西哥湾的台风Lili、Ivan、Katrina和Rita摧毁112座固定式平台［1-2］，使得海洋平台的抗连续倒塌分析成为研究热点。连续倒塌概念最先在建筑类结构设计理论中提出，鲁棒性评估是防止结构发生连续倒塌的重要做法。目前，鲁棒性已成为衡量建筑结构抗倒塌能力的重要评估指标［3-4］。然而，截止目前为止，最新版的导管架平台设计规范API RP 2A中仍未涉及鲁棒性分析的相关内容［5］，中国《钢结构设计规范》中的“强节点弱构件”和“设置多道防线”等概念蕴含着鲁棒性的思想［6］，但尚未给出明确的规定与推荐做法。吕大刚等［7］给出建筑结构鲁棒性的新定义，并对钢筋混泥土框架结构的抗震鲁棒性进行了定量评价，但现有的鲁棒性评估做法主要局限于建筑结构范畴中，在海洋导管架平台结构的抗台风设计与评估中应用较少。为此，笔者综合考虑钢制固定式海洋平台自身的结构特点及倒塌灾变载荷的不同，将结构鲁棒性评估理论引入到导管架平台的抗倒塌性能评估中，分别从基于确定性和基于概率分析的两类鲁棒性指标对导管架平台结构的鲁棒性展开研究。

1 导管架平台确定性鲁棒性评估

鲁棒性侧重于评价结构整体对局部破坏的抵抗能力，目前，主要通过“改变路径法”（alternate path method，简称AP法）进行［8］。AP法通过假定结构中承重构件发生损伤而失效，在计算过程中将其从结构中移除，然后分析剩余结构是否能够形成新的载荷传递路径，进而判断结构是否发生连续倒塌。

1.1 确定性鲁棒性评估指标

鲁棒性与结构的极限承载能力、延性、冗余度等性能密切相关，表征结构“忍受”初始损伤的能力。可将导管架平台的剩余强度储备比WDSR、剩余影响系数WRIF、强度冗余系数WSRF作为结构鲁棒性评估的指标，即

其中

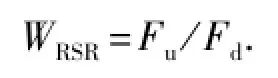
式中，Fsu为损伤平台的极限承载能力；Fd为平台的设计环境载荷；Fu为完好平台的极限承载能力；WRSR为完好平台的强度储备比。

基于确定性评估指标评估平台是否发生连续倒塌的准则为：当WDSR＞1，或WRIF＞1/WRSR，或WSRF＞WRSR/（WRSR-1）时，损伤平台在遭遇设计载荷时不会发生连续倒塌，否则将发生连续倒塌。

确定性鲁棒性评估指标WRIF亦可作为平台构件重要性的测度，即构件移除后，WRIF越小，说明构件越重要；反之，WRIF越接近于1，则构件越不重要。由此，本文中将构件重要度划分为非冗余性构件、关键构件、重要构件、冗余性构件4类，并给出对应的评价准则，见表1。

表1 导管架平台杆件重要度评价准则Table 1 Components important evaluation criterion of jacket platforms

1.2 导管架平台Pushover分析

基于确定性指标的鲁棒性分析关键在于确定平台结构的极限承载能力。平台的极限承载能力可通过Pushover方法进行评估［9］。目前，API、ISO以及DNV规范均普遍推荐使用该方法。Pushover是对结构施加设计环境载荷，考虑材料与几何非线性因素，采用增量方式逐级对设计载荷进行放大，直至结构发生倒塌，其分析原理如图1所示。

图1 导管架Pushover分析原理图Fig.1 Pushover analysis schematic of jacket platforms

由图1可知，Pushover分析能够得到平台结构弹性与弹塑性全阶段的响应信息与参数，从而有效地评估平台结构的整体鲁棒性及局部结构失效后的响应状态。

2 导管架平台概率鲁棒性评估

2.1 概率鲁棒性评估指标

概率冗余度指标（probabilistic redundancy index，PRI）WPRI体现了系统本身和外载荷的不确定性［10］，定义为平台结构损伤前后系统倒塌失效概率的相对变化，即

式中，PS和PW分别为平台损伤状态和完好状态的倒塌失效概率。

显然，该指标取值越小表明系统的鲁棒性越好。

采用可靠性指标描述结构的鲁棒性，相应的可靠度冗余度指标βR为

式中，βS和βW分别为损伤结构和完好结构的可靠性指标。

该鲁棒性指标的取值范围为1～∞，与WPRI相反，βR取值越大表明系统的鲁棒性越强。

2.2 平台失效概率计算的条带分析法

采用概率冗余度指标进行导管架平台鲁棒性评估时须计算平台倒塌的失效概率或可靠度。传统可靠性分析在建立导管架平台极限状态函数时，往往忽略环境载荷对平台抗力的影响［11-12］；然而研究表明，平台极限抗力与结构载荷侧向分布息息相关，特别在超强台风下引起的极端环境载荷下平台抗力随上浪高度的增加而降低［9］，为此，建立平台极限状态函数为

式中，X为随机变量的向量，即｛H，γs，γj，γd｝；H为波高；R为平台系统抗力；Qj、Qw分别为波流载荷效应（作用于导管架上）和风载荷效应；Qd为极端环境引起的甲板上浪载荷效应；γs为平台系统抗力的偏置系数；γj和γd分别为对应于载荷效应Qj和Qd的偏置系数。

式（6）将抗力R视为波高H的函数，从而考虑了环境载荷对平台抗力的影响。然而，上述改变使得分析问题转变为求解随机平台在随机环境载荷下的复杂耦合计算难题，目前，这类问题求解还没有较好的方法。徐长航等［13］提出支持向量机法，采用有界概率分布建立了平台响应与载荷响应关系的统一概率分布函数，但其方法难以解决以极限承载能力为失效函数的非线性不收敛求解与抽样问题。为此，笔者借鉴建筑结构概率抗震设计的思想［14］，提出导管架平台极端环境下的多条带分析（multiple strip analysis，MSA）法，并结合载荷序列增量分析（load sequence incremental analysis，LSIA）［15］，实现平台抗力与载荷效应的解耦，从而建立极端环境载荷下的平台结构倒塌失效概率计算方法，为评估平台结构的鲁棒性提供有利的工具。

考虑海洋环境载荷的特点，影响导管架平台载荷分布最显著的因素为波浪载荷［16］，因此基于MSA思想，将波高离散为一系列工况，由于低于操作工况的波高对平台载荷分布变化的影响很小，故波高下限取一年一遇波高参数H1，上限则采用由LSIA确定的倒塌波高HCP，考虑到甲板上浪载荷对平台载荷分布影响较大，故取［H1，Hwd］和［Hwd，HCP］两个区间（Hwd为甲板上浪发生的临界波高）；然后分别对每种工况进行Pushover分析，记λDP为载荷效应x大于特定需求参数WDP的平均年超越概率，于是有

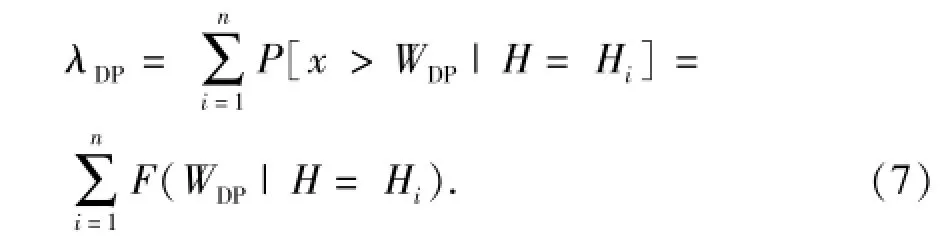
式中，P（x＞WDP|H=Hi）为波高Hi时平台载荷效应大于WDP的条件概率；F（WDP|H=Hi）为波高Hi时WDP的条件累积分布函数。

于是，由全概率公式，平台系统总的失效概率为

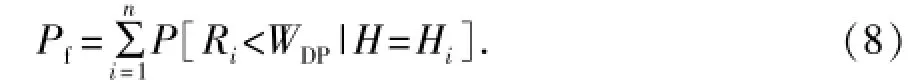
式中，Ri表示波高为Hi时计算得到的平台抗力。

当对于任意波高Hi下平台抗力偏置系数γs以及载荷效应偏置系数γj和γd服从相同分布时，则式（7）和（8）可写成积分的形式，有

式中，P（H=Hi）为波高Hi的发生概率，由波高的概率分布计算。

波浪周期T对环境载荷产生的影响采用DNV规范推荐的经验公式进行考虑［17］，即

式中，a和b为经验参数，根据基于场址的不同重现期下的环境载荷参数进行拟合确定。

3 算例分析

3.1 平台结构有限元模型与环境参数

某海洋平台设计水深107 m，导管架由4腿7层结构组成；平台上部尺寸为40 m×45 m，底层甲板高程为16.5 m，导管架采用4裙12桩安装于海底，建立该平台结构有限元模型，如图2（a）所示。采用AP法移除构件对应的编号如图2（b）所示，其中，斜撑构件采用“X”表示，水平撑构件采用“L”表示。

考虑到鲁棒性分析涉及结构非线性阶段力学行为的研究，建模时应充分考虑模拟单元的力学特性及材料非线性。选用3D弹塑性单元PIPE288和PIPE20分别建立平台导管架与桩腿部分，材料选取双线性随动强化模型；桩-土非线性相互作用采用弹簧单元COMBIN39模拟，弹簧实常数通过平台井位处土层设计强度参数计算得到的p-y曲线、t-z曲线以及桩端q-z曲线定义。

图2 平台有限元模型及构件编号Fig.2 FEM of platform and identifier of components

根据中国科学院南海海洋研究所对1948—2008年间的环境载荷资料，采用三参数Weibull极值分布对环境载荷要素进行推算，由极大似然估计法得到不同环境要素的Weibull分布参数估计值，见表2。

由表2中估计参数，可计算得到该海域不同重现期对应的风速、波高、周期及流速的极值（具体数值参见文献［15］），从而为平台概率鲁棒性评估提供基础数据。

表2 环境载荷Weibull参数估计Table 2 Weibull parameters estimate of environmental loads

3.2 基于确定性指标的鲁棒性评估

对平台施加100年一遇的设计环境载荷（波高H=22.4 m，最大风速44.2 m/s），采用Pushover对不同构件移除后的损伤平台进行极限承载能力分析，得到其抗力曲线如图3所示（根据构件受力状态分析，将斜撑构件分为受压和受拉两类）。

由图3（a）可知，完好平台极限承载能力为84.28 MN，水平撑构件移除后平台极限承载能力几乎不变，WRIF约等于1，说明水平撑对平台结构的抗倒塌性能影响微小，其鲁棒性指标高，这类构件为冗余性构件；由图3（b）和图3（c）可知，移除斜撑构件后，平台刚度略有降低，极限承载能力存在不同程度的衰减。观察图3（b）可知，移除受压斜撑后，除X07工况与完好平台倒塌模式一致外，其余工况失效模式均表现为较好的延性倒塌；由图3（c）可知，移除受拉构件后，除X05工况表现为一定的冗余性外，剩余工况均为脆性倒塌，且平台响应均表现为由线性状态直接演变为倒塌状态，这说明受拉构件对平台冗余性以及抗倒塌能力的影响较大，因此，提高构件材料的极限抗拉强度可改善平台的抗连续倒塌性能。

计算完好平台的WRSR为4.98，故当WDSR＞1，或WRIF＞0.2，或WSRF＞1.25时，损伤平台在百年一遇环境载荷下不会发生连续倒塌，由此，计算得到基于确定性指标的平台鲁棒性评估结果，见表3。

由表3可知，所有拆除工况均满足平台不发生连续倒塌的准则要求，说明该平台具有良好的适用性与鲁棒性；基于鲁棒性指标WRIF的评估结果可合理制定平台服役过程中的水下检测计划以及构件优先顺序，即X07为C4类构件，可不进行检测或减少其检测次数，而X03、X10、X12为C1类构件，应作为重点检测对象，一旦发现构件存在损伤或缺陷，应及时进行维修，以保证平台服役中的安全性。

进一步分析移除构件对平台鲁棒性影响的规律如图4所示（以X斜撑为一个“单元”进行排序）。由图4（a）～（c）可知，X斜撑的4个子构件对平台鲁棒性的影响具有统一规律，呈现“强压弱拉”现象，即鲁棒性指标顺序为XC2＞XC1＞XT2＞XT1，如图4（d）所示。以上规律可进一步阐明为：①受压构件的鲁棒性指标大于受拉构件，记为XC＞XT；②承载模式相同的两个子构件（受拉或受压），下层构件鲁棒性指标大于上层构件，即XC（T）2＞XC（T）1。平台构件重要度与鲁棒性指标成反比，因此构件重要度规律与以上结论相反，即呈现“弱压强拉”规律，该规律可作为平台检测测点选择与布置的依据。

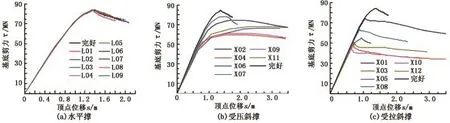
图3 不同构件移除后的平台UBCCFig.3 Platform UBCC after different braces removed

表3 基于确定性指标的平台鲁棒评估结果Table 3 Robustness evaluation results of platform based on deterministic indexes

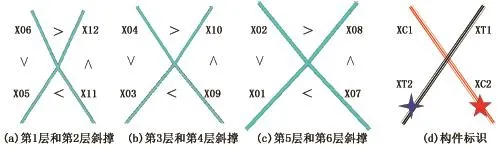
图4 平台构件对结构鲁棒性影响规律Fig.4 Influence of platform components on robustness

3.3 基于概率性指标的鲁棒性评估

采用牛顿法求得Stokes 5th波对应的临界上浪波高Hwd为25.9 m；基于LSIA确定完好平台倒塌重现期为1.3×105a，对应的倒塌波高HCP为31.8 m；由表2求得，操作工况波高H1=7.23 m；由此，根据MSA方法，将波高离散为｛7.23，17.5，22.4，25.9｝和｛26.9，28.1，28.9，29.7，30.95，31.60｝共计10种工况，分别对每种工况进行Pushover分析，将平台的极限承载能力与载荷效应作于同一坐标系中，如图5所示。

由图5可知，当不考虑随机变量对平台抗力与载荷效应的影响时，则R与Q为确定性关系，两者的比值即为平台的安全系数［n］，特别地，当波高H为设计环境载荷时，R/Q即为平台强度储备比WRSR；若考虑随机变量时，平台的安全裕量可采用可靠度或失效概率进行衡量（如H=17.5 m时所示）。由上述分析可知，图5包含了平台在全尺度载荷强度下安全评估的信息和参数，对于掌握平台能力与需求响应性能，进行确定性评估以及不确定性概率计算均具有重要意义，为此，将其称为平台结构的“安全评定图”（safety assessment figure，SAF）。显然，采用SAF对服役平台进行“标定”，可清晰地展示其在服役环境载荷下的响应与安全度。

图5 平台能力与需求参数随波高的变化Fig.5 Variation of capacity and demand parameters of platform with wave height

分析图5中抗力与载荷效应曲线的规律可知，对于文中算例而言，当H＜Hwd时，即甲板上浪载荷发生前，平台的安全裕量较大；当H＞Hwd时，平台抗力开始衰减，而载荷呈指数增加，因此，平台安全裕量随波高的增加而较快降低；在临界上浪高度时的平台抗力最大，且抗力与载荷效应的差值最大，即结构安全裕量最大。

由上述10种计算工况拟合得到平台极限承载能力R（H）与载荷效应Qj（H）和Qd（H）计算公式，取平台的γs、γj和γd服从均值为1，变异系数分别为0.15，0.20和0.30的对数正态分布［18］，由此，求得完好平台失效概率随波高的变化规律，如图6所示。

由图6可知，平台失效概率随波高的变化曲线呈现双峰式分布，在临界甲板上浪波高Hwd时，失效概率出现一个极小值，显然，这是由于平台SAF的安全裕量最大造成的；当波高较大或较小时，平台失效概率均较小，这是因为波高极大（小）值发生的概率较小。由式（10）计算得平台总失效概率Pf= 1.075×10-4，对应的可靠度指标为3.70；而仅考虑百年一遇环境载荷时，平台失效概率为1.467× 10-5，可靠度指标为4.178。可见，相对于传统可靠性评估，基于本文中提出的SAF进行平台可靠性计算时，能够有效地考虑平台环境条件改变对平台失效概率的影响，使得评估结果更加精确。

同理，可求得平台在不同构件移除后的失效概率与可靠度，由于采用MSA时，需要进行大量的非线性计算，这里仅对移除斜撑构件进行分析，由此，得到平台的概率鲁棒性指标评估结果如图7所示。

图6 平台失效概率与波高的变化关系Fig.6 Relationship between the failure probability and wave height

图7 基于概率分析的平台鲁棒性评估结果Fig.7 Probabilistic robustness evaluation results of platform

由图7可知，移除构件X07后，WPRI为最小值0.425（对应的βR为最大值40.71）；移除构件X10时，WPRI最大值为11.81（对应的βR为最小值5.24），即X07对应的鲁棒性最强，构件X10鲁棒性最弱，为平台的弱点位置，在平台设计或检测时，鲁棒性弱者应作为重点考虑对象。对比表3和图7可知，基于概率分析的鲁棒性评估与确定性鲁棒性评估结果一致，这是由于斜撑“移除”后对平台抗力衰减影响较大，而对载荷效应影响较小造成的。

4 结 论

（1）平台抗力对水平撑构件的失效不敏感，水平撑的确定性鲁棒性指标较大，可视为冗余性构件；斜撑对保证平台结构的冗余性起关键作用，这类构件的失效对结构承载能力影响相对显著，在进行平台结构鲁棒性设计时，应保证其具有足够的强度与韧性。

（2）X斜撑的4个子构件对平台鲁棒性的影响具有统一规律，呈现强压弱拉现象，即受压构件鲁棒性指标大于受拉构件；承载模式相同的两个子构件，下层构件鲁棒性指标大于上层构件的。

（3）提出的极端环境下平台失效概率的多条带分析（MSA）法相对仅考虑百年一遇环境载荷进行评估时，可提高平台可靠性分析的精度；结合LSIA方法，提出的导管架平台“安全评定图”可清晰地展示平台在服役环境载荷下的响应与安全度。

（4）基于概率分析的鲁棒性评估能够综合考虑平台冗余性、极限承载能力、随机变量及可靠度的影响，相对确定性鲁棒性评估指标具有不可替代的优势。

［1］ PUSKAR F J，SPONG R E，KU A，et al.Assessment of fixed offshore platform performance in Hurricane Ivan［R］.OTC 18325，2006.

［2］ PUSKAR F J，VERRET S.Assessment of fixed offshore platform performance in Hurricanes Katrina and Rita［R］.MMS Project-578，2007.

［3］ 胡晓斌，钱稼茹.结构连续倒塌分析与设计方法综述［J］.建筑结构，2006，36（s1）：79-83. HU Xiaobin，QIAN Jiaru.Overview of analysis and design approaches for progressive collapse of structures［J］. Building Structure，2006，36（s1）：79-83.

［4］ BAKER J W，SCHUBERT M，FABER M H.On the assessment of robustness［J］.Structural Safety，2008，30（3）：253-267.

［5］ American Petroleum Institute.API RP 2A-WSD 2007 Recommended practice for planning，design and constructing fixed offshore platforms-working stress design［S］.Washington D C：API Publishing Services，2007.

［6］ 张启文，夏志斌，黄友明，等.GB50017-2003钢结构设计规范［S］.北京：中国计划出版社，2003.

［7］ 吕大刚，宋鹏彦，崔双双，等.结构鲁棒性及其评价指标［J］.建筑结构学报，2011，32（11）：44-54. LÜ Dagang，SONG Pengyan，CUI Shuangshuang，et al. Structural robustness and its assessment indicators［J］. Journal of Building Structures，2001，32（11）：44-54.

［8］ 胡晓斌，钱稼茹.结构连续倒塌分析改变路径法研究［J］.四川建筑科学研究，2008，34（4）：8-13. HU Xiaobin，QIAN Jiaru.Study on alternate path method of structural progressive collapse analysis［J］.Sichuan Building Science，2008，34（4）：8-13.

［9］ 朱本瑞，陈国明，刘康，等.深水导管架平台抗台风极限承载能力［J］.石油学报，2014，35（1）：152-158. ZHU Benrui，CHEN Guoming，LIU Kang，et al.Typhoon-resistant ultimate bearing capacity of deep-water jacket platforms［J］.Acta Petrolei Sinica，2014，35（1）：152-158.

［10］ 林红，陈国明，朱本瑞，等.海洋石油平台结构全寿命周期动态鲁棒性分析［J］.石油学报，2015，36（2）：246-252. LIN Hong，CHEN Guoming，ZHU Benrui，et al.Dynamic robustness analysis of the offshore platform in the whole life cycle［J］.Acta Petrolei Sinica，2015，36（2）：246-252.

［11］ HEREDIA-ZAVONI E，CAMPOS D，RAMIÍREZ G. Reliability based assessment of deck elevations for offshore jacket platforms［J］.Journal of Offshore Mechanics and Arctic Engineering，2004，126（4）：331-336.

［12］ 陈团海，陈国明，许亮斌.基于台风验证载荷的平台时变可靠性分析与更新［J］.中国石油大学学报（自然科学版），2011，35（3）：129-134. CHEN Tuanhai，CHEN Guoming，XU Liangbin.Timedependent reliability analysis and updating of offshore platforms based on typhoon proof load［J］.Journal of China University of Petroleum（Edition of Natural Science），2011，35（3）：129-134.

［13］ 徐长航，陈国明，谢静.基于支持向量机和蒙特卡洛的结构可靠性分析方法及应用［J］.中国石油大学学报（自然科学版），2008，32（4）：103-108. XU Changhang，CHEN Guoming，XIE Jing.Structural reliability analysis method based on support vector machines and Monte Carlo and its application［J］.Journal of China University of Petroleum（Edition of Natural Science），2008，32（4）：103-108.

［14］ JALAYER F，CORNELL C A.Alternative non-linear demand estimation methods for probability-based seismic assessments［J］.Earthquake Engineering&Structural Dynamics，2009，38（8）：951-972.

［15］ 朱本瑞，陈国明，林红，等.极端波浪载荷下导管架平台抗倒塌性能评估［J］.中国石油大学学报（自然科学版），2014，38（3）：135-141. ZHU Benrui，CHEN Guoming，LIN Hong，et al.Anticollapse performance assessment of jacket offshore platforms in extreme storm waves［J］.Journal of China University of Petroleum（Edition of Natural Science），2014，38（3）：135-141.

［16］ GOLAFSHANI A A，BAGHERI V，EBRAHIMIAN H，et al.Incremental wave analysis and its application to performance-based assessment of jacket platforms［J］. Journal of Constructional Steel Research，2011，67（10）：1649-1657.

［17］ DNV-RPC 205.Environmental conditions and environmental loads［S］.Norway：Det Norske Veritas，2007.

［18］ MARK M，ETTERDAL B，GRIGORIAN H.Structural reliability assessment of Ekofisk jackets under extreme loading［R］.OTC 13190，2001.

（编辑 沈玉英）

Robustness assessment of jacket platforms for progressive collapse under extreme environmental loading

ZHU Benrui1，2，CHEN Guoming1，LIN Hong1，LIU Hongbing1，HU Chunyou1
（1.Centre for Offshore Engineering and Safety Technology，China University of Petroleum，Qingdao 266580，China；2.School of Civil Engineering，Tianjin University，Tianjin 300072，China）

The ultimate limit state and residual strength reserve ratio of jacket platforms were analyzed based on alternate path（AP）and Pushover methods，and the influence of component types on platforms'anti-collapse capacity was investigated.The certainty indexes of WDSR，WRIFand WSRFwere used to assess the robustness of jacket platforms as well as the importance of components.Considering the impact of environmental loading on the ultimate bearing capacity of jacket platforms，random platform reliability assessment method under random loading was established based on multi strips analysis（MSA）and load sequence incremental analysis（LSIA）.Combining MSA and LSIA，a novel safety assessment figure（SAF）was proposed to evaluate the safety of jacket platforms under full scale environmental loading.Further，probabilistic robustness of the platform was assessed utilizing probabilistic redundancy index.The results show that the resistance of the platform is not sensitive to the failure of horizontal bracings，which can be regarded as the redundant components because their deterministic robustness index is more significant.Diagonal bracings play an important role in ensuring the robustness of platform structures.The failure of this kind of components will affect the capacity of the platform.Therefore，it should be ensured that the strength and toughness are sufficient in the design of jacket platforms.The SAF introduced in this paper can improve the calculation precision of proba-bilistic robustness evaluation.

jacket platforms；ultimate bearing capacity；failure probability；progressive collapse；robustness assessment

TE 951

A

朱本瑞，陈国明，林红，等.极端环境下导管架平台连续倒塌鲁棒性评估［J］.中国石油大学学报（自然科学版），2015，39（6）：138-144.

ZHU Benrui，CHEN Guoming，LIN Hong，et al.Robustness assessment of jacket platforms for progressive collapse under extreme environmental loading［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（6）：138-144.

1673-5005（2015）06-0138-07

10.3969/j.issn.1673-5005.2015.06.019

2015-03-10

国家自然科学基金项目（51079159，51209218，51509184）；中央高校基本科研业务费专项（13CX06079A，15CX05003A）

朱本瑞（1986-），男，讲师，博士，研究方向为海洋石油装备强度与可靠性等。E-mail：zhubenrui@163.com。

陈国明（1962-），男，教授，博士生导师，研究方向为海洋油气工程及装备、油气安全工程等。E-mail：offshore@126.com。