任意偶数阶精度交错网格声波方程数值模拟

2015-11-21吴从辉李红星

东华理工大学学报(自然科学版) 2015年1期

吴从辉，李红星，张智

(1.东华理工大学核工程与地球物理学院，江西南昌 330013;2.桂林理工大学地球科学学院，广西桂林 541004)

地震波场数值模拟是地震学和地震勘探的重要基础，在地震学和地震勘探各个工作环节中都起到重要作用(裴正林等，2004)。通过正演模拟技术，可以模拟地震波在各种地质结构中的传播规律，可为地震资料处理解释中各种方法的应用提供标准的先验数据体，检测方法的实用性(赵海波等，2011;张华等，2012)。

有限差分方法因其计算效率高、占用计算内存小等特点，成为当前最常用的数值模拟方法(张英杰等，2007;吕玉增等，2011)。交错网格技术相对于规则网格在复杂模型模拟和模拟精度等方面都有较大的优势(李红星等，2008;李国平等2010)，交错网格引入的频散明显低于规则网格，因此地震波场数值模拟中交错网格有限差分法得到广泛应用。

为得到高精度的正演模拟结果，本文基于一阶应力-速度声波方程组，运用任意偶数阶精度的交错网格有限差分格式进行了各向同性介质模型中的正演模拟。

1 波动方程的有限差分格式建立

1.1 一阶应力-速度声波方程组

根据弹性力学的分析，可得到动力学方程组和应变应力方程组。二维情况下一阶应力-速度声波方程组(张伯军，2010)如下:

式中K = ρv2，K 为地质体压强，ρ 表示地质体密度，vx表示在x 方向上的速度分量，vz表示在z 方向上的速度分量。

1.2 一阶应力-速度声波方程组交错网格计算实现

一阶应力-速度声波方程组各个物性参量在交错网格中的位置设置如下:

空间网格中，参数P 放置在规则的i，j 节点上。而参数vx在x 方向上位于j +1/2 的半节点上，在z方向上位于规则的i 节点上;参量vz在x 方向上位于规则的j 节点上，在z 方向上位于i+1/2 半节点上(图1)。

时间网格中，参数P 在规则的k 节点上，vx与vz均设置在k +1/2 的半节点上(图2)。

图1 空间维度上的网格点分布Fig.1 The grid point distribution in space domain

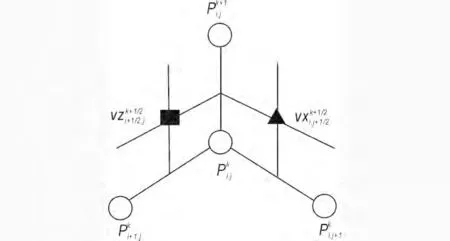
图2 时间维度上的网格点分布Fig.2 The grid point distribution in time domain

1.3 任意偶数阶交错网格差分计算格式实现

本文从Taylor 级数展开式出发，实现了任意偶数阶精度交错网格下的差分格式算法(刘洋等，1998;陈可洋，2009)。设函数U(x)为存在2L +1 阶导数的函数，其在空间i+1/2 半节点处，分别对i 与i +1 点进行泰勒展开处理，得到Ui+1和Ui在i+1/2处的泰勒展开式，即可以得到式(2)和式(3)。

将式(2)与式(3)相减得:

类似上述推导过程，可得任意Ui+m- Ui-m+1(m= 1，2，3…L)的推导结果:

其中m = 1，2，3，…L。由上式可得式(6)，用于计算

解方程式得:

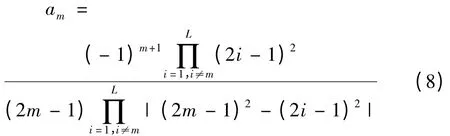
式中am便是任意偶数阶精度交错网格下的一阶导数差分系数，于是:

1.4 一阶应力-速度声波方程组任意偶数阶精交错网格差分算法实现

由式(1)给出的二维情况下一阶应力- 速度方程组，可知需对vx，vz，P 三个参量进行计算。采用时间二阶精度的差分方式对三个参量的时间导数进行计算:

由式(1)结合式(9)及式(10)给出的一阶导数差分计算公式，便可实现时间二阶空间任意偶数阶精度交错网格下的声波方程差分格式(11)。

2 数值模拟中的几个重要问题

2.1 震源函数

震源函数有多种取法，如高斯子波、雷克子波等。在波场数值模拟中，震源函数的选取对模拟结果有重要的影响(张海燕等，2007;董良国等，2004)。本文采用雷克子波作为震源函数。

2.2 稳定性条件

对文中一阶应力-速度声波方程组任意偶数阶精度交错网格有限差分方程，通过平面谐泼的分析(裴正林等，2003)，得出其数值解的稳定性条件:

其中，Δt 为时间域网格步长，Δx、Δz 表示空间域网格步长，vp表示介质的纵波速度，am为相应的交错网格差分算子系数。由式(12)得出交错网格高阶有限差分的稳定性随着差分精度的提高而不断增高(Cao et al.，1997)。

2.3 衰减边界条件

基于在模拟区外围附加吸收层的思想，Cerjan等(1985)提出了衰减边界条件。在模拟区域内，波按照正常的波动传播;当波到达外围衰减区时，波场乘以一个衰减因子G，使其按指数级逐渐衰减。其中:式中N 为衰减区总网格数，i 为衰减区的网格编号(1 ≤i ≤N)，a 为衰减系数。图3 为衰减边界示意图。

图3 衰减边界示意图Fig.3 Pictorial view of the damping boundary condition

李信富等(2007)研究表明，衰减因子参数的选择应采取折中方法，即在取某一较小衰减系数的前提下，设置较少的衰减带网格数使边界的能量反射最小。经对模拟速度和精度的综合考虑，本文a 值选用0.15，N 值为50。那么在衰减区波场计算公式为:

3 精度选取测试及边界效果对比

3.1 差分精度选取测试

理论上说，差分算子的阶数越高，波场模拟结果也越精确。但阶数过高，会造成一定的计算困难(左莹，2007)。那么在效果与效率平衡的基础上，选取合适的差分精度是很有必要的。

为确定合适的差分精度，本文进行了差分精度选取测试。测试模型为均匀各向同性介质模型，模型介质参数:v =1 000 m/s，ρ =1 g/m3。模型大小为1 000 ×1 000 m，x 和z 方向上均有201个网格点，空间网格步长dx，dz 为5 m，dt 为0.4 ms。震源设置在模型中心点处，震源函数频率为25 Hz。采用时间二阶精度，空间不同偶数阶精度进行模拟试算。得到空间不同偶数阶精度下的波场模拟快照(图4)。

通过对比分析，易得出随着空间差分阶数的提高，模拟精度也逐渐增高。空间二阶精度时，存在严重的频散现象;空间四阶精度时，频散现象明显减弱。空间八阶精度时，几乎无频散现象出现;阶数再增加，模拟精度变化不明显。

因此，为得到高精确的正演模拟结果，空间差分精度不得低于八阶。本文的波场模拟都是采用空间八阶精度进行的。

图4 空间不同偶数阶精度下的波场模拟快照Fig.4 Wave field snapshots at diffierent even-order accurate in space

3.2 衰减边界效果对比

测试模型为均匀各向同性介质模型。震源放置在模型中心点处，震源函数频率为25 Hz。选取640 ms 时未使用衰减边界条件和使用衰减边界条件的波场快照进行边界效果对比(图5)。

对比可知，未使用衰减边界条件的波场快照(图5a)，边界反射明显;使用衰减边界条件的模型波场快照(图5b)，未出现边界反射现象。结果表明，衰减边界条件可以有效消除边界反射。

图5 未使用衰减边界和使用衰减边界时波前快照对比图Fig.5 Wave field snapshots without using the attenuation boundary condition and wave field snapshots with using it

4 模型正演模拟

分别对不同类型的模型进行了正演模拟。模拟过程均采用时间二阶空间八阶差分精度。

4.1 水平层状介质模型正演模拟

如图6a 所示水平层状介质模型，模型大小为1 000 ×1 000 m，水平分界面在埋深500 m 处。上层介质参数:v1=1 000 m/s，ρ1=1 g/m3;下层介质参数:v2=1 500 m/s，ρ2=1 g/m。模型剖分为201 ×201个离散节点，空间网格步长为5 m，时间网格步长为0.4 ms。

震源位于水平方向500 m，埋深10 m 处，震源函数频率为25 Hz。对模型进行正演模拟，得到不同时刻的波场快照。

图6b 和图6c 分别为水平层状介质模型560 ms 和600 ms 时刻的波场快照。波场快照中，界面反射波和透射波清晰可见，边界反射被有效吸收，未出现频散现象。图6d 为水平层状介质模型的共炮点记录，直达波及水平分界面z =500 m 处的反射波同相轴清晰。

4.2 倾斜介质模型正演模拟

介质模型依旧采用201 ×201 的网格剖分，空间网格步长为5 m，时间网格步长0.4 ms，第一层介质模型参数:v1=1 000 m/s，ρ1=1 g/m3;第二层介质模型的参数为:v2=1 500 m/s，ρ2=1 g/m3;第三层的介质模型参数为:v3=2 000 m/s，ρ3=1 g/m3。

图6 水平层状介质模型、模型波场快照和共炮点记录Fig.6 The model of horizontal stratified medium、Wave field snapshots and Synthetic seismogram of horizontal stratified medium

图7 倾斜介质模型、模型波场快照和共炮点记录Fig.7 The model of layered medium with tilted interface，Wave field snapshots and Synthetic seismogram of layered medium with tilted interface

倾斜介质模型中倾斜分界面从左边界埋深300 m 处延伸到右边界埋深550 m 处(图7a);水平分界面在埋深z =550 m 处。震源位于水平方向600 m，埋深10 m 处，震源函数频率为25 Hz。同样采用空间八阶时间二阶差分精度进行波场模拟。

图7b 和图7c 分别为倾斜介质模型420 ms 和600 ms 时刻的波场快照，可清晰反映出波在模型中的传播规律。边界反射被有效吸收，但存在轻微频散现象。图7d 为倾斜介质模型的共炮点记录，图中直达波同相轴和界面反射波同相轴清晰明显。边界反射被有效吸收，整体效果良好。

4.3 断层介质模型正演模拟

如图8a 所示断层介质模型，断层分界面中，垂直段在x=600 m 处，从埋深380 m 延伸到520 m。断层水平段一部分在埋深380 m 处，水平坐标x=0至x=600 之间;水平段另一部分在埋深520 m 处，水平坐标x=600 至x =1 000 m 之间。第二、三层介质的水平分界面在z =600 m 处。第一层模型的介质参数为:v1=1 000 m/s，ρ1=1 g/m3;第二层的模型介质参数为:v2=1 500 m/s，ρ2=1 g/m3;第三层的模型介质参数为:v3=2 000 m/s，ρ3=1 g/m3。

震源位于水平方向500 m，埋深10 m 处，震源函数频率为25 Hz。采用同样的差分精度对断层介质模型进行模拟试算。

图8b 和图8c 分别为420 ms 和600 ms 时刻的模型波场快照，充分反映出断层介质模型中波的传播规律。图中可清晰分辨出界面反射波和透射波，以及断层的断点上产生的绕射波;边界反射吸收效果良好，未出现频散现象。图8d 为断层介质模型的共炮点记录。图中直达波、断层界面的反射波及水平界面反射波同相轴清晰。断层上下水平段界面对应的反射波同相轴末端，都伴随着明显的绕射波同相轴，与实际情况相符合。

图8 断层介质模型、模型波场快照和共炮点记录Fig.8 The fault modeling，Wave field snapshots and Synthetic seismogram in the fault modeling

5 结论

高偶数阶交错网格有限差分数值模拟方法可以清晰模拟出波在地下介质中的传播规律。本文方法模拟精度高，计算效率快，能有效压制频散噪音，边界反射吸收效果良好，充分证实了该数值模拟方法的准确性和可行性，具有较高的应用价值。可以推广应用于三维声波高精度正演模拟中，帮助我们深入学习和研究地震波的传播规律，也为地震勘探工作提供了实用的参考价值。

陈可洋.2009.标量声波波动方程高阶交错网格有限差分法［J］. 中国海上石油，21(4):232-236.

董良国，李培明.2004.地震波传播数值模拟中的频散问题［J］.天然气工业，24(6):53-56.

李国平，程利敏.2010.非均匀介质交错网格高阶差分地震波数值模拟［J］.石油天然气学报，32(4):220-225.

李红星，刘财，吴志成，等.2008. 基于BISQ 机制的双相孔隙介质三维数值模拟研究［J］.石油天然气学报，30(2):77-80.

李信富，李小凡，张美根.2007. 伪谱法弹性波场数值模拟中的边界条件［J］.地球物理学进展，22(5):1375-1379.

刘洋，李承楚，牟永光.1998.任意偶数阶精度数值模拟算法［J］. 石油地球物理勘探，33(1):1-10.

吕玉增，熊彬，薛霆虓.2011. 地球物理数据处理基础［M］. 北京:地质出版社:90-106.

裴正林，牟永光.2003.非均匀介质地震波传播交错网格高阶有限差分法模拟［J］.石油大学学报，27(6):17-21.

裴正林，牟永光.2004.地震波传播数值模拟［J］. 地球物理学进展，19(4):933-941.

张伯军.2010.弹性动力学简明教程［M］.北京:科学出版社:35-64.

张海燕，李庆忠.2007.几种常用解析子波的特征分析［J］.石油地球物理勘探，42(6):651-657.

张华，龚育龄.2012.花岗岩裂隙储层各向异性高阶有限差分数值模拟［J］.东华理工大学学报:自然科学版，35(4):416-421.