THE INTEGRAL TYPE GAUGE TRANSFORMATION AND THE ADDITIONAL SYMMETRY FOR THE CONSTRAINED KP HIERARCHY∗
2015-11-21JipengCHENG程纪鹏
Jipeng CHENG(程纪鹏)
Department of Mathematics,China University of Mining and Technology,Xuzhou 221116,China
Jingsong HE(贺劲松)†
Department of Mathematics,Ningbo University,Ningbo 315211,China
THE INTEGRAL TYPE GAUGE TRANSFORMATION AND THE ADDITIONAL SYMMETRY FOR THE CONSTRAINED KP HIERARCHY∗
Jipeng CHENG(程纪鹏)
Department of Mathematics,China University of Mining and Technology,Xuzhou 221116,China
E-mail:chengjp@cumt.edu.cn;chengjp@mail.ustc.edu.cn
Jingsong HE(贺劲松)†
Department of Mathematics,Ningbo University,Ningbo 315211,China
E-mail:hejingsong@nbu.edu.cn
In this paper,the compatibility between the integral type gauge transformation and the additional symmetry of the constrained KP hierarchy is given.And the stringequation constraint in matrix models is also derived.
constrained KP hierarchy;integral type gauge transformation;additional symmetry.
2010 MR Subject Classification 35Q53;37K10;37K40
1 Introduction
The Kadomtsev-Petviashvili(KP)hierarchy(see[1,2]references therein)is one of the most famous integrable systems,which has many important applications in theoretical physics and mathematics,such as 2d quantum gravity[3-5]and infinite-dimensional Lie algebras[6,7]. The constrained KP(cKP)hierarchy[8-11],developed from the point of view of symmetry constraint,can be viewed as an important reduction of the KP hierarchy,which includes many well-known integrable systems,such as the AKNS hierarchy,the Yajima-Oikawa hierarchy and many others[8-10].
The gauge transformation[12,13]is an efficient method to solve the KP hierarchy,which in fact reflects the intrinsic integrability of the KP hierarchy.Chau et al.[12]introduced two types of elementary gauge transformation operators:the differential type TDand the integral type TI.By now,the gauge transformations of many integrable hierarchies related to KP hierarchy were derived,for example,the cKP hierarchy[13-17],the constrained BKP and CKP hierarchy[18,19](cBKP and cCKP),the discrete KP hierarchy[20,21],the q-KP hierarchy[22,23]and so on.The additional symmetry[23-33]is a kind of symmetry depending explicitly onthe space and time variables,involved in so-called string equation and the generalized Virasoro constraints in matrix models of the 2d quantum gravity(see[2,34]and references therein). The corresponding additional symmetry for the cKP hierarchy was constructed in[35-37]by an appropriate modification of the standard additional symmetry flows by adding a set of“ghost”symmetry flows.So it is an interesting problem to show the compatibility between the gauge transformation and the additional symmetry of the cKP hierarchy,in order to show a new inner consistency of the integrable hierarchy.
Here we mainly restrict to the study of the integral type gauge transformation TI.In the construction of the gauge transformation for the BKP and CKP hierarchies[18,19],because of the reduction conditions of the BKP and CKP hierarchies,one can not do the gauge transformation by only using the differential type TD,and instead has to use be the combination of TDand TI.Thus the integral type gauge transformation TIis also very important.In this paper,it is showed that the additional symmetry flows for the cKP hierarchy commute with the integral type gauge transformations preserving the form of cKP,up to shifting of the corresponding additional flows by ordinary time flows,which reflects one of the intrinsic consistences for the cKP hierarchy:the compatibility between the integral type gauge transformations and the additional symmetries.Further,upon the basis of this result,the string-equation constraint in matrix models is also derived.
This paper is organized in the following way.In Section 2,we recall some background on the KP hierarchy.Then the integral type gauge transformation and the additional symmetry for the cKP hierarchy are reviewed in Section 3 and Section 4,respectively.In Section 5,we study the compatibility of the integral type gauge transformation and the additional symmetry for the cKP hierarchy.At last,some conclusions and discussions are given in Section 6.
2 Background on the KP Hierarchy
archy(see[1,2]
therein)is defined as the following Lax equation:

with the Lax operator given by
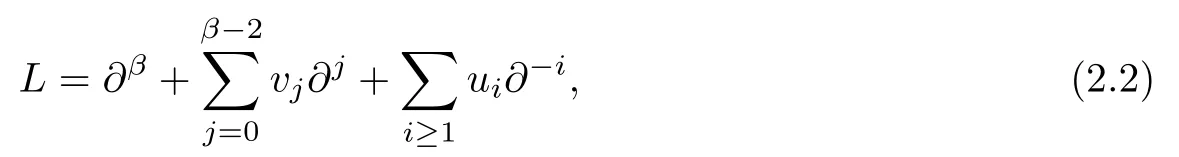
One can also represent the Lax operator in terms of a dressing operator W:

and then the Lax equation(2.1)is equivalent to the Sato's equation:

Define next the Baker-Akhiezer(BA)function by:
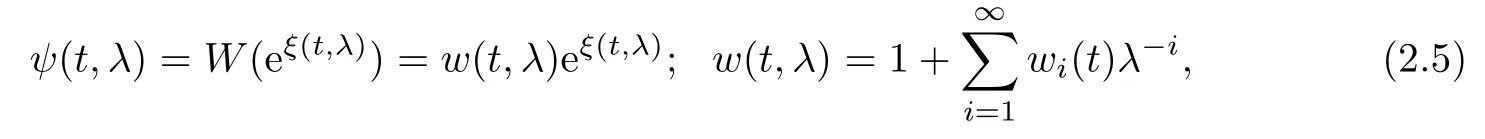
where

Accordingly,there is also an adjoint BA function:

Then the Lax equation(2.1)can be regarded as the compatibility conditions for the following system:

here for any(pseudo-)differential operator A and a function f,the symbol A(f)will indicate the action of A on f,whereas the symbol Af will denote just operator product of A and f,and∗stands for the conjugate operation:(AB)∗=B∗A∗,∂∗=-∂,f∗=f.
The whole KP hierarchy can be characterized by a single function τ(t)called τ-function such that

If the functions q(t)and r(t)satisfy

then we call them the eigenfunction and the adjoint eigenfunction respectively.
The cKP hierarchy[10]is defined by restricting the Lax operator of the ordinary KP hierarchy(2.1)in the following form:

where qiand riare the eigenfunction and adjoint eigenfunction respectively.
3 The Integral Type Gauge Transformation of the cKP Hierarchy
Let L(0)be the Lax operator of the KP hierarchy(2.1),and T be a pseduo-differential operator.If the transformation

such that

still holds for transformed Lax operator L(1),then T is called the gauge transformation operator of the KP hierarchy.
Chau et al.[12]proved there are the following two kinds of the gauge transformation operators:

where χ andµare the eigenfunction and adjoint eigenfunction respectively.The type I transformation is called the differential type,while the type II is called the integral type.In this paper,we mainly study the second one,that is,the integral type.
The gauge transformation of the cKP hierarchy is investigated in[13-15,17].Here we only review some results about the integral type.Assume
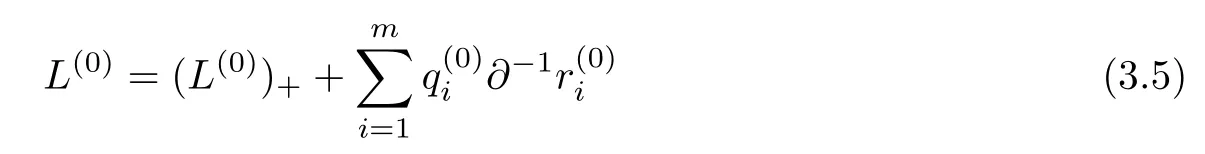
be the Lax operator of the cKP hierarchy.Under the integral type gauge transformation TI(µ),the transformed Lax operator will be:

In order to preserve form(3.5)of the Lax operatoris required to coincide with one of the original adjoint eigenfunctions ofsincein this case.Applying successive the integral type gauge transformations
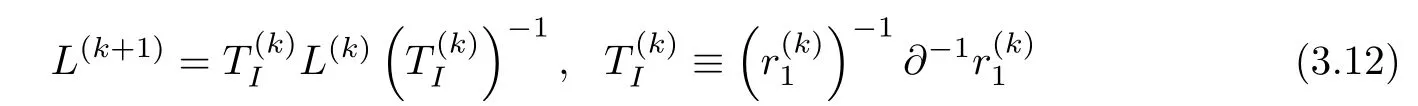
yields:

Successive applications of the integral type gauge transformation will lead to,

Some useful identities involving the integral type gauge transformation of the f∂-1g-form are listed in the lemma below.
Lemma 3.1
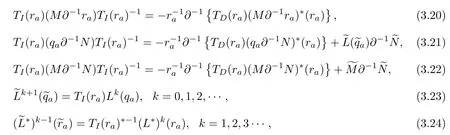
where rais one of the adjoint eigenfunctions of the cKP hierarchy(2.12),M and N are two functions of t,and

Proof First,according to f∂-1-∂-1f=∂-1fx∂-1and∂f-f∂=fx,

Then for(3.23),
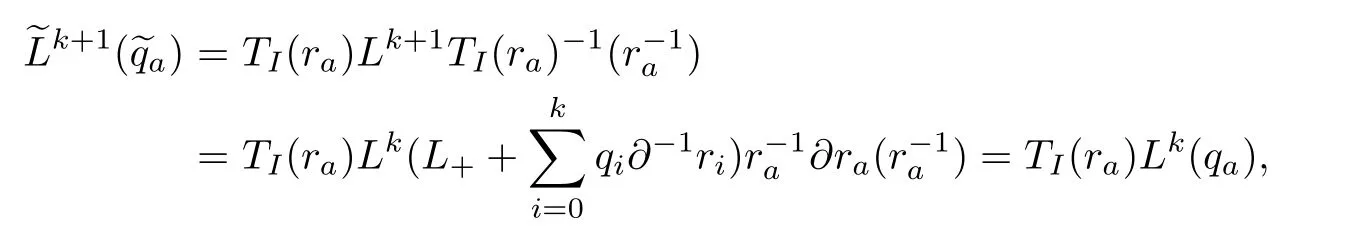
At last,

4 Additional Symmetries of the cKP Hierarchy
The additional symmetry flows[35]for the cKP hierarchy(2.12),spanning the Virasoro algebra,are given by

where M is the Orlov-Schulman operator[25]defined in the dressing the“bare”M(0)operator:

that is,

with(2.4)used in(4.4).Define

which is the essential to ensure the compatibility of the additional Virasoro symmetry with the constraints(2.12)defining the cKP hierarchy
Then accordingly,the actions of the additional symmetry flows on the dressing operators and BA functions are showed that:

The corresponding actions on the eigenfunctions qiand the adjoint eigenfunctions riare derived by considering(∂∗kL)-listed as follows:

5 Additional Symmetries Versus the Integral Type Gauge Transformations for the cKP Hierarchy
In this section,we will restrict to the cKP hierarchy((2.12)for m=1).And thus its Lax operator is given by

In order to investigate the changes of the additional symmetries under the integral type gauge transformation TI(r),some useful lemmas are needed.
Lemma 5.1

Proof According to Lemma 3.1,and(4.5)for m=1,

Lemma 5.2
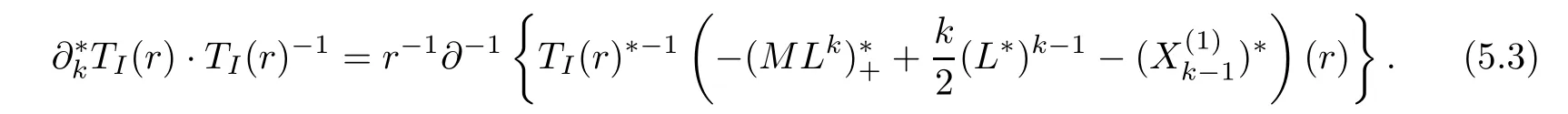
Proof By(4.8),

Proposition 5.3 The additional symmetry flows(4.1)for the cKP hierarchy((2.12)for m=1)commute with the integral type transformations preserving the form of cKP,up toshifting of(4.1)by ordinary time flows,that is,

Proof First,by(4.1),

Then with the help of(5.2),(5.3),and the following useful formula[38]
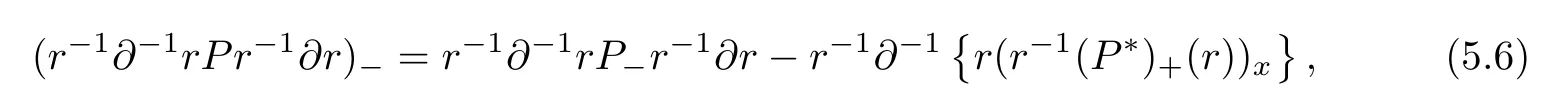
we have

where the following relation[39]is used

At last,the substituting(5.7)into(5.5)gives rise to(5.4). □
Remark when m>1,(5.4)will not hold.In fact,when m>1,(5.2)will become into



Thus from the proof of(5.4),the term of)can not be derived.
The string-equation constraint can be derived through the lowest additional symmetrythat is,
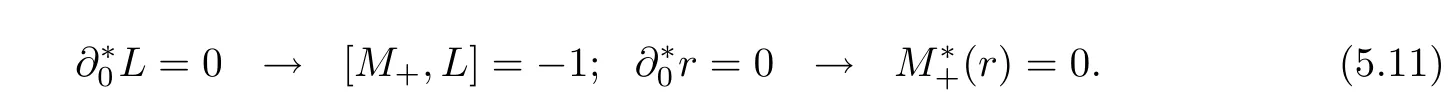
With the help of(2.11),(4.3)and(4.8),the constraints on the Lax operator L and the adjoint eigenfunction r(t)will be derived respectively,

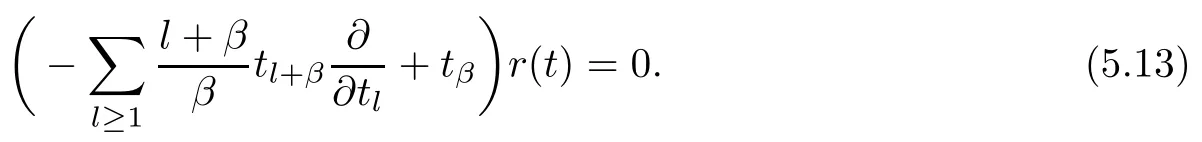
As for the string-equation constraint on the tau functions are showed in the following proposition:
Proposition 5.4 The Wronskian tau functions(3.19)of the cKP hierarchy(5.1)generated by the integral type gauge transformation,invariant under the lowest additional symmetry flow(4.1),satisfy the constraint equation:

Proof First,note that r(k)satisfy the same constraint(5.13)according to Proposition 5.3.Thus from(3.19),we know that

6 Conclusions and Discussions
The interplay of the integral type gauge transformation TIwith the additional symmetry at the instance of the cKP integrable hierarchy is showed in Proposition 5.3(see(5.4)),which shows the intrinsic coordination of the cKP hierarchy,just like the compatibility[35]between the differential type gauge transformation and the additional symmetry.The string-equation constraints,through the lowest additional symmetry∂∗0,on the Lax operator L,the adjoint eigenfunction r(t)and the tau functions,are listed in(5.12)(5.13)and(5.14)respectively.These results show that KP integrable hierarchy is a kind of integrable system with many intrinsic coordinations.
Although this kind of compatibility between the differential type gauge transformation TDand the additional symmetry has been given in[35].But this is not enough to study the cBKP and cCKP because the combination of TDand TIis necessary to satisfy the reduction conditions of the BKP and CKP hierarchies[19].So our results provide a possible basis to explore the consistency of the gauge transformation and the additional symmetry in the cBKP and cCKP hierarchies.This work will be done in a near future.
References
[1]Date E,Jimbo M,Kashiwara M,Miwa T.Transformation groups for soliton equations//Jimbo M,Miwa T. Nonlinear Integrable Systems-Classical Theory and Quantum Theory.Singapore:World Scientific,1983: 39-119
[2]Dickey L A.Soliton Equations and Hamiltonian Systems.2nd ed.Singapore:World Scientific,2003
[3]Witten E.Two dimensional gravity and intersection theory on moduli space.Surveys Diff Geom,1991,1: 243-310
[4]Kontsevich M.Intersection theory on the moduli space of curves and the matrix Airy function.Comm Math Phys,1992,147:1-23
[5]Adler M,van Moerbeke P.A matrix integral solutionto two-dimensional Wpgravity.Comm Math Phys,1992,147:25-56
[6]Kac V.Infinite Dimensional Lie Algebras.3rd ed.Cambridge Univ Press,1990
[7]Jimbo M,Miwa T.Solitons and infinite dimensional Lie algebras.Publ RIMS,Kyoto Univ,1983,19: 943-1001
[8]Cheng Y,Li Y S.The constraint of the KP equation and its special solutions.Phys Lett A,1991,157: 22-26
[9]Konopelchenko B,Sidorenko J,Strampp W.(1+1)-dimensional integrable systems as symmetry constraints of(2+1)-dimensional systems.Phys Lett A,1991,157:17-21
[10]Cheng Y.Constraints of the KP hierarchy.J Math Phys,1992,33:3774-3782
[11]Li C Z,Tian K L,He J S,Cheng Y.The recursion operator for a constrained CKP hierarchy.Acta Math Sci,2011,31B(4):1295-1302
[12]Chau L L,Shaw J C,Yen H C.Solving the KP hierarchy by gauge transformations.Comm Math Phys,1992,149:263-278
[13]Oevel W.Darboux theorems and Wronskian formulas for integrable system I:constrained KP flows.Physica A,1993,195:533-576
[14]Aratyn H,Nissimov E,Pacheva S.Darboux-Backlund solutions of SL(p,q)KP-KdV hierarchies,constrained generalized Toda lattices,and two-matrix string model.Phys Lett A,1995,201:293-305
[15]Chau L L,Shaw J C,Tu M H.Solving the constrained KP hierarchy by gauge transformations.J Math Phys,1997,38:4128-4137
[16]Willox R,Loris I,Gilson C R.Binary Darboux transformations for constrained KP hierarchies.Inverse Problems,1997,13:849-865
[17]He J S,Li Y S and Cheng Y.Two choices of the gauge transformation for the AKNS hierarchy through the constrained KP hierarchy.J Math Phys,2003,44:3928-3960
[18]Nimmo J J C.Darboux transformations from reductions of the KP hierarchy//Makhankov V G,Bishop A R,Holm D D.Nonlinear Evolution Equations and Dynamical Systems.Singapore:World Scientific,1995: 168-177
[19]He J S,Wu Z W,Cheng Y.Gauge transformations for the constrained CKP and BKP hierarchies.J Math Phys,2007,48:113519
[20]Oevel W.Darboux transformations for integrable lattice systems//Alfinito E,Martina L,Pempinelli F. Nonlinear Physics:Theory and Experiment.Singapore:World Scientific,1996:233-240
[21]Liu S W,Cheng Y,He J S.The determinant representation of the gauge transformation for the discrete KP hierarchy.Sci China Math,2010,53:1195-1206
[22]Tu M H,Shaw J C,and Lee C R.On Darboux-Backlund transformations for the q-deformed Korteweg-de Vries hierarchy.Lett Math Phys,1999,49:33-45
[23]He J S,Li Y H and Cheng Y.q-deformed KP hierarchy and q-deformed constrained KP hierarchy.SIGMA,2006,2:060
[24]Chen H H,Lee Y C and Lin J E.On a new hierarchy of symmetry for the Kadomtsev-Petviashvili equation. Physica D,1983,9:439-445
[25]Orlov A Yu,Schulman E I.Additional symmetries for integrable systems and conformal algebra repesentation.Lett Math Phys,1993,12:171-179
[26]Adler M,Shiota T,van Moerbeke P.A Lax representation for the vertex operator and the central extension. Comm Math Phys,1995,171:547-588
[27]Dickey L A.On additional symmetries of the KP hierarchy and Sato's B¨acklund transformation.Comm Math Phys,1995,167:227-233
[28]Takasaki K.Toda lattice hierarchy and generalized string equations.Comm Math Phys,1996,181:131-156
[29]Tu M H.On the BKP hierarchy:Additional symmetries,Fay identity and Adler-Shiota-van Moerbeke formula.Lett Math Phys,2007,81:91-105
[30]He J S,Tian K L,Foerster A,Ma W X.Additional symmetries and string equation of the CKP hierarchy. Lett Math Phys,2007,81:119-134
[31]Cheng J P,Tian K L,He J S.The additional symmetries for the BTL and CTL hierarchies.J Math Phys,2011,52:053515
[32]Li C Z,He J S.Dispersionless bigraded Toda hierarchy and its additional symmetry.Rev Math Phys,2012,24:1230003
[33]Li C Z,He J S,Su Y C.Block type symmetry of bigraded Toda hierarchy.J Math Phys,2012,53:013517
[34]van Moerbeke P.Integrable fundations of string theory//Babelon O,Cartier P,Kosmann-Schwarzbach Y. Lectures on Integrable Systems.Singapore:World Scientific,1994:163-267
[35]Aratyn H,Nissimov E,Pacheva S.Virasoro symmetry of constrained KP hierarchies.Phys Lett A,1997,228:164-175
[36]Tian K L,He J S,Cheng J P,Cheng Y.Additional symmetries of constrained CKP and BKP hierarchies. Sci China Math,2011,54:257-268
[37]Shen H F,Tu M H.On the constrained B-type Kadomtsev-Petviashvili hierarchy:Hirota bilinear equations and Virasoro symmetry.J Math Phys,2011,52:032704
[38]Oevel W and Rogers C.Gauge transformations and reciprocal links in 2+1 dimensions.Rev Math Phys,1993,5:299-330
[39]Enriquez B,Orlov A Yu,Rubtsov V N.Dispersionful analogues of Benney's equations and N-wave systems. Inverse Problems,1996,12:241-250
∗Received January 8,2014;revised March 11,2015.This work is supported by the Fundamental Research Funds for the Central Universities(2015QNA43).
†Corresponding author:Jingsong HE.
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ASYMPTOTIC BEHAVIOR OF GLOBAL SMOOTH SOLUTIONS FOR BIPOLAR COMPRESSIBLE NAVIER-STOKES-MAXWELL SYSTEM FROM PLASMAS∗
- ON SOLVABILITY OF A BOUNDARY VALUE PROBLEM FOR THE POISSON EQUATION WITH A NONLOCAL BOUNDARY OPERATOR∗
- GENERAL DECAY OF SOLUTIONS FOR A VISCOELASTIC EQUATION WITH BALAKRISHNAN-TAYLOR DAMPING AND NONLINEAR BOUNDARY DAMPING-SOURCE INTERACTIONS∗
- Lp-CONTINUITY OF NONCOMMUTATIVE CONDITIONAL EXPECTATIONS∗
- CONTROLLABILITY AND OPTIMALITY OF LINEAR TIME-INVARIANT NEUTRAL CONTROL SYSTEMS WITH DIFFERENT FRACTIONAL ORDERS∗
- A MATHEMATICAL MODEL OF ENTERPRISE COMPETITIVE ABILITY AND PERFORMANCE THROUGH EMDEN-FOWLER EQUATION FOR SOME ENTERPRISES∗
