逆经验干流而上 觅数位表之演变价值

浙江慈溪市教研室（315000） 金 奎

逆经验干流而上 觅数位表之演变价值

浙江慈溪市教研室（315000） 金 奎

数位顺序表串联着整数学习的脉络。以“干流”为喻，直观形象地阐述数位顺序表演变过程中，学生积累整数学习的经验的始末。立足教材的分析与对比，捕捉到在数位顺序表、计数器、辅助图的多次无缝链接中，学生经历学表、借表、补缝、隐表、无表的压缩与释放。最终，整数学习干流中的经验不断丰盈，数位表演变价值不断突显，知识结构逐步建立牢固。

逆觅 经验干流 数位表 入海口 源头

干流指什么？在一个水系中，直接流入海洋或内陆湖泊的河流可称干流，流入干流的河流叫做支流。加以引申，“数”经验干流则是指直接影响数概念建立中各阶段的主体经验，其间众多支流可称为支经验，进而形成与河流相似的经验流。

整数是学生能亲手触摸的数，认识、大小、数位、计数、位数、取值等众多知识，都包含在压缩模型——数位顺序表中，决定它成为整数认识的经验干流。（如下图）

由图可见：大数认识之前，学生经历着长时间整数的浸润，数位顺序表串联着整数学习的脉络。其间目睹着经验干流的扩展与壮大，当经验集聚已像洪峰一样随时会“决堤而出”时，分级线成为入海口，如何平稳入海？数位顺序表经历了怎样的压缩与释放？不妨逆寻“表”的演变，探究其教学价值。

干流的入海口如何形成？

涓涓细流，汇成大海，入海的悲壮谁来识？

四年级上册“大数的认识”是学生认识整数暂告一段落的节点。其间数位顺序表在经历了“提取、抽象、压缩”后在此处悄然隐退，释放为淡淡的“印痕”——“分级线”，成为认识大数、理解大数、比较大数的核心线索和重要手段，并悄然入海。

一、学表→借表

1.四位一级的整体性认知

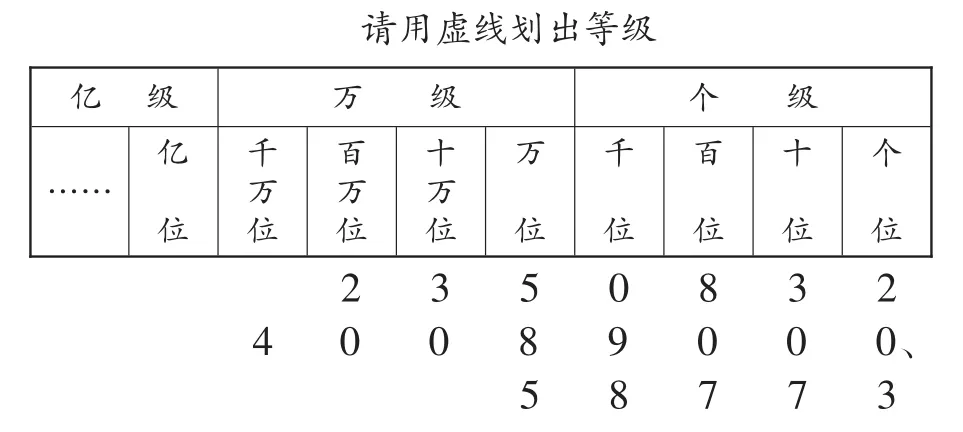
“万以上数的认识”延续原有用计数器迁移进率的经验，进一步完善数位顺序表，第一次明确概括了计数单位、数级、数位的概念，教学中可以让学生读一读、填一填加深对表的认知与记忆，使学生掌握个级包括个位、十位、百位、千位，万级包括万位、十万位、百万位、千万位，以此类推亿级的各个数位，从整体上认知“四位一级”的有序性，并体会数的无穷大。

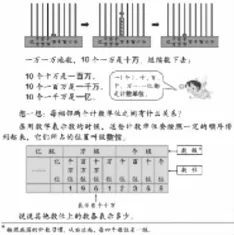
2.关键数位的占领性记忆

当学生已经熟练掌握基本知识后，可说一说：从右边起，第五位是什么位？第九位是什么位？适时点拨：记住从右边起第五位是万位，第九位是亿位。

万位和亿位作为两个“战略高地”，既是各级的转折点，也是充当了分级线演变进程中“拐杖”的角色，数的读法、写法都将借数位顺序表进行学习，教师需通过点、面结合的方式，引导学生反复操练。有了对数级的扎实掌握，数位表与分级线可共同出示：

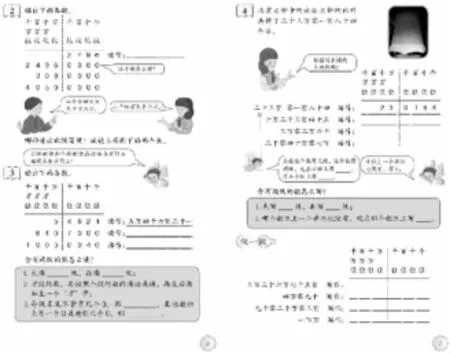
两级的数怎么读？读的时候脑中浮现的是什么？成功的学习往往是前经验的提取。在“表”与“线”的联合中，首先提取的是万以内数的读写法，为万级的读写提供经验；其次提取的是回想数级，运用分级线加上“万”字或把分级线当作“万”字写出万级上的数字。至于零的读法与补位，都与“四位一级”相关，更加说明了数位顺序表的现实意义。

3.分级线的隙中补缝

以上两图中的数位顺序表外形更为简单，但可能会打乱学生刚刚建立起来的表的具象，为了及时弥补，可跟进以下练习：

学生借助数位表中的数级直接在表下用虚线划分各级，充分感知分级线与表中数级之间的对应关系，认识与读法之间的缝隙得到填补；表与线的柔和处理使“流经之地毫无堵塞，顺利畅通”，让更多的学生体会数学前后知识之间的内在联系，学会有意识把控演变经验。

二、有表→隐表

教材从完整表到简单表，步子稳健，并以表和分级线同时呈现的方式使学生能够在显与隐的交互中掌握读写方法，但这并不是教学所要达到的最终目标，事实上数位表的隐形就是分级线，所以“有表有线”必将行进为“无表有线”。（如下表）

把万以内数的读法融入整数的体系中，这是第1题的用意。尽管只出现分级线，但要强化的是各级读法与原有读法的相通性。通过读法的前后沟通，第2题的表与线共存是对例题的回旋，“数”、“表”结合给更多学生一个思维支撑，这样让学生自己分级，自己读数变得顺理成章。第3题先通过小组交流的方式，为学生提供再学习的机会，分散难点，根据讨论达成的共识进行先分线，再读数。分线的方式很开放，可以参考课本，也可以自行发明，如“，”等，不同的学生得到不同的发展，甚至有的开始尝试想“线”读“数”。读法与写法事实上是顺与逆的辩证。如果读法教学到位，写法就会相对简单。“做一做”模仿例题“表线齐全”。而第5题已经隐去了表，但把“万”字改为红色，暗示学生回想：“万”即数位表，可以先画分级线后写出数。第6题引导学生借助计数器去表示，但学生也可以先画分级线后借助计数器去理解。有了这样的分解经验后，第7题就进行综合运用，第8题则是大数在生活中的应用。

这些读写的练习都遵循由表到隐表的思路。读数时，借助“万”字定乾坤；写数时，引导学生先画分级线再写，发挥出“表”的作用。

三、强化→弱视

分级线不断强化，数位表渐渐隐去，读数和写数有了更简洁的“眼见载体”。每见到读数或写数，学生脑中会一下子跳出分级线，说明分级线已真正成为数位表的代言。尽管亿以上数的认识（左下图）也还是从表入手进化为分级线，但事实上学生已经越过了“表”的经验，完全可以采用自学的方式进行。

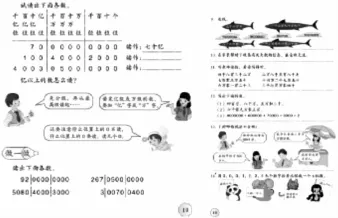
读数中学生可以自主表示分级，更重要的是“，”比虚线更为简洁，形式上更接近无线。在读数与写数的混合练习中（如右上图），教材中没有任何分级的提示，就是让学生根据自身的能力选择合理的方式，这种强化与弱视并行的“宽容”充分关注了不同的学生渡过“洪峰”的时差。

四、有形→无形

无论是“表”或是“线”，都是对整数认识的有形支撑，吻合学生认知的规律。当线的刺激由强变得越来越弱时，更多的学生也许会用心中的符号代替线，如下例取近似数时常常会在千位加“点”——借万位找千位，那么亿以上数的改写或省略则借亿位找到千万位，这已经是分级线的“变形”，也是占领性记忆的用武之地。能想到这样加“点”，其实学生已经无数次地闪现过“无线”的念头，甚至有的已用脑中“留空”或笔下“留空”的方式直接研究了。

数位顺序表这一“干流”凭借分级线的强与弱、有与无渡过洪峰般的经验涌动，实现有机提升。但这一路并不艰辛与惊险，“线”，无需做出力挽狂揽的壮举便出海，这说明原有经验对大数认识具有较强的“保驾”之力。不妨逆流而上，寻觅干流的途径与源头。

支流的汇入为哪般？

干流中流淌的经验来自于众多支流的汇入，学生的方法、能力都随着汇入更加丰富。如二年级下册的“万以内数的认识”分两部分进行，一是1000以内数的认识，二是10000以内数的认识，但两个阶段不仅仅是内容的承接，更重要的是经验的历练、方法的选取：

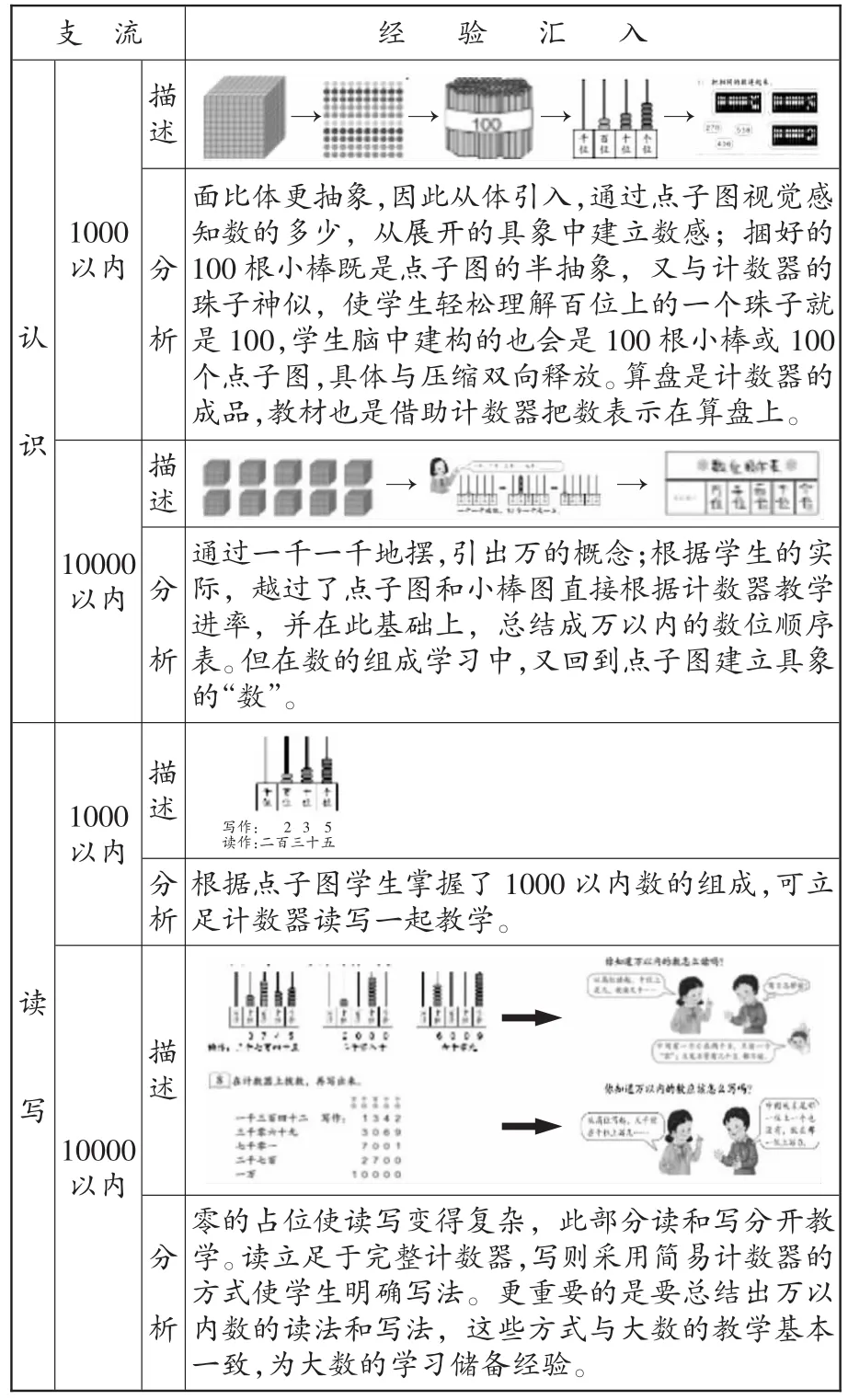
支流 经验汇入→→面比体更抽象，因此从体引入，通过点子图视觉感知数的多少，从展开的具象中建立数感；捆好的100根小棒既是点子图的半抽象，又与计数器的珠子神似，使学生轻松理解百位上的一个珠子就是100，学生脑中建构的也会是100根小棒或100个点子图，具体与压缩双向释放。算盘是计数器的成品，教材也是借助计数器把数表示在算盘上。分析→描述认识描述 分 析1000以内1000以内通过一千一千地摆，引出万的概念；根据学生的实际，越过了点子图和小棒图直接根据计数器教学进率，并在此基础上，总结成万以内的数位顺序表。但在数的组成学习中，又回到点子图建立具象的“数”。→描述写作： 2 3 5读作：二百三十五10000以内分析根据点子图学生掌握了1000以内数的组成，可立足计数器读写一起教学。读写→→➨10000以内描述 分析➨零的占位使读写变得复杂，此部分读和写分开教学。读立足于完整计数器，写则采用简易计数器的方式使学生明确写法。更重要的是要总结出万以内数的读法和写法，这些方式与大数的教学基本一致，为大数的学习储备经验。

不难看出，“1000以内数的认识”中，通过立体、面、小棒等引出计数器中的千位；在此基础上“10000以内数的认识”则把计数器抽象为大数认识前最完整的数位顺序表，并进化为简易的数位表进行写数教学，这与大数教学完全一致，“100以内的数的认识”也是如此。可见计数器是数位顺序表最接近的数学实物图，无论哪个阶段，它将成为学生理解数的组成、读写等知识的最重要载体。

干流的源头在哪里？

计数器给了整数认识强大的直观支撑与理解，学生既可以把具象的数逐步抽象成珠子，又可借眼见的珠子释放大量生活实物，那么计数器是什么时候引入教学的？干流的真正源头在哪里？

1.计数器首次出现的轻巧

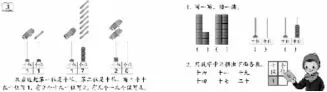
计数器在一年级上册“11～20数的读写”一课第一次正式出现，并做到了三对应（左下图）。一是借助熟知的小棒生活实物图轻巧地引出计数器这一学具实物图，学生能够感悟十位、个位与之一一对应，明白十根小棒只用十位上一颗珠子即可替代的计数原理；二是数位与数的抽象图，对应计数器十位和个位的珠子图，使“数”可在具象与抽象之间自由穿越；三是文字表述与各辅助图遥相呼应，学生可以根据“图经验”初步感知数位顺序与数的读写法，这也正是以后学习更大数的策略与方式。为了突出计数器对于数认识的作用，教材（右下图）加强了计数器“展开式”与“压缩式”的对比练习，突破十位上一颗珠子的“事实数量”就是十块方格的难点；计数器毕竟只是数位表的过渡，因此第2题又据“表”建“位”，帮助学生读数与写数。

2.辅助图多层次的丰羽

小棒不仅是生活实物也是学具实物，成为计数器的原形完全符和儿童理解数学的认知规律。其实在零起点教学时，学生已经紧紧依靠这些辅助图学习数了。

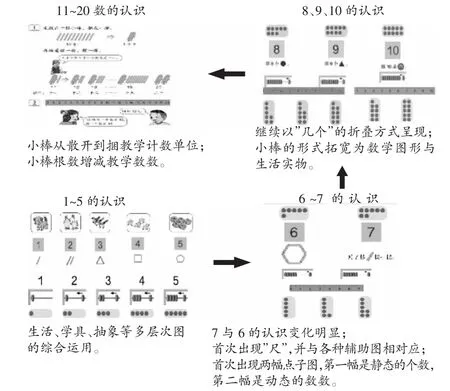
1～5的认识突出了生活实物图与学具实物图（如小棒、算珠）等的结合，然后抽象为数学意义的点子图，多种辅助使数学“有血有肉”。从顺逆两方面分析可以看出“6、7的认识”成为数启蒙认识中的纽带：“6”承接了1～5以“展开小棒根数”为主的呈现方式，但隐去了生活实物图，而“7”首次以“折叠的几根”去摆一摆，引导学生自己去创造“多少”，并把这一方式延续给8、9、10的认识。因此，“20以内数的认识”整个过程已出现多层次数的认识辅助手段，为计数器的产生、数位表的壮大、分级线的演变等积累了丰富的活动经验和推理经验，能让学生在整数学习的“河道”里根据自身认知水平去自由游弋。由此看来干流的源头，就在步入认识“1”的那一刻。

结语

当我们从分级线这一入海口逆干流而上，找到源头的那份期待越发迫切；当我们顺流而下，一路感受着各个阶段中学生对于数的认识日益深刻的那份喜悦：执著中经历了从生活实物图、学具实物图，到数学实物图、数学抽象图等支流经验的积累过程，逐步实现计数器与顺序表的无缝对接；然而干流越来越宽广，越来越充盈时，却只化为一缕细线，纵身汇入数的大海……

（责编 金 铃）

G623.5

A

1007-9068（2015）11-017