Vortex interactions between forewing and hindwing of dragonfly in hovering flight
2015-11-21ChunMeiXieWeiXiHuang
Chun-Mei Xie,Wei-Xi Huang∗
aSino-French Engineer School,Beijing University of Aeronautics and Astronautics,Beijing 100191,China
bAML,Department of Engineering Mechanics,Tsinghua University,Beijing 100084,China
Vortex interactions between forewing and hindwing of dragonfly in hovering flight
Chun-Mei Xiea,b,Wei-Xi Huangb,∗
aSino-French Engineer School,Beijing University of Aeronautics and Astronautics,Beijing 100191,China
bAML,Department of Engineering Mechanics,Tsinghua University,Beijing 100084,China
A R T I C L E I N F O
Article history:
Received 21 November 2014
Accepted 31 December 2014
Available online 14 February 2015
Vortex interaction
Dragonfly
Hovering flight
Immersed boundary method
Two tandem flapping wings in viscous flow were modeled by using the immersed boundary method for exploration of the aerodynamics of dragonfly in hovering flight.Interaction between the forewing and the hindwing,and its effect on the lift forces,were examined by varying the phase difference of the wing motions and the inter-distance of the two wings.Two vortex interaction modes were identified at different phase differences and inter-distances,which give rise to significant variations of the lift forces. The first interaction mode increases the lift of the forewing and the second one enhances the lift of the hindwing.The two modes occur at different time during a flapping period and have different influence on the lift of wings as the phase difference varies.
©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
During the past several decades,studies have been carried out extensively on the aerodynamic performance and flow physics of insect flight[1-4].As a four-winged insect,dragonfly possesses the ability of controlling their flight performance by modulating the stroke amplitude,frequency and angle of attack of each wing.The aerodynamic interaction of the wings induces more complexities ofthe flight mechanism[5-9].Froma kinematic study on live dragonflies,Alexander[10]observed that the offset in the flapping motion between the forewing and the hindwing played a significant role in their flightperformance.Azuma and Watanabe[11]pointed out that dragonflies modulated the forewing and hindwing phasing rather than the flapping frequency,according to their flight velocity,i.e.the hovering or cruise status.Furthermore,Thomas et al.[12]proposed mechanisms related to the generation of highlift leading edge vortices and the interaction between forewing and hindwing in the flight of dragonfly.They also claimed that two-dimensional(2D)simulation is able to present the main features of interaction.Maybury et al.[13]investigated experimentally the wing-wake interaction in dragonflies and evaluated in more details the functional significance of stroke-phase modulation on wake structure,aerodynamic force generation and lift-todrag ratio.They also found that the inter-distance of the two wings has a significant influence on the aerodynamic interaction between the two wings.Based on the experimental observations,numerical studies have been rising in recent years due to the fast increase of computation power.Wang[14]proved that the lift generated by a 2D hovering insect is enough to support its weight.Wang and Russell[15]showed that the in-phase flapping generates the maximum lift force and is beneficial for takeoff,while the out-of-phase flapping requires nearly the minimal energy consumption to obtain the required lift force in hovering flight.They also provided a simple model for explaining the interaction of the two wings with different phase lags,which neglects the real interaction of vortices shed from the forewing and the hindwing.Moreover,Isogai et al.[16]performed three-dimensional(3D)simulations of flow around tandem wings and obtained the total lift force and necessary power.Rival et al.[17]simulated a 2D dragonfly model and mainly focused on the difference of vortices around the hindwing and those around a single wing.In brief,the phase lag between the forewing and the hindwing is the main distinctive feature for the dragonfly flight,but the underling aerodynamic mechanism has not been fully understood despite that some efforts have been made on this problemas mentioned above.In the presentstudy,we take the two tandem flapping wings in viscous flow as a 2D model ofthe dragonfly in hovering flight.Variations ofthe liftforces under different kinematic configurations are examined,and are analyzed by disclosing the vortex interactions between the forewing and the hindwing.
A 2D wing model is set as an ellipse shape with the aspect ratio of0.1.The kinematics ofboth the forewing and the hindwing are in the same form with a phase difference,based on the experimental measurements[14,15].The center displacements and the angles of attack of the forewing and the hindwing are governed by
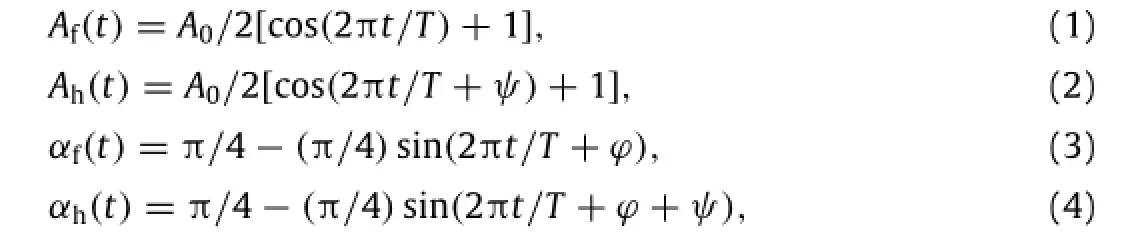
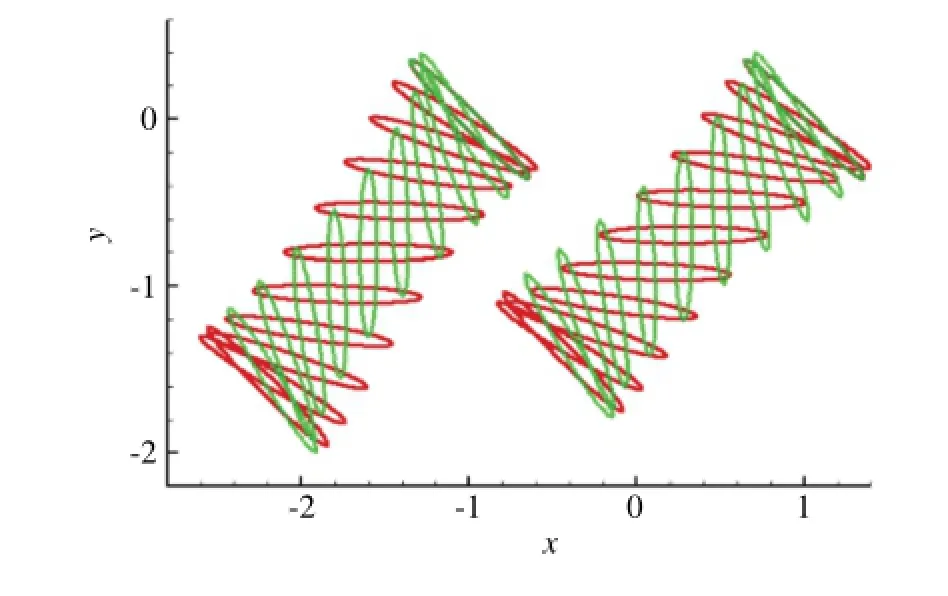
Fig.1.Positions of the forewing and the hindwing during a flapping period for ψ=0◦and d=2.The downstroke phase is indicated by red and the upstroke phase by green.(For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.)
where A0isthe stroke amplitude,ϕis the phase difference between the wing center displacement and the angle of attack,ψis the phase difference between the motions of the forewing and the hindwing,and the subscripts‘‘f''and‘h''denote the forewing and the hindwing respectively.In the presentstudy,the parametersare similar to the single wing case[14],i.e.A0=2.5,T=7.85,and ϕ=0◦in the dimensionless form.Here we use the chord length and the maximum center velocity as the characteristic length and velocity,respectively.The stroke planes are inclined at different angles for the forewing and the hindwing,i.e.βf=53◦andβh= 44◦according to Wang and Russell[15].In the simulations,we fix the kinematics of the forewing and change the initial state of the hindwing to obtain different phase lags(ψ)and inter-distances of the two stroke planes(d),which are varied in the ranges of 0◦≤ψ≤360◦and 1.6≤d≤2.4,respectively.A schematic of the two flapping wings is plotted in Fig.1 for the case ofψ=0◦and d=2.
In order to simulate the flow around the flapping wings,the incompressible Navier-Stokes and continuity equations are solved by the fractional step method in a staggered Cartesian grid system[18].The immersed boundary method is adopted to enforce the noslip condition on the wings'surfaces,which is capable of solving flow over complex geometries while retaining the efficiency of the original flow solver based on the regular mesh.Details and validations ofthe numericalmethod can be found in our previous studies[19,20].The Reynolds number based on the chord length and the maximum flapping velocity is set to be 157 as in Wang[14].The size ofthe computationaldomain is 8×8,and 1024×1024 grids are used to uniformly discretize the domain.The computational time step is 0.000785,which results in a CFL number of about 0.1,and a flapping cycle is divided into 104steps.It should be pointed out that the influence of the computational domain boundary is not fully eliminated by using the current domain size,but the difference in vortex characters around the wings is negligible with those in a larger domain,which is the main focus of the present study. Moreover,the computational results of the second flapping period is adopted for analysis in the following.Although aerodynamic forces on the wings have not been converged at the second period,the vortex interactions of the tandem flapping wings have formed,which remain essentially the same as those at a later period.
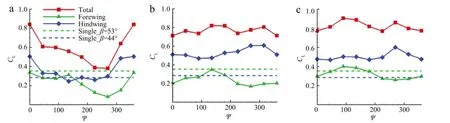
Fig.2.Variations of the mean lift coefficients with the phase difference:(a)d=1.6,(b)d=2.0,(c)d=2.4.The results of the single wing flapping in the same inclined stroke planes are also included for comparison.

Fig.3.Time histories of the lift coefficients of(a)the forewing and(b)the hindwing for differentψand d=1.6.
Figure 2 shows the variations of the mean lift coefficients(CL)with the phase differenceψfor three different inter-distances,i.e.d=1.6,2.0,2.4,while the results ofthe single wing flapping inthe same inclined stroke planes are also included for comparison. We can see that the lift coefficients are less varied withψas d increases.Although for the single wing case CLofβf=53◦is higher than that ofβh=44◦,for the tandem two flapping wings CLof the hindwing is generally higher than that of the forewing,because of the vortex interactions ofthe two wings as willbe discussed below. For d=1.6(Fig.2(a)),the results are similar to Wang and Russell[15].The liftofthe hindwing reaches its maximumatψ=0◦and is nearly independent of the phase difference whenψ∈[45◦,275◦]. The lift of the forewing also shows obvious dependence onψ,indicating the significant interaction of the two wings.As d increases to d=2.0 and d=2.4(Figs.2(b)and 2(c)),similar trends of the lift variations are observed for the two cases.The lift of the forewing is maximal atψ=135◦and that of the hindwing is maximal atψ=270◦.Unlike the d=1.6 case,the total lift is not maximal atψ=0◦,mainly due to the difference in the lift of the hindwing.
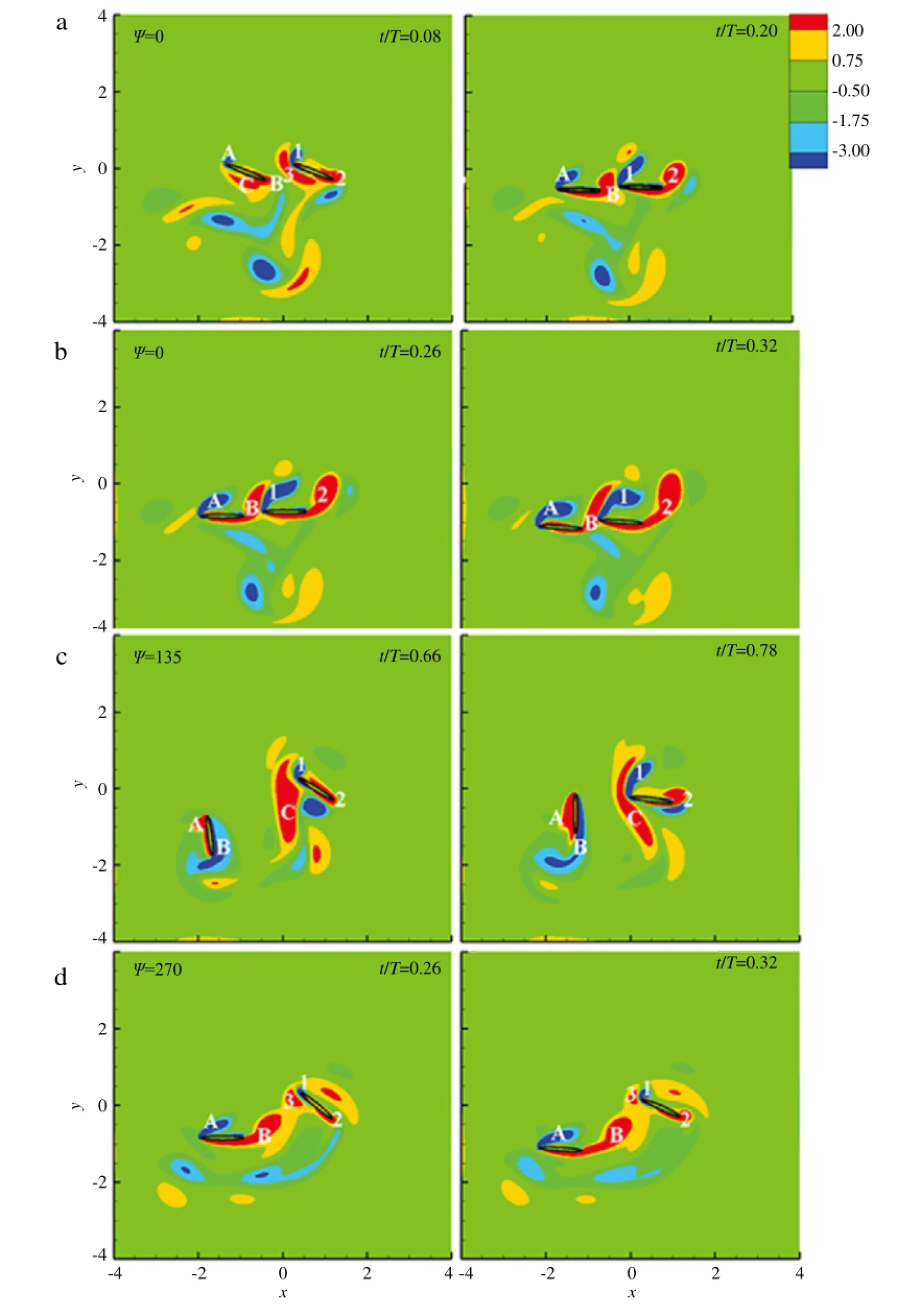
Fig.4.Contours of vorticity around the flapping wings at the instants near the lift peaks of(a)the hindwing withψ=0◦,(b)the forewing withψ=0◦,(c)the hindwing withψ=135◦,and(d)the forewing withψ=270◦.
To see the effect ofthe phase difference,time histories ofthe lift coefficients of both the forewing and the hindwing are plotted in Fig.3 for differentψand d=1.6,together with the results of the single wing case,and vorticity contours around the flapping wings at the instants near the lift peaks in the time histories are displayed in Fig.4.It is seen in Fig.3 that the shape of the single wing case is consistent with that of Wang's[14],with two peaks during the downstroke.An inspection of the flow field indicates that the first peak is generated by wake capture,while the second one is caused by the variationofangle ofattack.Interestingly,the second peak lift of both the forewing and the hindwing are enhanced as compared with thatofthe single wing case,as a resultofthe interaction ofthe two wings.As shown in Fig.3(b),the high CLof the hindwing with ψ=0◦can be explained by a long duration of high lift in a period. At t/T=0.08 and t/T=0.20,two peaks in CLare observed,and the corresponding vorticity fields are seen in Fig.4(a).At t/T=0.08,the hindwing crosses its own wake vortex generated during the previous upstroke(vortex 3),a mechanism called wake capture[1].The second peak at t/T=0.20 is mainly caused by the interaction between the forewing and the hindwing.Meanwhile,the forewing's lift is also growing to a peak value(Fig.3(a)).At this time(Fig.4(b)),the trailing edge vortex of the forewing(vortex B)is shedding,and the leading edge vortex of the hindwing(vortex 1)is moving towards vortex B.As a result,vortex B can not be shed normally,and instead it is attached to the forewing,which increases the lift force of the forewing and is referred to as the first interaction mode in the following.Interaction with vortex B also makes vortex 1 attached to the hindwing,and then weakens the new leading edge vortex,which increases the lift of the hindwing and is referred to as the second interaction mode in the following.
Atψ=135◦,the mean lift of the hindwing is minimal(Fig.2(b)),since the duration of the lift peak is much shorter than theψ=0◦case(Fig.3(b)).The vorticity fields at the instants near the lift peak are shown in Fig.4(c).We can see that the hindwing captures the wake vortices produced during the previous upstroke,but the wing-wing interaction is negligible because the distance of two wings is far.Thus,the high lift status is not durable,unlike theψ=0◦case.On the other hand,the mean lift of the forewing is minimal atψ=270◦(Fig.2(c)),due to the low peak value of CL(Fig.3(a)).Similarly,the vorticity fields at the instants near the lift peak are shown in Fig.4(d).Compared to theψ=0◦case(Fig.4(b)),the interaction between the two wings affects the trailing edge vortex of the forewing(vortex B)differently.As seen in Fig.4(d),the vortex B is tilted by the upstroke motion of the hindwing,resulting in a reduced lift peak value.

Fig.5.Time histories of the lift coefficients for d=2.0 and(a)ψ=0◦,(b)ψ=135◦,(c)ψ=270◦.

Fig.6.Contours of vorticity around the flapping wings at the instants near the lift peaks of(a)both wings withψ=0◦,(b)the forewing withψ=135◦,(c)the hindwing withψ=135◦,(d)the forewing withψ=270◦,and(e)the hindwing withψ=270◦.The legend of the vorticity contours is the same as that in Fig.4.
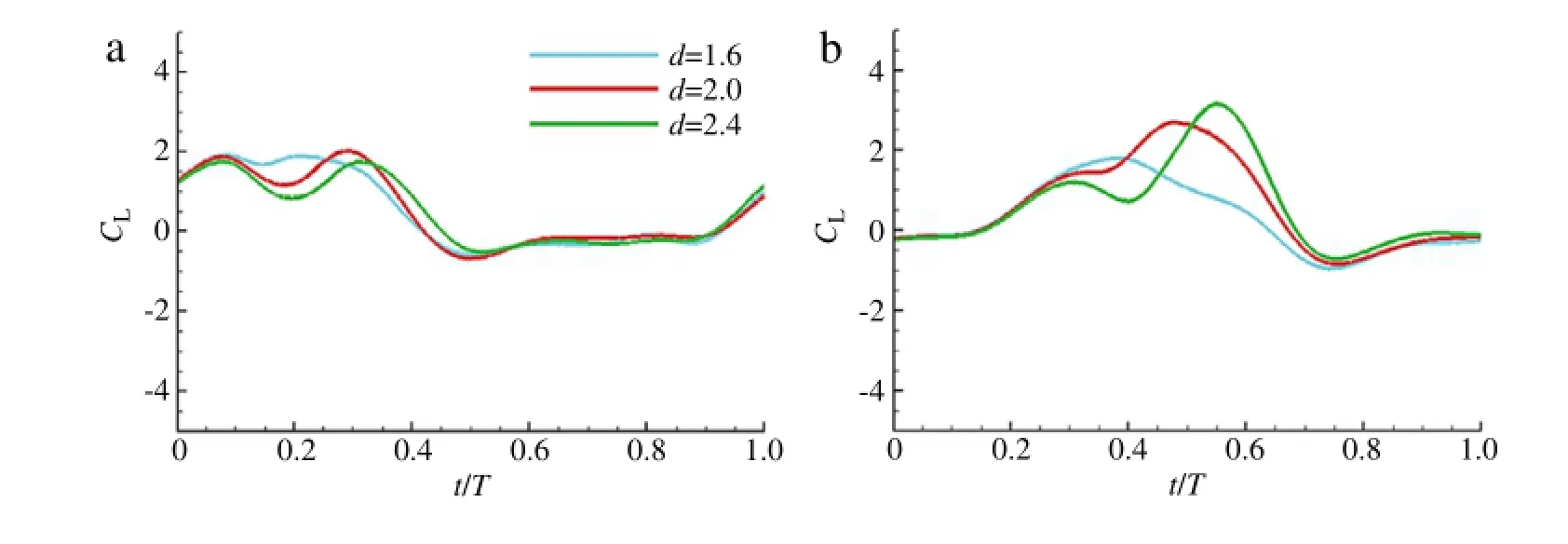
Fig.7.Time histories of the lift coefficient of the hindwing at(a)ψ=0◦and(b)ψ=270◦for three different inter-distances between the two wings.
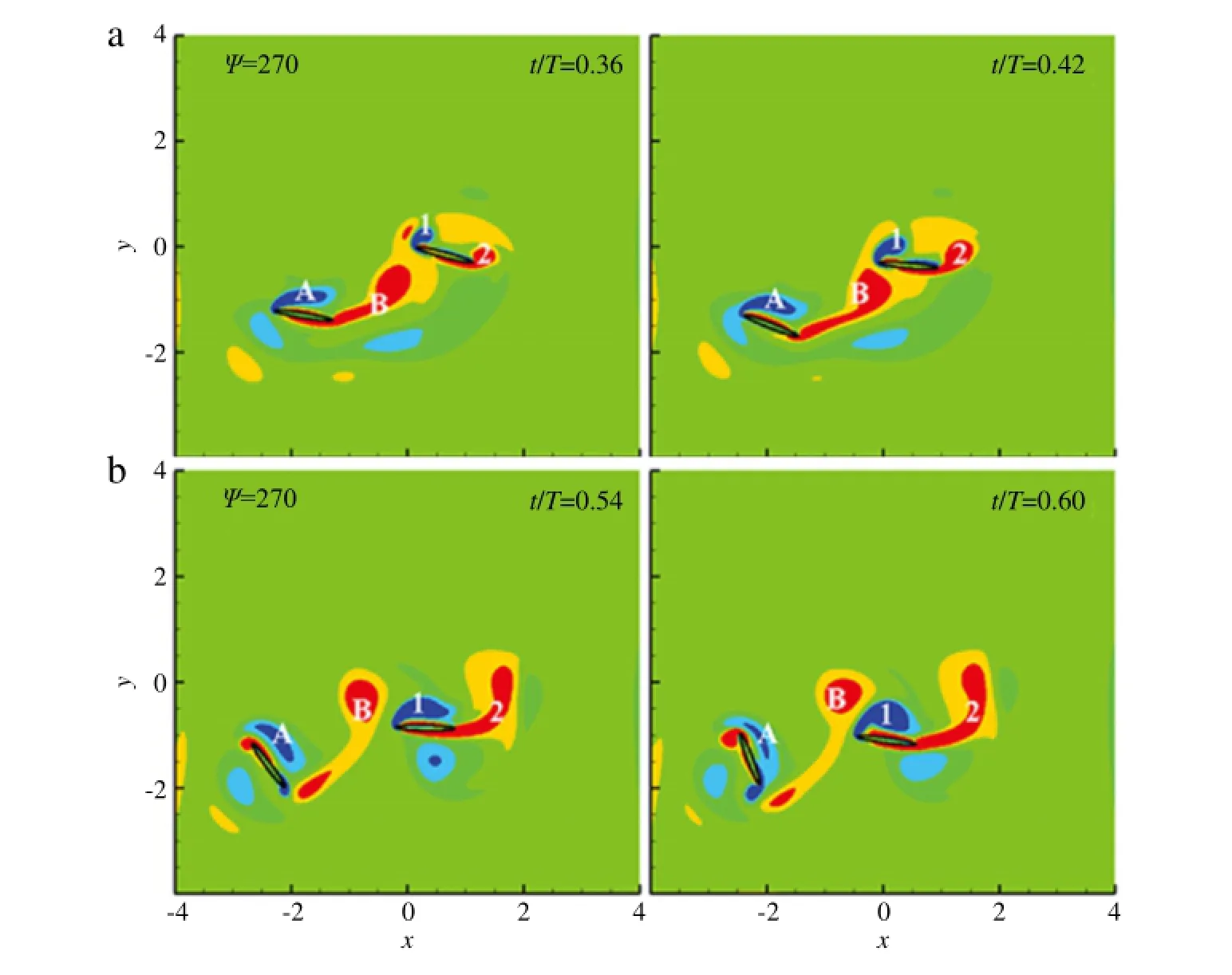
Fig.8.Contours of vorticity around the flapping wings at the instants near the lift peaks of the hindwing forψ=270◦and(a)d=1.6,(b)d=2.4.The legend of the vorticity contours is the same as that in Fig.4.
As d increases to 2.0 and 2.4(Figs.2(b)and 2(c)),the difference in the lift coefficients of the two wings is minimal atψ=135◦due to the maximal CLof the forewing,but is maximal atψ=270◦due to the maximal CLof the hindwing.To see more clearly,time histories of CLof the d=2.0 case are plotted in Fig.5 for these two phase differences as well asψ=0◦.As shown in Fig.5(b),CLof the forewing forψ=135◦is the largest at about t/T=0.1,while that of the hindwing forψ=270◦reaches maximum at about t/T=0.5.The vorticity fields at the instants near the lift peak at the three phase differences are then examined.Figure 6(a)shows the interaction between the two wings when they are in phase,corresponding to the second peak in Fig.5(a).Here we do not show the first peak because the wake capture appears in all three cases of different d,and we mainly focus on the interaction between the two wings.Figure 6(b)shows the interaction of the two wings at the instants near the lift peak of the forewing forψ=135◦.At this time,the trailing edge vortex of the forewing(vortex B)and the leading edge vortex of the hindwing(vortex 1)move in the opposite directions,which enhances vortex B and is the main reason of the increase of CLofthe forewing.We also callitthe firstinteraction mode.From Fig.6(c)it is seen that the maximal CLof the hindwing forψ=135◦is caused by the interaction between the trailing edge vortex of the forewing(vortex C),which is almost completely shed,and the leading edge vortex of the hindwing(vortex 1).It is the second interaction mode but is stronger than theψ=0◦case,where we see half of vortex C is combined to the trailing edge vortex of the hindwing(vortex 2).It enhances vortex 2 and causes the increase of CLof the hindwing.Atψ=270◦(Fig.6(d)),the interaction mode corresponding to the lift peak of the forewing is similar to theψ=135◦case(Fig.6(b)),but is less distinctive.The interaction mode corresponding to the lift peak of the hindwing in Fig.6(e)is also similar toψ=135◦case(Fig.6(c)),but the trailing edge vortex of the forewing(vortex C)affects more the hindwing. Moreover,in Fig.6(e),the hindwing is almost horizontally moving downward,which is also a reason for the larger lift of the hindwing than theψ=135◦case(Fig.6(c)).We also checked other phase differences of the two wings,it was found that these two interaction modes are always present,but the first mode is most distinctive atψ=135◦and the second one atψ=270◦.For d=2.4,the interaction modes are similar to the d=2.0 case andare not shown here.Recall that for the d=1.6 case,both the first and second interaction modes are most significant atψ=0◦.So the optimal phase difference is dependent on the inter-distance of the two wings.Nevertheless,the interaction modes remain similar before diminishing as the inter-distance becomes large.
A comparison of Figs.2(a),2(b)and 2(c)shows that the interdistance affects more the lift of the hindwing than the forewing. Thus,time histories of CLof the hindwing atψ=0◦andψ=270◦with three different inter-distances are plotted in Fig.7.Atψ=0◦(Fig.7(a)),CLof the hindwing is close for the three distances.The most obvious difference occurs at the beginning of the flapping cycle.The wake capture and the interaction of the two wings occur closely in time for d=1.6,which causes the longer duration of high lift.In Fig.7(b),the lift of the d=1.6 case is much lower than the other two cases.This phenomenon is caused by the impact of the trailing vortex of the forewing on the hindwing.As shown in Fig.8,the vorticity field corresponding to the lift peak of the hindwing for d=1.6 is compared with that for d=2.4.For d=1.6,Fig.8(a)shows that the hindwing hits the trailing vortex of the forewing(vortex B)before it is completely shed.On the contrary,for d=2.4(Fig.8(b)),the hindwing passes the shedding trailing edge vortex(vortex B),which interacts with the leading edge vortex of the hindwing(vortex 1).As a result,a higher lift peak of the hindwing is formed for the larger d atψ=270◦.
Aerodynamics of two tandem flapping wings in viscous flow were simulated as a 2D model of dragonfly in hovering flight by using the immersed boundary method.Interaction between the forewing and the hindwing were examined by varying the phase difference of the wing motions and the inter-distance of the two wings.The results indicate that the interaction of the two wings is significant under certain kinematic conditions.As the interdistance increases,the lift coefficients of the forewing and the hindwing,and thusthe totalliftforce,are less varied with the phase difference.By examining the vorticity fields around the flapping wings,several mechanisms were disclosed for the explanation of the lift enhancement by the vortex-vortex or vortex-wing interaction.The wake capture is always present regardless of the inter-distance.The first interaction mode was identified for the increase of the lift of the forewing by affecting the forewing's trailing edge vortex.It was then shown that the second interaction mode is more complex and is caused by the interaction of the forewing's trailing edge vortex and the leading and trailing edge vortices of the hindwing,which can substantially increase the lift of the hindwing.The interaction of the two wings affects more the hindwing than the forewing on their aerodynamic performances.
This work was supported by the National Natural Science Foundation of China(11322221)and Tsinghua University Initiative Scientific Research Program(20131089267).
[1]M.H.Dickinson,F.O.Lehmann,S.P.Sane,Wing rotation and the aerodynamic basis of insect flight,Science 284(1999)1954-1960.
[2]J.M.Birch,M.H.Dickinson,Spanwise flow and the attachment of the leadingedge vortex on insect wings,Nature 412(2001)729-733.
[3]S.P.Sane,The aerodynamics ofinsectflight,J.Exp.Biol.206(2003)4191-4208.
[4]M.Sun,Insect flight dynamics:stability and control,Rev.Modern Phys.86(2014)615-645.
[5]J.M.Wakeling,C.P.Ellington,Dragonfly flight I.Gliding flight and steady-state aerodynamic forces,J.Exp.Biol.200(1997)543-556.
[6]J.M.Wakeling,C.P.Ellington,Dragonfly flight II.Velocity,accelerations and kinematics of flapping flight,J.Exp.Biol.200(1997)557-582.
[7]J.M.Wakeling,C.P.Ellington,Dragonfly flight III.Lift and power requirements,J.Exp.Biol.200(1997)583-600.
[8]S.B.Savage,B.G.Newman,D.T.B.Wong,The role of vortices and unsteady effects during the hovering flight of dragonflies,J.Exp.Biol.83(1979)59-77.
[9]K.Isogai,S.Fujishiro,T.Saitoh,M.Yamashaki,M.Matsubara,Study on aerodynamic mechanism of hovering flight of dragonfly by using a robot,in: Proceedings of ISABMECH2003,Tokai Univ.Pacific Center,Honolulu,HI,Paper S.3-02,2003.
[10]D.E.Alexander,Unusual phase relationships between the forewings and hindwings in flying dragonflies,J.Exp.Biol.109(1984)379-383.
[11]A.Azuma,T.Watanabe,Flight performance of a dragonfly,J.Exp.Biol.137(1988)221-252.
[12]A.L.R.Thomas,G.K.Taylor,R.B.Srygley,R.L.Nudds,R.J.Bomphrey,Dragonfly flight:free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms,controlled primarily via angle of attack,J.Exp.Biol.207(2004)4299-4323.
[13]W.J.Maybury,F.O.Lehmann,The fluid dynamics of flight control by kinematic phase lag variation between two robotic insect wings,J.Exp.Biol.207(2004)4707-4726.
[14]Z.J.Wang,Two dimensional mechanism for insect hovering,Phys.Rev.Lett.85(2000)2216-2219.
[15]Z.J.Wang,D.Russell,Effect of forewing and hindwing interaction on aerodynamic forces and power in hovering dragonfly flight,Phys.Rev.Lett. 99(2007)148101.
[16]K.Isogai,S.Fujishiro,T.Saitoh,M.Yamamoto,M.Yamasaki,M.Matsubara,Unsteady three-dimensional viscous flow simulation of a dragonfly hovering,AIAA J.42(2004)2053-2059.
[17]D.Rival,D.Schonweitz,C.Tropea,Vortex interaction of tandem pitching and plunging plates:a two-dimensional model of hovering dragonfly-like flight,Bioinsp.Biomin.6(2011)016008.
[18]K.Kim,S.J.Baek,H.J.Sung,An implicit velocity decoupling procedure for incompressible Navier-Stokes equations,Int.J.Numer.Methods Fluids 38(2002)125-138.
[19]W.X.Huang,S.J.Shin,H.J.Sung,Simulation of flexible filaments in a uniform flow by the immersed boundary method,J.Comput.Phys.226(2007)2206-2228.
[20]S.J.Shin,W.X.Huang,H.J.Sung,Assessment of regularized delta functions and feedback forcing schemes for an immersed boundary method,Int.J.Numer. Methods Fluids 58(2008)263-286.
∗Corresponding author.
E-mail address:hwx@tsinghua.edu.cn(W.-X.Huang).
*This article belongs to the Fluid Mechanics
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Adjoint-based optimization of flapping plates hinged with a trailing-edge flap
- Numerical simulation of unsteady flows over a slow-flying bat
- Propulsive performance of two-and three-dimensional flapping flexible plates
- Learning from bat:Aerodynamics of actively morphing wing
- A coupled immersed boundary-lattice Boltzmann method and its simulation for biomimetic problems
- A modified criterion for wave-induced momentary liquefaction of sandy seabed
