Learning from bat:Aerodynamics of actively morphing wing

Yongliang Yu，Ziwu Guan

The laboratory for Biomechanics of Animal Locomotion，University of Chinese Academy of Sciences，Beijing 100049，China

Learning from bat:Aerodynamics of actively morphing wing

Yongliang Yu∗，Ziwu Guan

The laboratory for Biomechanics of Animal Locomotion，University of Chinese Academy of Sciences，Beijing 100049，China

A R T I C L E I N F O

Article history：

Received 21 November 2014

Received in revised form

26 December 2014

Accepted 4 January 2015

Available online 14 February 2015

Bat flight

Morphing wing

Lift

Thrust

Different from birds and insects，bats have complex wing-deformation capacity to generate high aerodynamic forces.In flight，the actively morphing of bat wing includes the twisting from wing root to wing tip，the cambering along the chordwise direction，the bending along the spanwise direction and the wing area-changing caused by the stretch and retraction of the wingspan.It was found that the high thrust and lift required in bat flight are dependent on the wing twisting and cambering respectively.Moreover，the integrated wing-morphing generates the aerodynamic lift and thrust mainly during the downstroke and almost negligible forces during the upstroke.The wing area-changing and bending can be used to amplify the positive forces in the downstroke duration and reduce the negative forces in the upstroke duration.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

In order to fly forwards，a flying animal must flap its wings to generate lift and thrust to balance the weight and drag，respectively.However，bats，especially moderate and small bats，have different flight features from birds and insects.For example，if a mature pigeon（body length is about 25 cm）flies at a speed of 15 m/s，the chord-based Reynolds number is greater than 105and the required lift coefficient（CL）is about 0.47 which is easy to be obtained by wings with a low angle of attack（AOA）.The thrust is generated by the flapping wings with a frequency of 1-2 Hz.The quasi-steady aerodynamics has been successfully used to study the bird flight in the latter part of the last century［1］.When we consider the insect flight，the flapping flight mode changes a lot.A fruit fly beats its wings with a very high frequency（about 100 Hz）and a high AOA（about 30°-40°）to generate enough lift and thrust in its hovering or forward flight（＜1 m/s）.The strongly unsteady flow is the main feature to overcome the viscous effects which restrict the high lift and thrust generation in the traditional conditions as the flight Reynolds number is as low as 100［2，3］，and the wings' pronation and supination（wing pitching at the ends of upstroke and downstroke）in the strokeplane are very important to produce high forces［4］.Whether birds or insects，the deformation of their wings can be ignored when we investigate the main mechanisms of high aerodynamic forces generation.In contrast，for bats，the actively wing-deforming plays an important role，although largescaled bats can glide and fly like birds.For a moderate bat flight（Leptonycteris yerbabuenae，a nectar feeding species），the characteristic speed is about3-5 m/s，and the flapping frequency is about 10 Hz.The Reynolds number is in the range of 104-105.The values of these parameters locate in between those of birds and insects，and the required lift coefficient is as high as 2.6 according to the experimental data［5］.Therefore，in bat flight，besides the flapping mechanisms，new mechanisms due to the specialwing-body structure attract more and more researchers to study.

A bat wing which consists of flexible muscularized membrane and upper limbs attaches all the lateral border of the body，from the neck to the ankle［6］.This arrangement limits the bat-wing pronation and supination which have been widely investigated in insect flapping flight.The AOA at the root，equal to the body tilt angle，changes slightly during the wing stroke，and it is estimated around 7°based on the experimental data［5，7］.A fixed wing with an aspect ratio 3（the characteristic aspect ratio of a bat wing）at this AOA can only generate a small lift（CL≈0.62）and a drag（CD≈0.12）which can not supportthe bat weightin forward flight. If a rigid wing flaps like a bird，the averaged lift and drag in a cycle increase simultaneously.When the flapping amplitude is close to 40°（the stroke amplitude is about 80°），the lift and drag are about 0.80 and 0.19 respectively［8］.Therefore，it has been suggested that the actively wing-morphing is a significant way to generate the high lift and thrust required in bat forward flight.

In fact，the large active wing-deformation has been observed widely and measured in the studies of bat flight.The Swartz group［9］did a systematical research in bat flight.They revealed that，the wing motion is quite complex when a batflies atrelatively slow speeds.They also quantified the complexity of bat wing kinematics［10］.Busse et al.［5］gave details of the three dimensional wingbeat kinematics including wing movement，frequency，stroke plane angles，angles of attack，wing camber in the section of the fifth digit，etc.However，the aerodynamic mechanisms of the bat wing morphing have not been clearly explained.Norberg［11］had a preliminary study on the aerodynamic forces in slow horizontal flight（2.35 m/s）for a long-eared bat based on the steady-state aerodynamic and momentum theories，but Hedenström et al.［12］pointed out that the unsteady effects cannot be ignored.The aerodynamic effects of the wing-deforming have not been considered until Wang et al.［13］and Guan and Yu［8，14］built the morphing models in bat flight.

As is well-known，during the whole stroke，the bat upper limb with the wing muscles makes the flexion and extension of the elbow，the abduction and adduction of the wrist.These actions lead to the wing deformation along the spanwise and chordwise directions［6］.First，the AOA at the wing tip is varying with time and its time-averaged value is not equal to that of the root AOA mentioned above.The variation of the AOA distribution from the wing root to the wing tip is called‘twisting''（sketched in Fig.1（a））.Second，the variation of wing camber along the chordwise direction is controlled by the bending digits who stretch the flexible muscularized membranes，and we call it‘cambering''（Fig.1（b））.Third，it is found thata bat bends its wings along the spanwise direction more during the upstroke than the downstroke.This wing deformation with time is called‘bending''（Fig.1（c））.Last，it is found simultaneously that the area of the bat wing is changing rhythmically with the flapping.The area increases（or decreases）when the wingspan is stretched（or retracted）by the upper limb，and it is obvious that the wingspan is larger during the downstroke than the upstroke. This process is called wing‘area-changing''（Fig.1（d））.

How to model the actively deforming bat-wing？In our studies［8，14］，the four morphing models were proposed with mathematic expressions and all of the related parameters were determined according to the experimental data［5］.The flapping motion with respect to the angular movementis almost sinusoidal. The twisting deformation is defined as the linearly distributed AOA from the wing root to the tip，and the AOA of the wing tip follows a simple harmonic motion.The cambering deformation of the wing along the chordwise direction is regarded as an arc with its arch rise changing periodically.Similarly，the bending deformation along the spanwise direction is modeled by the arc-shaped surface.And the area-changing deformation depends on the wingspan（arc length）stretching sinusoidally，while the change of the chord length is ignored.

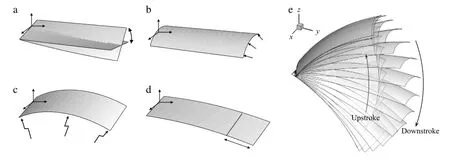
Fig.1.（a）Wing-twisting sketch，（b）wing-cambering sketch，（c）wing-bending sketch，（d）wing area-changing sketch，and（e）the flapping configuration of the integrated wing-morphing（right wing），where the incoming flow is along the x direction.

A morphing plate of aspect ratio 3 is used to model a bat wing and a three dimensional unsteady panel method has been developed to predict the aerodynamic forces generated by the flapping model-wing with the leading edge separation.The integrated wing-morphing during a flapping cycle is shown in Fig.1（e）where the twist，camber and wingspan in the downstroke duration（0＜t/T≤0.5）are significantly different from those in the upstroke duration（0.5＜t/T≤1.0）.Furthermore，the forces generated by the integrated morphing model-wing（including twisting，bending，cambering，and area-changing）are shown in Fig.2.It is found that the lift and the thrust are mainly generated during the downstroke and they are very small during the upstroke.The mean lift is 3.09 and the mean thrust is 0.32.Obviously，the morphing wing can produce a large enough lift to balance the bat weight（the required lift is 2.6）and a sufficient thrust to propel bat flight forward against the drag.

Now，what can we learn from bat？In order to answer this question，we compared the aerodynamic forces generated by the elementary morphing models with the rigid flapping wing model one by one.（1）The twisting wing can not only enhance the timeaveraged lift but also decrease its fluctuation during the whole stroke.Especially，it can generate the thrust which is required in the forward flight during both the downstroke and the upstroke［8］.（2）The cambering wing can greatly increase the lift but change the mean drag little.The bigger the basic camber is，the higher the lift curve is elevated in the whole cycle.It is interesting that the cambering wing can also generate the thrust during downstroke though the drag is presented during upstroke［14］.（3）The wing-bending along the spanwise direction can also enhance the mean lift but a small increase of the drag.It mainly reduces the minus lift and the drag in the upstroke duration，relative to the rigid wing-flapping［14］.（4）The wing area-changing shows the same effects as the wing-bending，but in the downstroke duration the lift is increased a lot［14］.

Furthermore，the force generation mechanisms ofeach elementary morphing model have been discussed comprehensively in our studies［8，14］.（1）Ithasbeen proved thatthe twisting motion in bat flight has the same function as the pronation and supination in insect flight which has been investigated widely in the last decades. The twisting motion can modulate the vortex shedding by increasing the amplitude of the trailing-edge，so that the high thrust is generated and at the same time the lift is also enhanced.（2）The cambered wing has the asymmetric effects which result in the high lift generation，since the effective AOA is increased during the downstroke and decreased during the upstroke.（3）The aerodynamic mechanism of the wing bending and area-changing is anamplifier effect.As mentioned above，during the downstroke，the high lift is generated by the cambering wing and the high thrust is generated by the twisting，so the larger the wing area is，the larger forces required in flight are obtained.During the upstroke，the smaller the wing area is，the smaller the negative lift and the drag are.The area-changing model realizes the regulation directly，and the bending model regulates the projected wing-area and makes it smaller during upstroke than downstroke.Additionally，the added mass effects and vortex effects were analyzed.It was found that the added mass effects have no contribution to the mean forces for a morphing wing in a flapping cycle.That means the vortex control is a key factor to generate the high aerodynamic forces.

In short，we have learned preliminarily the aerodynamics of actively deforming wing in batforward flight:the higherthrustand liftare dependenton the appropriate incrementofthe amplitude of the wing-twisting and wing-cambering，respectively，and they can be enhanced synchronously by the wing area-changing or bending. Furthermore，there are some further issues to be studied step by step，such as the vortex control mechanisms，the optimization of the combined deformation，and even the passive deformation effects.So we will learn a lot from bats.

This work was supported by the National Natural Science Foundation of China（10602061 and 11372310）.

Fig.2.The lift and drag generated by the integrated morphing wing during a whole stroke，where the time-averaged liftis 3.09 and the thrustis 0.32.

［1］G.K.Taylor，M.S.Triantafyllou，C.Tropea（Eds.），Animal Locomotion，Springer-Verlag，Berlin Heidelberg，2010.http://dx.doi.org/10.1007/978-3-642-11633-9.

［2］Y.L.Yu，B.G.Tong，H.Y.Ma，An analytic approach to theoretical modeling of highly unsteady viscous flow excited by wing flapping in small insects，Acta Mech.Sin.19（2003）508-516.http://dx.doi.org/10.1007/BF02484543.

［3］Y.L.Yu，B.G.Tong，A flow control mechanism in wing flapping with stroke asymmetry during insect forward flight，Acta Mech.Sin.21（2005）218-227. http://dx.doi.org/10.1007/s10409-005-0032-z.

［4］M.Sun，J.Tang，Unsteady aerodynamic force generation by a model friut fly wing in flapping motion，J.Exp.Biol.205（2002）55-77.

［5］R.von Busse，A.Hedenström，Y.Winter，L.C.Johansson，Kinematics and wing shape across flight speed in the bat，Leptonycteris yerbabuenae，Biology Open. 1（2012）1226-1238.http://dx.doi.org/10.1242/bio.20122964.

［6］J.W.Bahlman，S.M.Swartz，K.S.Breuer，Design and characterization of a multiarticulated robotic bat wing，Bioinspiration and Biominetics 8（2013）016009. http://dx.doi.org/10.1115/smasis2013-3190.

［7］M.Wolf，L.C.Johansson，R.von Busse，Y.Winter，A.Hedenström，Kinematics of flight and the relationship to the vortex wake of a Pallas'long tongued bat（Glossophaga soricina），J.Exp.Biol.213（2010）2142-2153. http://dx.doi.org/10.1242/jeb.029777.

［8］Z.W.Guan，Y.L.Yu，Aerodynamic mechanism of forces generated by twisting model-wing in bat flapping flight，Appl.Math.Mech.（English Ed.）35（2014）1607-1618.http://dx.doi.org/10.1007/s10483-014-1882-6.

［9］S.M.Swartz，J.Iriarte-Diaz，D.Riskin，X.D.Tian，A.Song，K.Breuer，Wing structure and the aerodynamic basis of flight in bats，in:45th AIAA Aerospace Sciences Meeting and Exhibit，Jan.8-11，Reno，Nevad，2007. http://dx.doi.org/10.2514/6.2007-42.

［10］D.K.Riskin，D.J.Willis，J.Iriarte-Diaz，T.L.Hedrick，M.Kostandov，J.Chen，D.H. Laidlaw，K.S.Breuer，S.M.Swartz，Quantifying the complexity of bat wing kinematics，J.Theoret.Biol.254（2008）604-615. http://dx.doi.org/10.1016/j.jtbi.2008.06.011.

［11］U.M.Norberg，Aerodynamics，kinematicsand energetics ofhorizontalflapping flight in the long-eared bat Plecotus auritus，J.Exp.Biol.65（1976）179-212.

［12］A.Hedenström，L.C.Johansson，M.Wolf，R.von Busse，Y.Winter，G.R.Spedding，Batflightgenerates complex aerodynamic tracks，Science 316（2007）894-897. http://dx.doi.org/10.1126/science.1142281.

［13］S.Z.Wang，X.Zhang，G.W.He，T.S.Liu，Lift enhancement by dynamically changing wingspan in forward flapping flight，Phys.Fluids 26（2014）061903. http://dx.doi.org/10.1063/1.4884130.

［14］Z.W.Guan，Y.L.Yu，A study on aerodynamics and mechanisms of elementary morphing models for flapping wing in bat forward flight，Appl.Math.Mech.（English Ed.）（2014）in press.arXiv:1403.6824.

∗Corresponding author.

E-mail address：ylyu@ucas.ac.cn（Y.Yu）.

*This article belongs to the Fluid Mechanics