一类非线性差分方程的全局渐进稳定性*

赵玉萍

（青海民族大学数学与统计学院，青海　西宁　810007）

一类非线性差分方程的全局渐进稳定性*

赵玉萍

（青海民族大学数学与统计学院，青海西宁810007）

非线性差分方程在工程技术中有广泛应用.笔者利用特殊不等式，研究了一类非线性差分方程解的稳定性，得到了这类方程有全局渐进稳定平衡点的充分条件，给出了方程唯一的正的全局渐进稳定的平衡点.改进了N.kruse和T.Nesemann已有的研究结果.通过一个例子说明了主要结论，使差分方程的研究领域更广、更完善.

稳定性；差分方程；非线性

0　引言

差分方程在计算机科学、经济学、生物数学等领域有着广泛的应用，差分方程的研究越来越受到人们的重视.近几年，关于差分方程的稳定性理论的研究，引起了国内外学者的广泛关注，成果较多[1－16].在文献[2]中N.kruse和T.Nesemann研究了差分方程

渐进稳定性.笔者研究一类普遍的非线性差分方程

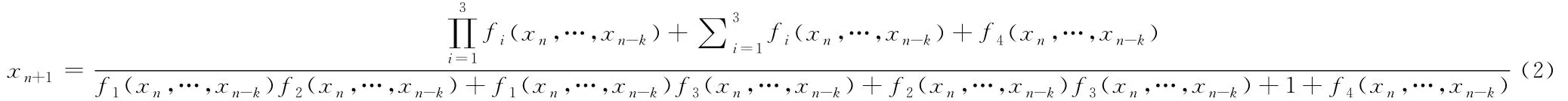
正解的稳定性.

1　引理

2　主要结果

[1]Agarwal.R.P.Difference Equations and Inequalities[M].Theory，Methods，and Applications，2nd ed，Monographs and Textbooks in Pure and Applied Mathematics Vol.228，Marcel Dekker，New York，2000.

[2]N.kruse and T.Nesemann.Global asymptotic stability in some discrete dynamical systems[J].Math.Anal.Appl.，1999，235：151－158.

[3]Shi.B，Wang.Z.C and Yu.J.S.Asymptotic constancy of solutions of linear parabolic Volterra difference equations[J].Comput.Math.Appl. 2006，32：65－77.

[4]Morchalo.J.On convergence of solutions of a second order nonlinear difference equations[J].Appl.Math.Comput.2003，12：59－66.

[5]X.Li.Global behavior for a fourth－order rational difference equation[J].Math.Anal.Appl.2005，312：555－563.

[6]X.Li.Qualitative properties for a fourth－order rational difference equation[J].Math.Anal.Appl.2005，311：103－111.

[7]R.P.Agarwal，C.Cuevas，H.Soto，M.El－Gebeily.Asymptotic periodicity for some evolution equations in Banach spaces[J].Nonlinear Anal. 2011，74：1769－1798.

[8]A.Caicedo，C.Cuevas，G.M.Mophou，G.M.N'Guérékata.Asymptotic behavior of solutions of some semilinear functional differential and differential equations with infinite delay in Banach spaces[J].Franklin Inst.2012，349：1－24.

[9]X.H.Nang，Y.Liu.Bounded oscillation for second－order delay difference equations with unstable type in a critical case[J].Appl.Math.Lett. 2003，16：263－268.

[10]X.H.Nang，J.S.Yu.Oscillations of delay difference equation in a critical state[J].Appl.Math.Lett.2000，13（20）：9－15.

[11]Qiong Meng，JurangYan.Bounded oscillation for second－order nonlinear neutral differential equations in critical and non－critical states[J]. Journal of Computational and Applied Mathematics，2008，211：156－172.

[12]C.Cuevas，C.Lizama.Almost asymptotic solutions to a class of semilinear fractional differential equations[J].Appl.Math.Lett.2008，21：1315－1319.

[13]G.Papaschinopoulos，C.J.Schinas.Oscillation and asymptotic stability of two systems of difference equations of rational form[J].Differ.Equ. Appl.2001（7）：601－617.

[14]L.Del Campo，M.Pinto，C.Vidal.Almost and asymptotically almost periodic solutions of abstract retarded functional difference equations in phase space[J].Differ.Equ.Appl.2001，17（6）：915－934.

[15]S.Stevic'.Global stability of a max－type equation[J].Appl.Math.Comput.2010，216：354－356.

[16]G.Papaschinopoulos，C.Schinas，V.Hatzifilippidis.Global behavior of the solutions of a max－equation and of a system of two max－equations[J].Comput.Anal.Appl.2003，5（2）：237－254.

[责任编辑 苏 琴] [责任校对 方丽菁]

Global Asymptotic Stability for a Family of Nonlinear Difference Equations

ZHAO Yu－ping
（Department of Mathematics and Statistics，Qinghai University for Nationalities，Xining810007，China）

Nonlinear difference equations are widely used in engineering technology.By means of special inequality technique，this paper is concerned with stability of solution for a family of nonlinear difference equations，sufficient conditions that the equations have globally asymptotically stable equilibrium were given，an only positive globally asymptotically stable equilibrium was given，which improves some known results that N.kruse and T.Nesemannt had studied.An example is given to illustrate the main results.The research field of difference is wider，more perfect.

Stability；Difference equation；Nonlinear

O175.7

A

1673－8462（2015）02－0055－04

2014－11－25.

国家自然科学基金资助项目（11361047）；青海民族大学校级科研项目.

赵玉萍（1975－），女，青海湟中人，硕士，青海民族大学数学与统计学院副教授，研究方向：差分方程，微分方程的理论研究.