微熵率算法分析及实证研究
2015-11-19黄奕谢维波
黄奕,谢维波
(1.华侨大学 计算机科学与技术学院,福建 厦门361021;2.华侨大学 厦门软件园嵌入式技术开放实验室,福建 厦门361008)
在时间序列的分析中,决定序列的可观测因素很多,且相互作用的动力学方程往往是非线性的.20世纪80年代以来,由于Takens对Whitney早期在拓扑学方面工作的发展,使得深入分析时间序列的背景和动力学机制成为可能.在确定性的基础上对序列动力学因素的分析,目前广泛采用的是相空间重构法.微熵率法是Gautam 等提出的一个基于样本时间序列及其替代数据的相空间重构方法[1].熵率是指随机源(1个随机过程)随时间变化的平均不确定性;1个随机过程的熵率是该过程平均每产生1个随机变量其不确定度大小的度量.微熵率法中的替代数据方法为iAAFT.iAAFT 是一种性能稳定的替代数据产生方法,能很好匹配原始数据的傅里叶幅度谱和概率密度分布,在数据的非线性检验中被广泛采用.本文以Henon map混沌系统为数据源,以Henon map混沌特性的理论为依据,实证研究微熵率算法的各个环节.
1 Henon map混沌系统
1976年,Michel Henon给出了Henon map混沌系统[2-3].此后,许多学者就Henon map混沌系统的全局结构进行数值与仿真研究,并将Henon map系统扩展到更高维[4].

图1 Henon混沌序列Fig.1 Henon chaotic sequence
1.1 Henon混沌序列
Henon混沌序列为

式(1)中:a,b为系统参数;d为系统延迟.当a=1.4,b=0.3时,系统具有混沌特性.经过足够多次的迭代,Henon序列呈现“混沌”现象.
Henon混沌序列(d=1),如图1所示.图1中:对应初值为(x0=0.4,x1=0.6)和(x0=0.4+10-8,x1=0.6)的Henon混沌序列利用Matlab仿真的情况(实验均采用Matlab完成).大约在0<k<40的范围内,xk序列基本一致;当k>40之后,初始值微小扰动(10-8)的两组xk序列呈现急剧的差异,体现了混沌序列“初值敏感性”的特征.
1.2 Henon map奇异吸引子
奇异吸引子是混沌运动的主要特征.令

由式(1),(2)可得

式(2),(3)构成了Henon map混沌系统[5].点集(xk,yk)组成一条不封闭的曲线,即Henon map混沌系统的奇异吸引子相图.
图1两种序列的奇异吸引子相图,如图2所示.由图2可知:两种序列几乎“完全重合”.尽管图1两种序列存在急剧的差异,点集(xk,yk)却呈现“相同的轨迹”.显然,由图1可知:对应点出现的“顺序”是不同的,但是轨迹却几乎“完全重合”.奇异吸引子给出的“确定性轨迹”,体现了Henon map混沌系统的稳定性,奠定了混沌系统发展规律的研究基础.

图2 Henon map混沌系统奇异吸引子相图Fig.2 Henon map chaotic system attractor
2 替代数据
为实现时间序列分析的统计学检验,时间序列需要足够多样本.样本的获取,可通过构造产生时间序列的系统,或者直接构造时间序列本身.后者产生时间序列样本的方法,称为替代数据法[6].替代数据能够尽可能精确地复制原始数据的性质(包括时间概率分布和自相关函数),但同时又是尽量随机的.
2.1 AAFT生成算法
振幅调节傅里叶变换(AAFT)有以下4个步骤[7].
步骤1原始数据{x0n},排列序号{rank0n},当x0n是{x0n}中第k小时,rank0n.
步骤2高斯白噪声{g0},按{rank0n}重排得{g′n}.
步骤3对{g′n}傅里叶变换和相位随机化处理,得序列{s′n}.
步骤4求{s′n}的排列序号{ranksn},原始数据{x0n}按{ranksn}重排得替代数据{sn}.
替代数据{sn}是原始数据{x0n}的重排,保证了替代数据与原始数据有相同的时间概率分布.因此,也有一样的均值方差等一、二阶统计量.替代数据{sn}的随机性体现在高斯白噪声{gn},及其傅里叶变换的相位随机化处理.
然而,原始数据功率谱密度(自相关函数)的性质被改变了,因为发生在步骤2和步骤4的两个重排在严格意义上不是彼此的逆操作.这种差异导致替代数据的功率谱密度在原始数据的基础上被白化.二者的差异程度取决于原始数据的时间概率分布与高斯分布的相似程度,简而言之,AAFT 算法适用于类高斯分布的时间序列.
2.2 iAAFT生成算法
为了解决AAFT 替代数据的功率谱白化问题,1996年Schreiber提出了AAFT 迭代生成算法(iAAFT).iAAFT 是一种性能稳定的替代数据产生方法,能很好匹配原始数据的傅里叶频谱和概率密度分布,在数据的统计学检验中被广泛采用.具体有以下4个步骤[8].
步骤1原始数据{x0n},排列序号{rank0n},傅里叶变换的幅度值|Xk|,计算AAFT 替代数据{sn}.
步骤2记{sn}傅里叶变换Sk=|Sk|exp(jφ(k)),保持相位不变,幅度值用|Xk|代替,得S′k=|Xk|exp(jφ(k)).
步骤3对S′k进行傅里叶反变换得{s′n},再按{rank0n}重排得{s″n}.
步骤4重复步骤2,3,直至所得数据{s″n}和原始数据有相近的功率谱密度.
确保{s″n}和原始数据的统计性质(时间概率分布、功率谱密度)趋于一致,该算法有两个基本假设.
1)步骤2对傅里叶变换幅度值的矫正,造成时间概率分布的扭曲都比上一次迭代的小.
2)步骤3的重排,造成功率谱密度的扭曲都比上一次迭代的小.
Schreiber等[7]证明:对于非线性自相关过程,替代数据的功率谱将会逐渐趋近原数据的功率谱.
3 微熵率法确定时间序列最佳嵌入参数
3.1 微熵率法
时间序列可观测性的决定因素很多,其相互作用的动力学方程往往是非线性的,甚至是混沌的.同时,计算的复杂性、有限的测量精度,以及可能存在的本质上的非确定性等多方面困难,严重制约着人们对时间序列内在机制的理解.20世纪80年代,Takens[9]对Whitney早期在拓扑学方面工作的发展,为深入分析时间序列的背景和动力学机制奠定基础.在确定性的基础上,对序列动力学因素的分析,目前广泛采用的是延迟坐标状态空间重构法(相空间重构法)[10].一般来说,非线性系统的相空间可能维数很高,甚至无穷,在大多数情况下维数并不知道.
对于给定的时间序列,相空间重构法表明存在一个最优的嵌入维数m和时延τ.如果τ太小,为了使m·τ覆盖(大于)“捕捉信号的动力学性质所需的最小时间距”,m将变得相当大;相反,如果τ大于最佳值,模型的性质将变得太离散,导致捕捉不到信号的动力学性质.Gautama等提出基于样本时间序列及其替代数据的微熵率方法,用于确定相空间的最佳嵌入维数m和时延τ.
3.2 微熵率法详细步骤
微熵率法有以下4点详细步骤[1].
步骤1原始数据{x(k)∶k=1,2,…,N},计算其Ns组替代数据,记为

步骤2嵌入维数m和时延τ的相空间.原始数据的相空间为

相空间的状态向量记为

替代数据的相空间(共Ns个),即

相空间的状态向量记为

其中:X(k)和Xs,i(k)又称为延迟矢量,延迟矢量的个数为M=N-(m-1)τ.
步骤3基于原始数据及其替代数据,确定原始数据{x(k)∶k=1,2,…,N}的熵率为

其中:I(m,τ)=H(x,m,τ)/(H(xs,i,m,τ))i.由原始数据构成的相空间,其熵为
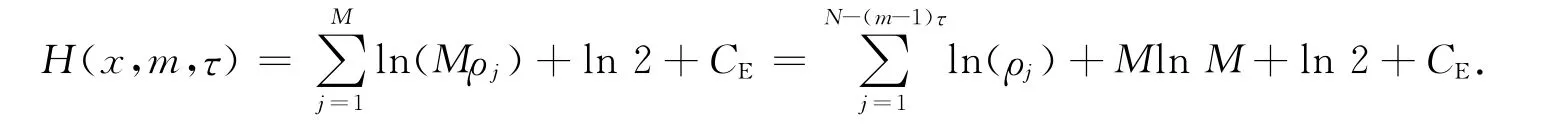
其中:欧拉常数CE=0.577 2;ρj是第j个延迟矢量与其最近邻点的欧氏距离,即

相应有
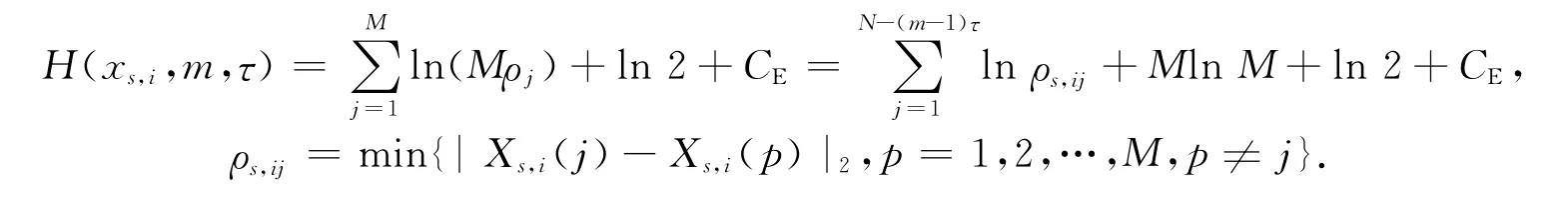
由Ns组替代数据构成的Ns个相空间,其平均熵为可见,熵率体现为原始数据相空间的熵与Ns个替代数据相空间平均熵之比.
步骤4计算Rent(m,τ)的最小值,相应的m和τ即最佳嵌入维数mopt和时延τopt.
4 数值实验
4.1 实验数据的选取
Henon序列混沌特性的理论结果:当a=1.4,b=0.3时,式(1)具有混沌特性,其参数d为时间延迟,对应最佳嵌入时延τopt.
不当的初值选择会造成式(1)的发散,分别选取两组初值以验证Henon序列混沌特征的稳定性.经过足够多次的迭代,Henon序列才会进入“稳定的”混沌状态[11].取Henon序列10 000个数据后的500个作为数据源,才得出“稳定的”结果.
4.2 实验结果
Henon序列的时延d=4,初值取(x0=0.2,x1=0.6x2=0.4,x3=0.3,x4=0.1,x5=0.5,x6=0.8,x7=0.7)和(x0=0.2+10-8,x1=0.6,x2=0.4,x3=0.3,x4=0.1,x5=0.5,x6=0.8,x7=0.7),生成两组上述的数据源(N=500)应用微熵率法分别求最佳嵌入维数mopt和时延τopt.其中:Ns的选取,以(H(xs,i,m,τ))i趋于稳定为准,文中取Ns=10.
图3,表1,2对应d=4的Henon序列.图3和表1对应的初值取(x0=0.2,x1=0.6,x2=0.4,x3=0.3,x4=0.1,x5=0.5,x6=0.8,x7=0.7)的结果.表2对应的初值取(x0=0.2+10-8,x1=0.6,x2=0.4,x3=0.3,x4=0.1,x5=0.5,x6=0.8,x7=0.7)的结果.从表1,2可以看出:m=3,τ=4时,熵率Rent(m,τ)均取得最小值,即最佳嵌入维数mopt=3和时延τopt=4(对应d=4),实证了不同的初值下Henon序列混沌特征的稳定性.
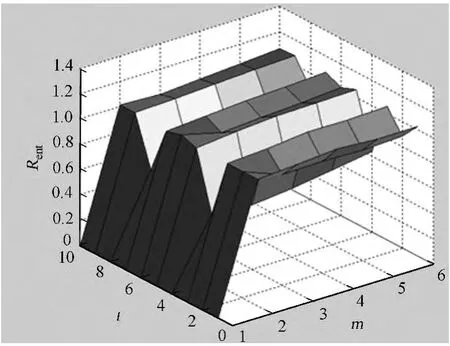
图3 Rent(m,τ)三维示意图Fig.3 3D-diagram of Rent(m,τ)
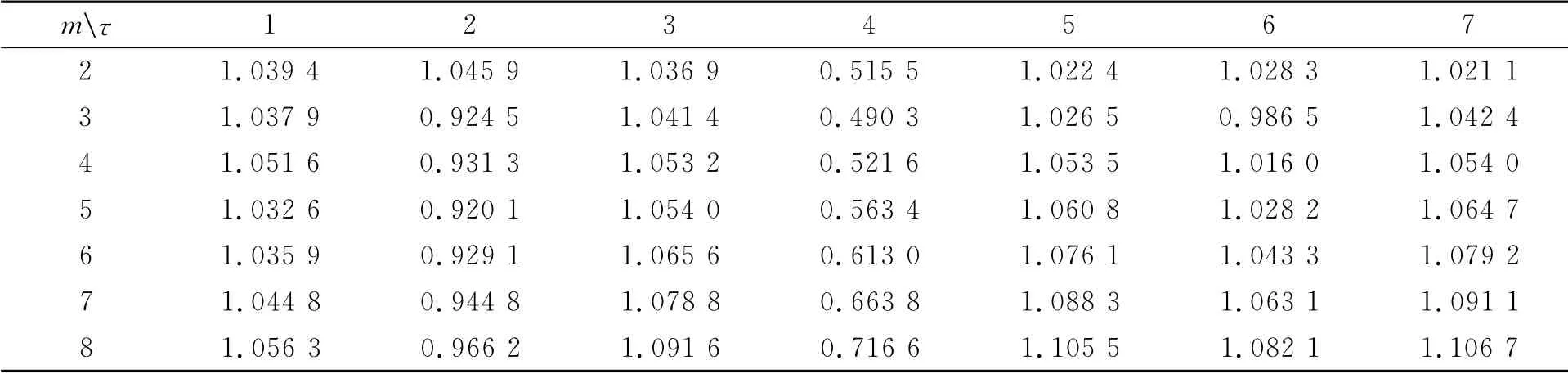
表1 第一组初值对应的RentTab.1 Rentof the first set initial value

表2 第二组初值对应的RentTab.2 Rentof the second set initial value
对应Henon序列的不同时延d,表3给出基于微熵率的辨识结果(初值取[0,1]的随机数),包括mopt,τopt,Rent(mopt,τopt).由表3可知:mopt的值恒为3,τopt的值始终与d保持一致;有效地验证了Henon序列混沌特征的稳定性,这种稳定性奠定了混沌系统的研究基础.

表3 不同时延的微熵率法辨识Tab.3 Differential entropy of different time delay
[1]GAUTAMA T,MANDIC D P,VANHULLE M M.A differential entropy based method for determing the optimal embedding parameters of signal[C]∥Processing of the Int Conf on a Coustics,Speech and Signal Processing.Hong Kong:[s.n.],2003:29-32.
[2]王光义,郑艳,刘敬彪.一个超混沌Lorenz吸引子及其电路实现[J].物理学报,2007,56(6):3113-3120.
[3]GALLAS J A C.Structure of the parameter space of the Hénon map[J].Physical Review Letters,1993,70(18):2714.
[4]HENON M.A two dimensional mapping with stranger attractor[J].Commun Math Phys,1976,50(1):69-77.
[5]BENEDICKS M,CARLESON L.The dynamics of the Henon map[J].Annals of Mathematics.1991,163(3):749-841.
[6]THEILER J,EUBANK S,LONGTIN A,et al.Testing for nonlinearity in time series:The method of surrogate data[J].Physica D:Nonlinear Phenomena,1992,58(1):77-94.
[7]SCHREIBER T,SCHMITZ A.Improved surrogate data for nonlinearity tests[J].Physical Review Letters,1996,77(4):635.
[8]KEYLOCK C J.Constrained surrogate time series with preservation of the mean and variance structure[J].Physical Review E,2006,73(3):036707.
[9]王海燕,盛昭瀚.混沌时间序列相空间重构参数的选取方法[J].东南大学学报:自然科学版,2000,30(5):113-117.
[10]TAKENS F.Detecting strange atractors in turbulence[J].Lecture Notes in Mathematics,1982,898(12):198-366.
[11]GRASSBERGER P,KANTZ H,MOENIG U.On the symbolic dynamics of the Hénon map[J].Journal of Physics A:Mathematical and General,1989,22(24):5217.
