圆盘反应器流场数值模拟
2015-11-18戴干策
邓 斌,戴干策
华东理工大学化学工程联合国家重点实验室,上海 200237
圆盘反应器起源于1900年Weigand 提出的生物转盘,早期主要应用于生物废水处理,20世纪初用于合成纤维聚酯。近年来,圆盘接触器在中低粘物系中的应用颇受关注,包括光催化[1]、柠檬酸生产[2]和精细化工[3]等领域。旋转圆盘接触器的基本结构是光滑平面圆盘,部分浸没于液体中,通过电机驱动水平轴带动垂直圆盘旋转,以此区别于垂直轴带动完全浸没于液体中的水平圆盘。水平圆盘反应器物料从中心加入,流量是预先给定的,这类流动已经有比较详细的研究。部分浸没的垂直圆盘,盘面膜厚及圆盘持液量则取决于流体物性、圆盘尺寸及旋转速度等因素,称为自计量流。从液膜流体动力学角度而言,其显著的特点是物体从液体中穿过,形成自由面,带动流体运动,而非物体作潜体运动。这类研究最早可以追溯到上世纪40年代Landau 等[4]平板抽出模型的经典工作,其后为开发涂布技术,有相当广泛的涂布流研究,主要探索抽出速度和膜厚的关系。
Landau 等[4]通过简化Navier-Stokes 方程最早提出了平板抽出模型,得到了平板带动液膜的厚度与流速和物性的关系,但当抽出速度较大时,关系式明显偏离实验结果。White 等[5]考虑了重力因素对膜厚的影响。Groenveld[6]系统研究了影响平板膜厚的各个因素,指出平板液膜厚度主要取决于物系粘度和平板抽出速度。Bintanja 等[7]研究圆盘反应器氧气传递特性时受到Groenveld 的启发,用线速度代替平板速度得到了圆盘反应器平均膜厚公式,但当转速较高时,膜厚与线速度的关系并非文中提出的线性关系。Zhevalkink 等[8]根据平板抽出模型,结合圆盘反应器忽略离心力和毛细管力的影响,并考察了液位对膜厚的影响,简化Navier-Stokes 方程并求解,得到了圆盘表面平均膜厚关系式。Zhevalkink的结果在低转速(6~33 r/min)下与实验吻合的较好,因而得到了较广泛的应用,但是当转速较高时误差较大。Vijayraghvan 等[9]利用膜厚测量仪研究了不同转速、不同物系下圆盘表面的膜厚分布,指出圆盘上液膜厚度的不均匀性,膜厚随着半径的增加而增加,实验还发现各点膜厚随转速的增加先增加再减小。Afanasiev 等[10]针对圆盘反应器从槽内带上液体的三维现象,通过有限元方法求解四阶非线性偏微分方程得到了圆盘表面液膜的分布规律,建立了二维模型,这种模型一定程度上反映了圆盘表面液膜厚度的变化规律。杨晓宇等[11]采用流体体积函数模型,对垂直旋转圆盘反应器的流动和成膜特性进行数值模拟,并考察了圆盘转速和反应器内液位高度对膜厚分布规律的影响。
关于圆盘反应器液相流型,有两个经典模型:Batchelor[12]流型与Stewartson[13]流型。王良生等[14]通过实验研究发现,在一定的粘度和转速范围内,盘间距对流型有显著的影响。Fujie 等[15]通过类比生物转盘与连续搅拌釜得到了圆盘反应器功率的相关影响因素,并将功率数与Re数相关联。
本研究尝试用计算流体力学方法,通过流体体积函数(VOF)模型考察流场,揭示流型、速度分布特征,在此基础上分析宏观特性如轴功率和平均膜厚,探讨盘间距、盘与壁面距离等因素的影响。
1 计算方法和模型验证
根据圆盘反应器内气液两相的流动特点和接触方式,采用Hirt 等[16]提出的VOF 模型进行计算。计算中将圆盘和轴表面的边界设置为旋转壁面,壁面边界条件为无滑移,自由面通过求解VOF 模型方程得到。采用Gambit 进行网格划分,ANSYS FLUENT 商业软件进行求解。圆盘反应器网格划分和计算区域均为六面体网格,为了减少网格数,节约计算时间,根据圆盘两侧流场关于圆盘对称的特点,只计算圆盘一侧的流场区域,另一侧流场采用对称边界条件获得。具体计算方法和模型验证参见作者另一篇关于圆盘反应器表面更新数值模拟的研究[17]。
2 结果与讨论
2.1 流场分析
2.1.1 圆盘表面液膜速度分布
对半径R为150 mm 的圆盘,μ为1 000 mPa·s,圆盘转速N为90 r/min 进行数值模拟,研究圆盘表面液膜的速度分布。以网格内液相体积分数为0.99 的等值面作为液膜自由面,即气液接触面。速度矢量分布如图1所示,根据速度差异可以将圆盘表面分为三个区:起始区,加速区,匀速区。液体从槽体内的静止状态到随圆盘转动必然存在着加速过程。在膜厚方向(z方向)壁面边界无滑移,圆盘转动带动内层液体运动;由于粘性力作用,内层液体通过动量交换使外层流体加速,形成加速区;随着外层流体速度增加,z方向速度梯度减小,流体内摩擦力减小,加速度减小,最后匀速,形成匀速区。(在本研究所有的流场图中,x方向表示水平方向,-y方向表示重力方向,z方向表示膜厚方向。)
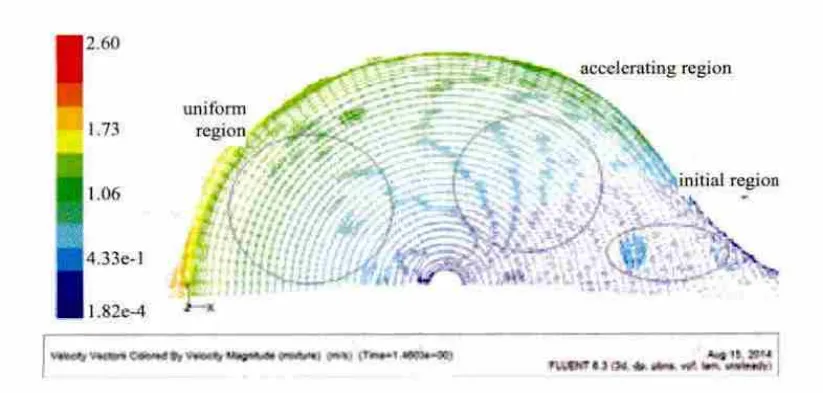
图1 表面液膜速度矢量图谱Fig.1 Liquid film velocity vector of the surface

图2 起始区和加速区速度矢量图谱Fig.2 The velocity vector of initial region and accelerating region
类似于平板抽出模型,在起始区,速度矢量如图2中的下部分,液膜较厚,膜厚方向速度梯度小,部分液体有向下的速度回流到槽里,没有随圆盘转动。如图3,起始阶段速度先减小再增加也是因为部分液体回流,(以VL/VD比值作为纵坐标,VL为液膜表面速度,VD为r为150 mm 处圆盘线速度)。
在加速区,如图2上部分,速度随着角度增加而增加,根据质量守恒,液膜加速,里面的液体暴露出来,表面得以更新。如图3,当θ大于π/2 后,加速度减小,进入匀速区域,匀速区的速度变化较小,液膜速度与半径成正比,与角度无关。
2.1.2 圆盘表面液膜厚度分布
膜厚分布如图4,分别取圆盘表面半径r为50,75,100 mm 局部各点的膜厚,如图5,膜厚在切向随角度的增加而单调减小,表明圆盘抽出时液膜弯月面的存在,与平板抽出模型膜厚随平板高度分布规律一致。另外,膜厚随着半径的增加而增加,当圆盘从液体中抽出时,盘上各点的切线速度与半径成正比,速度越大,圆盘带起的液体越多。起始区和加速区膜厚随半径增加而明显增加,在匀速区膜厚与半径和角度关系较小,基本趋于恒定。

图3 液膜表面速度大小径向和切向分布规律Fig.3 The radial and tangential distribution of liquid film velocity
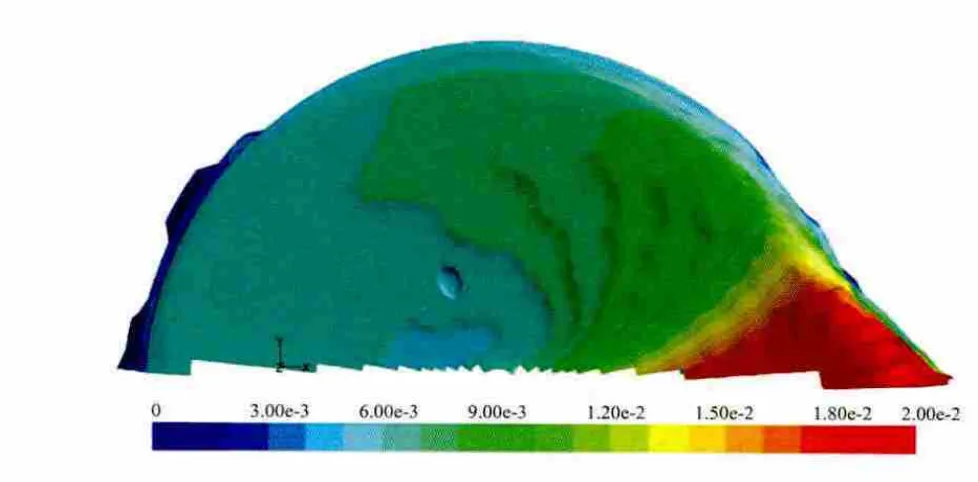
图4 圆盘表面膜厚分布Fig.4 The distribution of film thickness

图5 膜厚径向和切向分布规律Fig.5 The radial and tangential distribution of film thickness
2.1.3 圆盘间距对槽内液相流型的影响
模拟了μ为1 000 mPa·s,N为60 r/min,盘间距L分别为25,35,45,60,80 mm,半径R为75 mm 的两个圆盘之间的流场。
模拟发现,当L为80 mm,槽内流体出现Stewartson 流型(A 流型),如图6所示。Stewartson认为盘两侧均为离心机,流体只在边界层内随盘面旋转,而轴向流动和径向流动均发生在边界层外。从俯视图可以看出,两盘之间的液相区域形成两个涡,涡中心沿竖直方向,称为“垂直涡”,涡中间存在明显的“死区”,流体只在其中做局部循环。图中红色代表液相,蓝色代表气相,如图7,在z为10 mm 平面处的速度矢量图上气液界面水平,两相均存在中心沿水平方向的涡,称为“水平涡”,“水平涡”在液相内形成一个总体循环,更新液相与气液的接触面。这两个漩涡主导槽内流体的运动。因此可以推断在靠近圆盘区域10~20 mm 内液相存在着三维的循环。
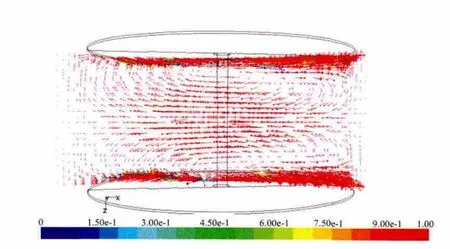
图6 L 为80 mm 速度矢量俯视图谱 (y=-10 mm)Fig.6 The top view of velocity vector (y=-10 mm)
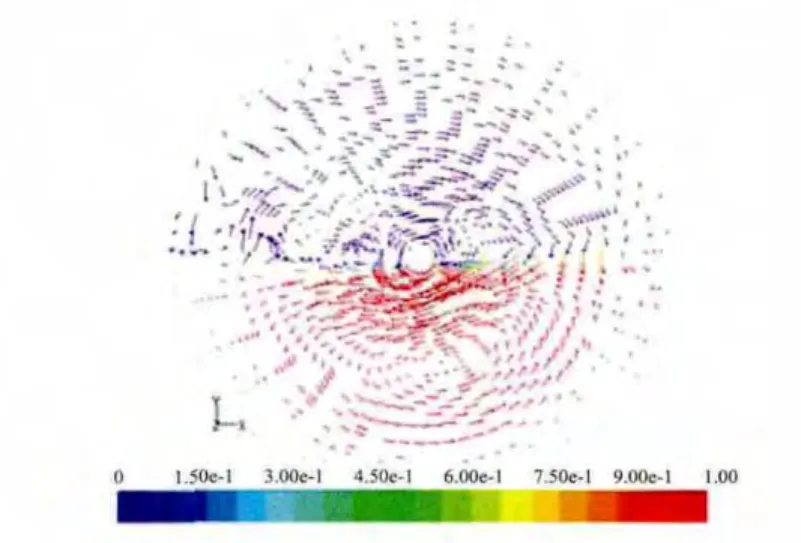
图7 L 为80 mm 速度矢量侧视图谱 (z=10 mm)Fig.7 The side view of velocity vector (z=10 mm)

图8 L 为45 mm 时速度矢量图谱 (y=-10 mm)Fig.8 The top view of velocity vector (y=-10 mm)
当L为45 mm,槽内流体流型如图8所示(B 流型),随着圆盘间距的减小,“垂直涡”被“挤压”,漩涡的中心分别向圆盘靠拢,这是个过渡区域,“垂直涡”依然存在,但是“死区”消失,最有利于混合。
当L为25 mm,随着圆盘间距进一步减小出现如图9所示C 流型,漩涡中心消失,“垂直涡”消失,从z为10 mm 的速度矢量图上可以看出,“水平漩涡”依然存在。如图10,气液界面开始倾斜,随着盘间距的减小,部分液体被夹带到气相,部分气体被夹带到液相。可以推断,盘间距过小,会使两个盘之间液体相连,两个盘合并成一个盘,盘间液体随圆盘一起转动,无法形成有效地更新。
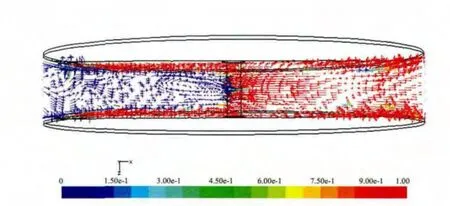
图9 L 为25 mm 时速度矢量图谱 (y=-10 mm)Fig.9 The top view of velocity vector (y=-10 mm)

图10 L 为25 mm 时 速度矢量图谱 (z=10mm)Fig.10 The side view of velocity vector (z=10mm)
总体而言,以上流型都属于Stewartson 流型,只是在不同条件下有一定差别。根据各种流型随盘间距的演变过程分析,认为B 流型可能是最有利于槽体内液相混合。
2.1.4 圆盘与槽体之间的物质交换
Yamane等[18]在1972年最早研究了生物转盘的圆盘表面与槽体之间的物质交换。假设圆盘转动时,盘上液体与釜内液体完全混合,即认为交换更新率为100%,并得到了圆盘的传质速率表达式。Bintanja等[7]对这个假设进行了检验发现,这一假设未必成立。Zeevalkink 等[19]研究发现,一定转速范围内实验测得的传质系数比理论值小50%以上。认为圆盘每旋转一周,仅有25%~50%的液膜被更新,远远低于Yamane 等假设的100%。
本研究先通过三维非稳态VOF 两相流模拟半径均为75 mm 的两个圆盘之间的流场。液体粘度μ为1 000 mPa·s,N为60 r/min,L分别为25,35,45,60,80 mm。流场稳定后,在槽体内均匀加入少量具有同种性质的第三类互溶组分,待圆盘旋转一周后统计圆盘表面第三类组分含量,根据其比例获得液膜旋转一周后被更新的百分率。不同间距圆盘液膜更新率如图11所示。
由图可知,在CFD 模拟的圆盘间距与圆盘直径之比(L/D)范围内,液膜更新率也只有25%~45%,与Zeevalkink 等的研究结果一致,远小于100%。当L/D为0.3 时圆盘表面液膜获得最大的更新百分率。此时处于B 流型,这也与流场分析结果一致。
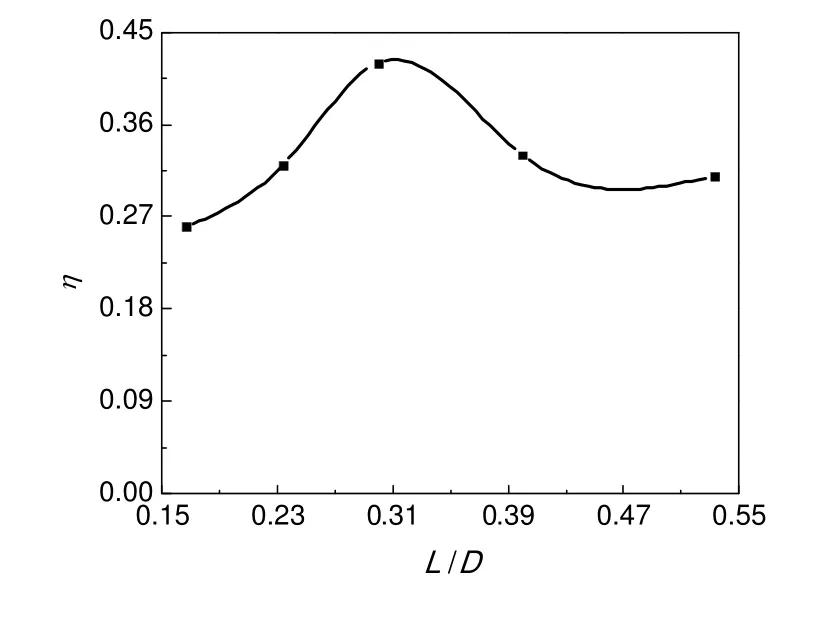
图11 圆盘液膜更新率与间距关系Fig.11 The relationship between liquid renewal and distance of discs
2.2 性能预测
在圆盘反应器的不同应用中,功率特性和持液量都是其基本性能参数,通过CFD 对其进行研究,给出了其估算方法,并探讨了相关影响因素。功率与力矩和转速的关系为:P=Mω
已知力矩即可得知功率,因而获得功率的问题转化为CFD 计算力矩。对液面以上网格进行液相体积积分,能够直接获得圆盘持液量,根据圆盘面积转换成相应的平均膜厚。
2.2.1 圆盘间距对性能的影响
以L/D为横坐标,膜厚和功率随盘间距变化如图12和图13所示。由图可知,膜厚和功率都随着圆盘间距的增加而减小,当L/D大于0.4 时,膜厚和功率基本不变。
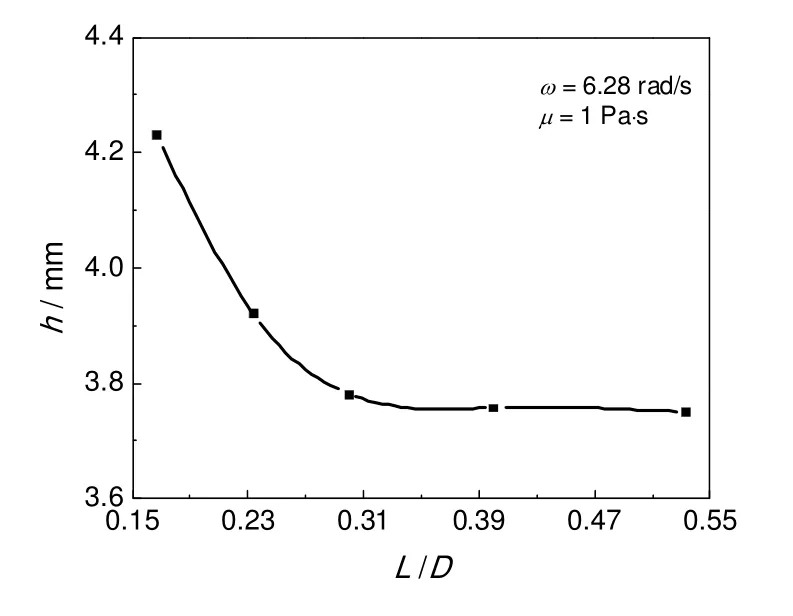
图12 平均膜厚随盘间距的变化规律Fig.12 The law of average film thickness changes with disc spacing
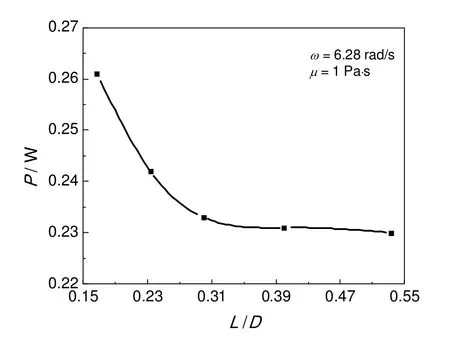
图13 功率随圆盘间距的变化规律Fig.13 The law of power changes with disc spacing
2.2.2 槽体壁效应对性能的影响
改变圆盘与槽体间距d,进行模拟计算,圆盘半径为75 mm。壁效应是筒体对圆盘性能的影响,与圆盘和筒体间距有关,也与圆盘性能有关,膜厚是性能的重要体现,当间距一定时,膜厚越厚,壁效应也会越明显。因此以d/h为横坐标无量纲化。模拟结果以间距d/h为横坐标,示于图14和图15。由图可得,膜厚随着圆盘与筒体间距的增加而增加,功率则减小。当圆盘与筒体间距d/h大于10 时,圆筒的壁效应可以忽略。可见壁效应对于膜厚和功率的影响是同步的,但效应相反。

图14 壁效应对膜厚的影响Fig.14 The influence of wall effect on film thickness

图15 壁效应对功率的影响Fig.15 The influence of wall effect on power
2.2.3 圆盘功率特性
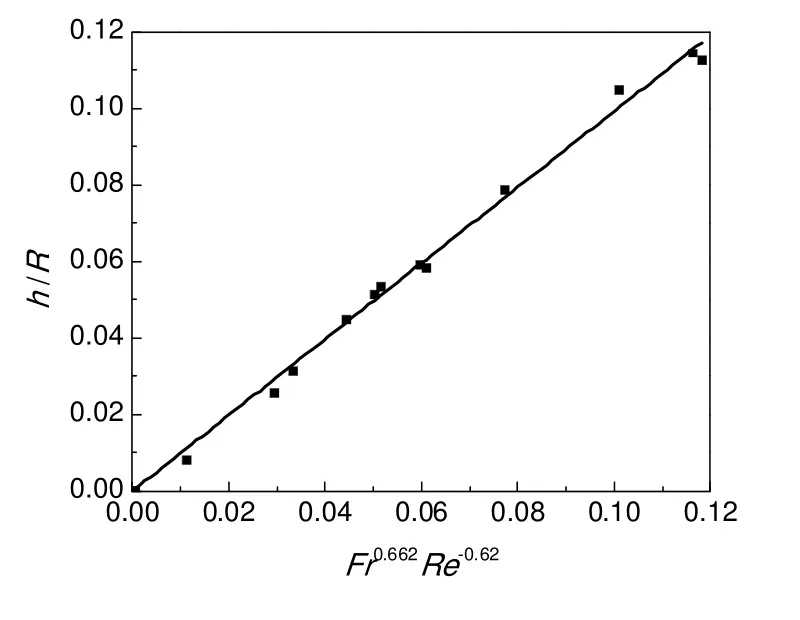
根据CFD 计算得到的功率进行数据关联,线性拟合得到:P∝R3.19,P∝ω1.97。假设:NP=βRem(Fr/Re)n,通过P与R和ω量纲分析得到:m=-0.95,n=-0.09。线性拟合如图16所示。因此,NP=6.81Re-0.95(Fr/Re)-0.09。其中:0 图16 功率数线性拟合Fig.16 Linear fitting of power number 图17 平均膜厚拟合Fig.17 Linear fitting of average film thickness 2.2.4 圆盘持液量特性 根据CFD 计算得到的平均膜厚进行数据关联,线性拟合得到:h∝R0.441,h∝ω0.731,h∝μ0.517。假设h/R为kFraReb,其中k为比例系数,通过量纲分析得到:a=0.662,b=-0.610。将h/R与Fr0.662Re-0.610线性拟合,如图17所示。因此k为1,即:h/R=Fr0.662Re-0.610。其中:0 图18 不同文献平均膜厚对比Fig.18 The comparison of average film thickness with different literature 与文献报道的关联式进行对比,以CFD 计算得到的h/R值作为横坐标,以相应条件下通过文献公式计算得到的h/R值作为纵坐标作图,结果如图18所示。由图可知,通过CFD 计算得到的膜厚刚好分布在对角线上,不同文献得到的数值与其比较。1942年Levich 平板抽出模型得到的膜厚最大,在对角线上方,由于没有考虑重力因素,膜厚明显增加,另外平板抽出模型与圆盘旋转的流体受力和流动行为有一定差异。在转速较低、膜厚较薄时,本研究得到的关联式与Zhevalkink[8]的关联式计算结果是一致的,但随着转速和粘度增加,膜厚变厚,两者的差异增大,主要原因是Zhevalkink 实验条件下Fr小于0.4,忽略了离心力和惯性力的作用,随着转速和粘度增加,这些因素的影响也趋于明显。 运用CFD 方法,通过VOF 模型研究圆盘反应器流场特性和主要性能,所得结论如下: a)圆盘表面分为起始区,加速区和匀速区三个部分。起始区内液膜较厚,不同位置膜厚变化大,液膜速度较低,部分液体回流,存在速度为零的驻点。加速区膜厚变化大,液膜加速,内层的液体暴露出来,更新较快。匀速区液膜厚度最薄,速度最大,但是两者变化较小。 b)圆盘反应器釜内液相主体呈现Stewartson 流型,由“垂直涡”和“水平涡”主导,受圆盘间距影响明显,随着盘间距的减小“垂直涡”相互挤压,“死区”消失,当盘间距进一步减小时,液相和气相夹带严重,不能正常操作。“垂直涡”是槽体与圆盘进行物质交换的主要方式。计算表明,圆盘适宜间距:0.2 c)通过量纲分析和数值模拟得到圆盘反应器的功率数: d)平均膜厚表达式: 适用于更广泛的操作范围和物系范围。 符号说明 Ca——Capillary 数,Ca=μωR/σ D——圆盘直径,mm Fr——Froude 数,Fr=ω2R/g h——液膜厚度,mm h∞——恒定膜厚,mm H——液位到圆盘中心的距离,mm L——圆盘间距,mm r——某点位置半径,mm R——圆盘半径,mm Re——雷诺数,Re=ρω2R/μ T——无量纲膜厚 u——速度矢量,m/s α——相体积分率 η——液相更新率 μ——液体粘度,mPa·s ω——圆盘转速,rad/s [1]Li K, Yang C, Xu Y, et al.Effect of inorganic anions on Rhodamine B removal under visible light irradiation using Bi2O3/Ti rotating disk reactor [J].Chemical Engineering Journal, 2012, 211:208-215. [2]Sakurai A, Imai H, Takenaka Y, et al.Simulation of citric acid production by rotating disk contactor [J].Biotechnology and Bioengineering, 1997, 56(6):689-696. [3]Vasiliadou I A, Molina R, Martínez F, et al.Experimental and modeling study on removal of pharmaceutically active compounds in rotating biological contactors [J].Journal of Hazardous Materials, 2014, 274:473-482. [4]Landau L, Levich B.Dragging of a liquid by a moving plate [J].Acta Physico-Chemica USSR, 1942, 17:42-54. [5]White D A, Tallmadge J A.Theory of drag out of liquids on flat plates [J].Chemical Engineering Science, 1965, 20(1):33-37. [6]Groenveld P.Dip-coating by withdrawal of liquid films [D].Delft:Delft University, 1970. [7]Bintanja H H J, van der Erve J J V M, Boelhouwer C.Oxygen transfer in a rotating disc treatment plant [J].Water Research, 1975,9(12):1147-1153. [8]Zhevalkink J A, Kelderman P, Boelhouwer C.Liquid film thickness in a rotating disc gas-liquid contactor [J].Water Research, 1978,12(8):577-581. [9]Vijayraghvan K, Gupta J P.Thickness of the film formed on a vertically rotating disk partially immersed in a Newtonian liquid [J].Industrial &Engineering Chemistry Fundamentals, 1982, 21(4):333-336. [10]Afanasiev K, Münch A, Wagner B.Thin film dynamics on a vertically rotating disk partially immersed in a liquid bath [J].Applied Mathematical Modelling, 2008, 32(9):1894-1911. [11]杨晓宇, 李志鹏, 高正明.圆盘反应器内流动和成膜性能的数值模拟 [J].北京化工大学学报:自然科学版, 2010, 37(6):29-34.Yang Xiaoyu, Li Zhipeng, Gao Zhengming.Numerical simulation of the flow and film-forming characteristics in a horizontal rotating disk reactor [J].Journal of Beijing University of Chemical Technology, 2010, 37(6):29-34. [12]Batchelor G K.Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow [J].The Quarterly Journal of Mechanics and Applied Mathematics, 1951, 4(1):29-41. [13]Stewartson K.On the flow between two rotating coaxial disks[C]//Proc.Camb.Phil.Soc.1953, 49(2):333-341. [14]王良生, 周贤爵.圆盘反应器的混合特性 [J].高校化学工程学报, 2000, 14(1):37-42.Wang Liangsheng, Zhou Xianjue.The research of mixing characteristic in disc-ring reactor [J].Journal of Chemical Engineering of Chinese Universities, 2000, 14(1):37-42. [15]Fujie K, Bravo H E, Kubota H.Operational design and power economy of a rotating biological contactor [J].Water Research, 1983,17(9):1153-1162. [16]Hirt C W, Nichols B D.Volume of fluid (VOF) method for the dynamics of free boundaries [J].Journal of Computational Physics, 1981,39(1):201-225. [17]邓 斌, 戴干策.圆盘反应器液膜表面更新数值模拟 [J].化工学报, 2015, 66(4):1407-1416.Deng Bin, Dai Gance.Numerical simulation of surface renewal frequency on vertically rotating disc [J].Journal of Chemical Industry and Engineering, 2015, 66(4):1407-1416. [18]Yamane T, Yoshida F.Absorption in a rotating-disk gas-liquid contactor [J].Journal of Chemical Engineering of Japan, 1972,5(4):381-385. [19]Zeevalkink J A, Kelderman P, Visser D C, et al.Physical mass transfer in a rotating disc gas-liquid contactor [J].Water Research, 1979,13(9):913-919.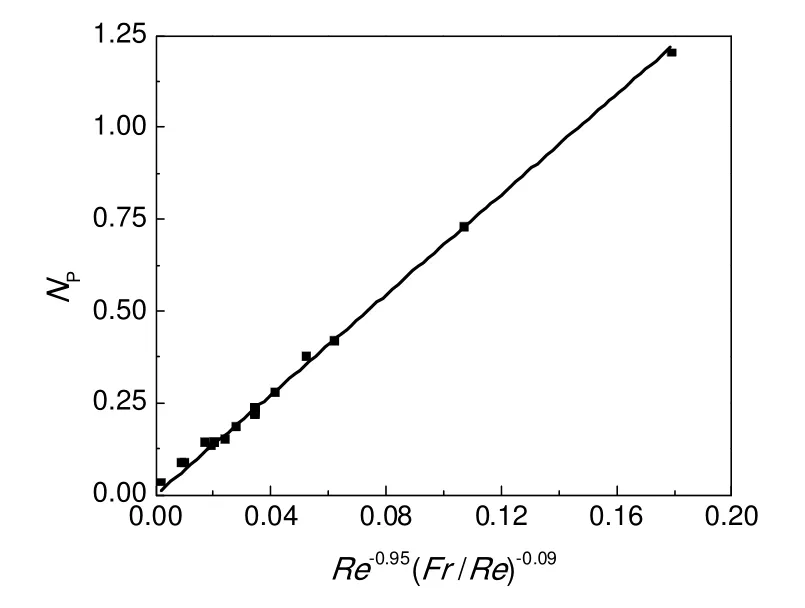

3 结 论


