一类传染病模型的动力学分析
2015-11-17李艳红
李艳红
(昆明理工大学城市学院,云南昆明 650051)
一类传染病模型的动力学分析
李艳红
(昆明理工大学城市学院,云南昆明 650051)
传染病是危害人类身体健康的重要病症之一,长期以来人类的生存和经济的发展都深受其害.通过阅读相关文献发现,目前对传染病的研究基本是进行数据拟合来预测病情趋势,却很少考虑当时间变化时怎样更好的控制传染病.为了更接近现实医学,本文首先建立了包含接种者和隔离者的SVEIQR模型,从而找到基本再生数,然后通过参数的设置和控制,达到控制并最终消除传染病的目的.
传染病;接种;隔离;基本再生数;稳定性
1 引言
当传染病具备传染源、传播途径、易感人群等条件时,就会在人群中传播,但会受到自然因素和社会因素的影响.目前医学上较有效且常用的措施分别是隔离治疗已患病者和预防(如接种疫苗)易感染者.因此找到一个最优疫苗接种和隔离控制策略来阻止传染病的蔓延具有十分重要的意义.
2 预备知识及相关理论
2.1 线性稳定性
考虑具有常系数的线性系统

其中A=(aij)n×n是n阶实矩阵,x∈!n
定理2.1(1)系统(2.1)具有稳定的平凡解⇔矩阵A的特征值都具有负实部或零实部,且具有零实部的特征值仅仅对应矩阵A的简单初等因子.
(2)系统(2.1)的平凡解是渐进稳定的⇔矩阵A的所有特征值的实部均小于零.
(3)系统(2.1)的平凡解是不稳定的⇔矩阵A存在具有正实部的特征值或存在对应于多重初等因子的零实部特征值.
2.2 线性系统的扰动理论
设非线性系统

考虑F对x的Jacobi矩阵
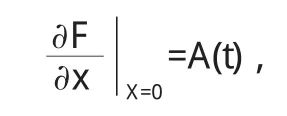
若它与t无关,则系统(2.2)可以写成

其中f(t,x)∈C[I×in,in],f(t,0)=0.
定理2.2设f(t,x)在[t0,+∞]×in上连续,关于x满足Lipschitz条件,且对t一致有
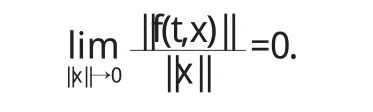
则当A不存在零实部的特征值时,线性系统(2.3)与非线性系统(2.1)具有相同的稳定性.
定理2.3设ζ是in中的有界闭集,从ζ内出发的式(2.1)的解x(t)≡x(t;t0,x0)永远停留在ζ中.若存在V(x)∈C1[ζ,i]使

设S是M内的最大正向不变集,则有

特别的,若S={0}时,式(2.1)的平凡解是渐近稳定的.
3 模型的建立
3.1 模型的建立
由于接种和隔离在传染病控制中的作用越来越明显,因此本文同时考虑了接种和隔离,建立了SVEIQR模型.模型如下:

其中参数如下:
S(t):t时刻易感者的数量p:预防接种率
V(t):t时刻接种者的数量ε:潜伏者向患病者的转化率
E(t):t时刻潜伏者的数量ρ:疾病恢复率
I(t):t时刻患病者的数量d:自然死亡率
Q(t):t时刻隔离者的数量α:因病死亡率
R(t):t时刻恢复者的数量γ:接种者的免疫丧失率
A人口的常数输入率δ:患病者的隔离率
从对限时训练剩余题目处理情况的问卷调查数据发现,69.02%的学生面对限时训练剩下的做错题目想老师去解决,也看出了学生整体知识和能力还是不够,虽然我们给出了详细的解题过程,但是依然无法自己突破,也看出了课后小组成员的交流还不够。
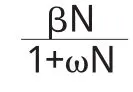
其中αβ(0≤σ≤1)表示接种者的传染率系数,当σ=0时意味着接种者对疾病完全免疫,当σ=1时意味着疫苗完全失效,不具有预防功能.为了更好的模拟实际情况,文中假设接种者具有部分免疫,即0<σ<1;易感者的传染率为饱和型βN/(1+ωN).
3.2 模型的分析
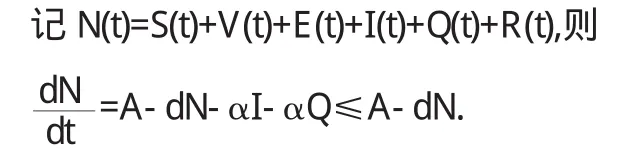
再由(3.1)的第四、五、六个方程知
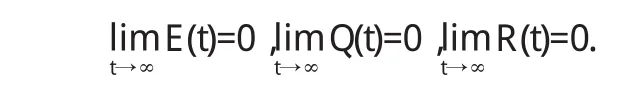
由(3.1)的第一、二个方程可知
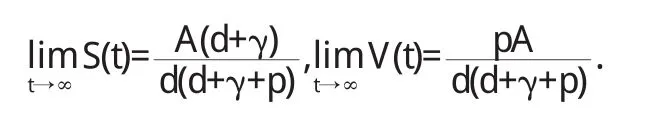
因此(3.1)的全部解(S,V,E,I,Q,R)最终将趋向、进入或停留在区域

3.3 平衡点的存在性
因为模型(3.1)中的前四个方程不含变量Q和A,故考虑如下子系统

类似于前述可得区域
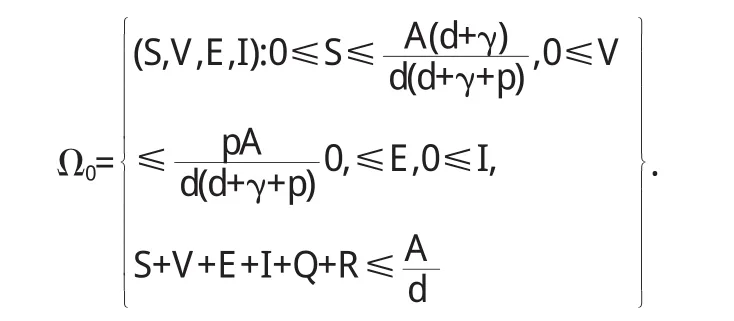
是系统(3.2)的正向不变集.我们以下的讨论均在Ω0内.
当R0≤1时(3.2)仅有无病平衡点M0(S0,V0,E0,I0),其中
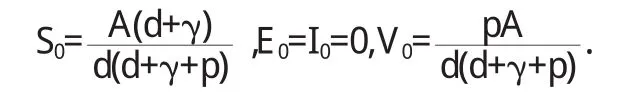
当R0≥1时(3.2)有两个平衡点:无病平衡点M0和地方病平衡点M*(S*,V*,E*,I*),其中

且I*是方程F(I)=0的正根.
定理3.2若R0≤1,具有全局渐近稳定的无病平衡点; 若R0>1,无病平衡点不稳定,地方病平衡点全局渐近稳定.
4 模型的参数控制与主要结果
4.1 对系统(3.2)施加输入控制
设输入控制率为k,则模型变为
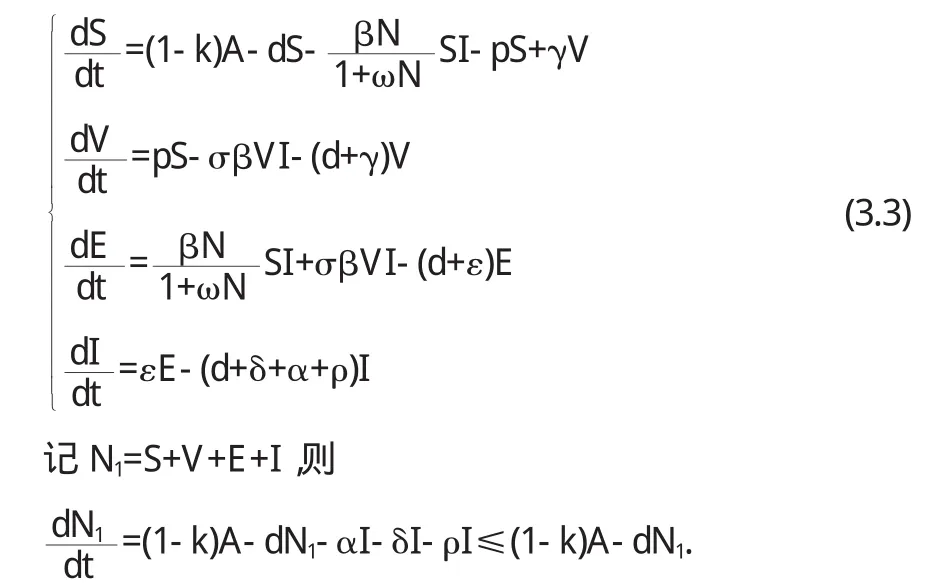
同前面可得

是系统(3.3)的正向不变集.
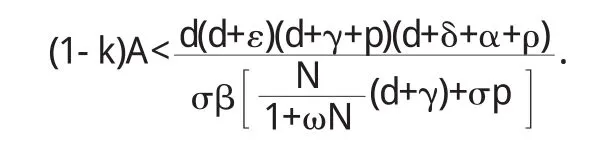
4.2 对系统(3.2)的易感者施加隔离控制
设隔离控制率为m,则模型变为

此时对应的正向不变集仍为Ω0.
定理3.4当
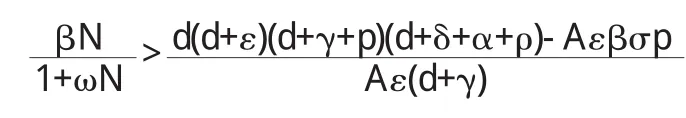

结果:要达到消除传染病的目的,易感者的隔离控制率m要满足
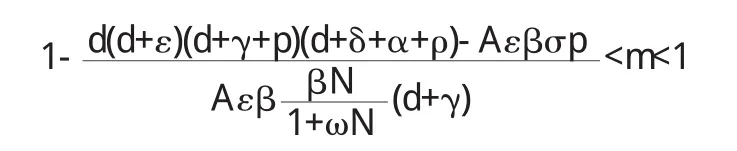
4.3 对系统(3.2)的传染者施加隔离控制
设隔离控制率为n,则模型变为
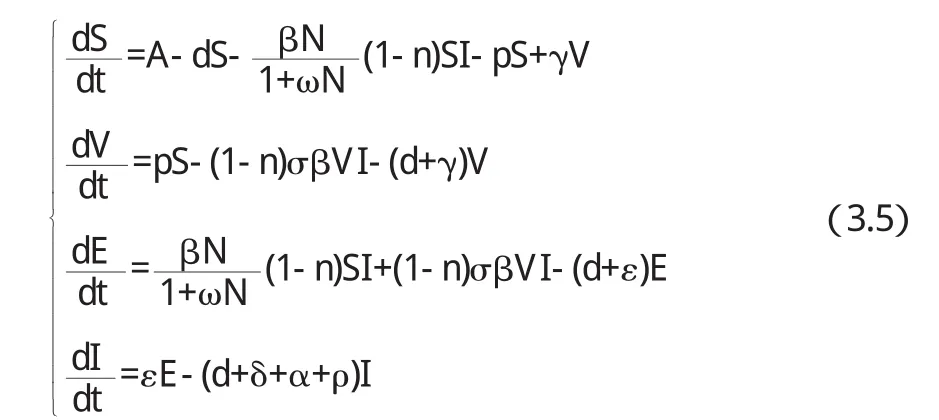

结果:要达到消除传染病的目的,传染病的隔离控制率n要满足

结论:本文通过对非线性传染病的SVEIQR模型的全局分析,找到了决定系统在可行域内动力学行为的重要指标——基本再生数R0,它可控制疾病流行与消除.当R0<1 时,新感染者数量下降,传染病的传播得到控制并最终消除; 当R0>1时,传染病在种群中持续传播蔓延并成为地方病.同时探讨了通过一些控制措施使得基本再生数R0变小,例如控制人口的输入、减少易感者或患病者的人数等,并且可知当参数满足一定的条件时R0<1,从而使得疾病最终消除.
〔1〕余风高.流行病[M].济南:山东画报出版社,2003.
〔2〕马之恩,周义仓,王稳地.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.1-27.
〔3〕Kermack W O,Mckendrick A G.Contributions to the Mathematical Theory of Epidemics[J].Proc.Roy.Soc,1927,(A115):700-721.
〔4〕Hethcote HW,Waltman P.Optimal Vaccination Schedules in a Deterministic Epidemic Model[J].Mathematical Biosciences,1973,18(3-4):365-381.
〔5〕蔡全才,姜庆五,徐勤丰.定量评价SARS干预措施效果的传播动力学模型[J].中华流行病杂志,2005,26(3):153-158.
〔6〕Song X Y,Chen L S.Optimal Harvesting and Stability foraTwo-speciesCompetitiveSystemwithStage Structure[J].Mathematical Biosciences,2001,170:173-186.
〔7〕KunalChakraborty,MilonChakraborty,T.k.kav.Optimal Control of Harvest and Bifurcation of a Prey-predator Model with Stage Structure.Applied Mathematics and Computation,2011,217:8778-8792.
〔8〕Belbas S A,Schmidt W H.Optimal Control of Volterra Equations with Impulses[J]. AppliedMathematicsandComputation,2005,166:696-723.
〔9〕Belbas S A,Schmidt W H.Optimal Control of Volterra EquationswithVariableImpulseTimes[J].Applied Mathematics and Computation,2009,214:353-369.
〔10〕雍炯敏,楼红卫.最优控制理论简明教程[M].北京:高等教育出版社,2006.
O175.1
A
1673-260X(2015)04-0003-03
